Buffered probability of exceedance
Buffered probability of exceedance (bPOE) is a function of a random variable used in statistics and risk management, including financial risk. The bPOE is the probability of a tail with known mean value [math]\displaystyle{ x }[/math]. The figure shows the bPOE at threshold [math]\displaystyle{ x }[/math] (marked in red) as the blue shaded area. Therefore, by definition, bPOE is equal to one minus the confidence level at which the Conditional Value at Risk (CVaR) is equal to [math]\displaystyle{ x }[/math]. bPOE is similar to the probability of exceedance of the threshold [math]\displaystyle{ x }[/math], but the tail is defined by its mean rather than the lowest point [math]\displaystyle{ x }[/math] of the tail.
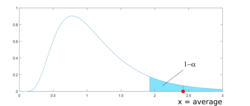
bPOE has its origins in the concept of buffered probability of failure (bPOF), developed by R. Tyrrell Rockafellar and Johannes Royset to measure failure risk.[1] It was further developed and defined as the inverse CVaR by Matthew Norton, Stan Uryasev, and Alexander Mafusalov.[2][3] Similar to CVaR, bPOE considers not only the probability that outcomes (losses) exceed the threshold [math]\displaystyle{ x }[/math], but also the magnitude of these outcomes (losses).[4]
Formal definition
There are two slightly different definitions of bPOE, so called Lower bPOE and Upper bPOE.
For a random variable, [math]\displaystyle{ X }[/math] the Lower bPOE,[2][3] [math]\displaystyle{ \bar{p}_x(X) }[/math], at threshold [math]\displaystyle{ x \in [E[X], \sup X ] }[/math] is given by:
[math]\displaystyle{ \bar{p}_x (X) = \min_{a \geq 0} E[ a(X-x) +1 ]^+ = \min_{\gamma \lt x} \frac{ E[X - \gamma]^+ } { x - \gamma} }[/math]
where [math]\displaystyle{ [\cdot]^+ = \max\{\cdot , 0\} }[/math].
bPOE[3] can be expressed as the inverse function of CVaR:
[math]\displaystyle{ \bar{p}_x (X) = \{ 1 - \alpha | \bar{q}_\alpha (X) = x \} }[/math],
where [math]\displaystyle{ \bar{q}_\alpha (X) }[/math] is the CVaR of [math]\displaystyle{ X }[/math] with confidence level [math]\displaystyle{ \alpha }[/math].
References
- ↑ Rockafellar, R. Tyrrell; Royset, Johannes (2010). "On Buffered Failure Probability in Design and Optimization of Structures". Reliability Engineering and System Safety 95 (5): 499–510. doi:10.1016/j.ress.2010.01.001. https://sites.math.washington.edu/~rtr/papers/rtr211-BufferedProb.pdf.
- ↑ 2.0 2.1 Norton, Matthew; Uryasev, Stan (2018). "Maximization of AUC and Buffered AUC in binary classification". Mathematical Programming (Springer) 174 (1–2): 575–612. doi:10.1007/s10107-018-1312-2. http://uryasev.ams.stonybrook.edu/wp-content/uploads/2018/07/Maximization-of-AUC-and-Buffered-AUC-in-binary-classification.pdf. Retrieved 2023-03-12.
- ↑ 3.0 3.1 3.2 Mafusalov, Alexander; Uryasev, Stan (2018). "Buffered Probability of Exceedance: Mathematical Properties and Optimization". SIAM Journal on Optimization 95 (5): 1077–1103. doi:10.1137/15M1042644. http://uryasev.ams.stonybrook.edu/wp-content/uploads/2018/05/Buffered_probability_of_exceedance.pdf.
- ↑ Norton, Matthew; Khokhlov, Valentyn; Uryasev, Stan (2019). "Calculating CVaR and bPOE for common probability distributions with application to portfolio optimization and density estimation". Annals of Operations Research (Springer) 299 (1–2): 1281–1315. doi:10.1007/s10479-019-03373-1. http://uryasev.ams.stonybrook.edu/wp-content/uploads/2019/10/Norton2019_CVaR_bPOE.pdf. Retrieved 2023-02-27.
 |  |
