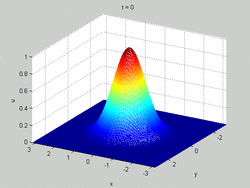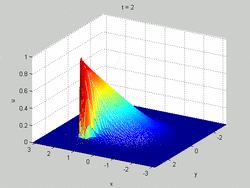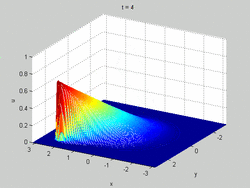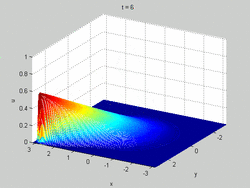
Burgers' equation

From HandWiki
Short description: Partial differential equation

Burgers' equation or Bateman–Burgers equation is a fundamental partial differential equation and convection–diffusion equation[1] occurring in various areas of applied mathematics, such as fluid mechanics,[2] nonlinear acoustics,[3] gas dynamics, and traffic flow.[4] The equation was first introduced by Harry Bateman in 1915[5][6] and later studied by Johannes Martinus Burgers in 1948.[7]

For a given field [math]\displaystyle{ u(x,t) }[/math] and diffusion coefficient (or kinematic viscosity, as in the original fluid mechanical context) [math]\displaystyle{ \nu }[/math], the general form of Burgers' equation (also known as viscous Burgers' equation) in one space dimension is the dissipative system: [math]\displaystyle{ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu\frac{\partial^2 u}{\partial x^2}. }[/math]

When the diffusion term is absent (i.e. [math]\displaystyle{ \nu=0 }[/math]), Burgers' equation becomes the inviscid Burgers' equation: [math]\displaystyle{ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0, }[/math] which is a prototype for conservation equations that can develop discontinuities (shock waves). The previous equation is the advective form of the Burgers' equation. The conservative form is found to be more useful in numerical integration [math]\displaystyle{ \frac{\partial u}{\partial t} + \frac{1}{2}\frac{\partial(u^2)}{\partial x} = 0. }[/math]

Terms

There are 4 parameters in Burgers' equation: [math]\displaystyle{ u, x, t }[/math] and [math]\displaystyle{ \nu }[/math]. In a system consisting of a moving viscous fluid with one spatial ([math]\displaystyle{ x }[/math]) and one temporal ([math]\displaystyle{ t }[/math]) dimension, e.g. a thin ideal pipe with fluid running through it, Burgers' equation describes the speed of the fluid at each location along the pipe as time progresses. The terms of the equation represent the following quantities:[8]

  • [math]\displaystyle{ x }[/math]: spatial coordinate
  • [math]\displaystyle{ t }[/math]: temporal coordinate
  • [math]\displaystyle{ u(x,t) }[/math]: speed of fluid at the indicated spatial and temporal coordinates
  • [math]\displaystyle{ \nu }[/math]: viscosity of fluid

The viscosity is a constant physical property of the fluid, and the other parameters represent the dynamics contingent on that viscosity.

Inviscid Burgers' equation

This is a numerical simulation of the inviscid Burgers Equation in two space variables up until the time of shock formation.

The inviscid Burgers' equation is a conservation equation, more generally a first order quasilinear hyperbolic equation. The solution to the equation and along with the initial condition [math]\displaystyle{ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0, \quad u(x,0) = f(x) }[/math] can be constructed by the method of characteristics. The characteristic equations are [math]\displaystyle{ \frac{dx}{dt} = u, \quad \frac{du}{dt}=0. }[/math]

Integration of the second equation tells us that [math]\displaystyle{ u }[/math] is constant along the characteristic and integration of the first equation shows that the characteristics are straight lines, i.e., [math]\displaystyle{ u=c, \quad x = ut + \xi }[/math] where [math]\displaystyle{ \xi }[/math] is the point (or parameter) on the x-axis (t = 0) of the x-t plane from which the characteristic curve is drawn. Since [math]\displaystyle{ u }[/math] at [math]\displaystyle{ x }[/math]-axis is known from the initial condition and the fact that [math]\displaystyle{ u }[/math] is unchanged as we move along the characteristic emanating from each point [math]\displaystyle{ x=\xi }[/math], we write [math]\displaystyle{ u=c=f(\xi) }[/math] on each characteristic. Therefore, the family of trajectories of characteristics parametrized by [math]\displaystyle{ \xi }[/math] is [math]\displaystyle{ x=f(\xi) t+ \xi. }[/math]

Thus, the solution is given by [math]\displaystyle{ u(x,t) = f(\xi) = f(x-ut), \quad \xi = x - f(\xi) t. }[/math]

This is an implicit relation that determines the solution of the inviscid Burgers' equation provided characteristics don't intersect. If the characteristics do intersect, then a classical solution to the PDE does not exist and leads to the formation of a shock wave. Whether characteristics can intersect or not depends on the initial condition. In fact, the breaking time before a shock wave can be formed is given by[9] [math]\displaystyle{ t_b = \inf_x\left(\frac{-1}{ f'(x)}\right) }[/math]

Inviscid Burgers' equation for linear initial condition

Subrahmanyan Chandrasekhar provided the explicit solution in 1943 when the initial condition is linear, i.e., [math]\displaystyle{ f(x) = ax + b }[/math], where a and b are constants.[10] The explicit solution is [math]\displaystyle{ u(x,t) = \frac{ax+b}{at+1}. }[/math]

This solution is also the complete integral of the inviscid Burgers' equation because it contains as many arbitrary constants as the number of independent variables appearing in the equation.[11][better source needed] Using this complete integral, Chandrasekhar obtained the general solution described for arbitrary initial conditions from the envelope of the complete integral.

Viscous Burgers' equation

This is a numerical solution of the viscous two dimensional Burgers equation using an initial Gaussian profile. We see shock formation, and dissipation of the shock due to viscosity as it travels.

The viscous Burgers' equation can be converted to a linear equation by the Cole–Hopf transformation,[12][13][14] [math]\displaystyle{ u = -2\nu \frac{1}{\phi}\frac{\partial\phi}{\partial x}, }[/math] which turns it into the equation [math]\displaystyle{ \frac{\partial}{\partial x} \left( \frac{1}{\phi}\frac{\partial\phi}{\partial t}\right) = \nu \frac{\partial}{\partial x} \left( \frac{1}{\phi}\frac{\partial^2\phi}{\partial x^2}\right) }[/math] which can be integrated with respect to [math]\displaystyle{ x }[/math] to obtain [math]\displaystyle{ \frac{\partial\phi}{\partial t} = \nu \frac{\partial^2\phi}{\partial x^2} + g(t) \phi }[/math] where [math]\displaystyle{ g(t) }[/math] is a function that depends on boundary conditions. If [math]\displaystyle{ g(t)=0 }[/math] identically (e.g. if the problem is to be solved on a periodic domain), then we get the diffusion equation [math]\displaystyle{ \frac{\partial\phi}{\partial t}=\nu\frac{\partial^2\phi}{\partial x^2}. }[/math]

The diffusion equation can be solved, and the Cole–Hopf transformation inverted, to obtain the solution to the Burgers' equation: [math]\displaystyle{ u(x,t)=-2\nu\frac{\partial}{\partial x}\ln\left\{(4\pi \nu t)^{-1/2}\int_{-\infty}^\infty \exp\left[-\frac{(x-x')^2}{4\nu t} - \frac{1}{2\nu}\int_0^{x'}f(x'')dx''\right]dx'\right\}. }[/math]

Other forms

Generalized Burgers' equation

The generalized Burgers' equation extends the quasilinear convective to more generalized form, i.e., [math]\displaystyle{ \frac{\partial u}{\partial t} + c(u) \frac{\partial u}{\partial x} = \nu\frac{\partial^2 u}{\partial x^2}. }[/math] where [math]\displaystyle{ c(u) }[/math] is any arbitrary function of u. The inviscid [math]\displaystyle{ \nu=0 }[/math] equation is still a quasilinear hyperbolic equation for [math]\displaystyle{ c(u)\gt 0 }[/math] and its solution can be constructed using method of characteristics as before.[15]

Stochastic Burgers' equation

Added space-time noise [math]\displaystyle{ \eta(x,t) = \dot W(x,t) }[/math], where [math]\displaystyle{ W }[/math] is an [math]\displaystyle{ L^2(\mathbb R) }[/math] Wiener process, forms a stochastic Burgers' equation[16] [math]\displaystyle{ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \nu \frac{\partial^2 u}{\partial x^2}-\lambda\frac{\partial\eta}{\partial x}. }[/math]

This stochastic PDE is the one-dimensional version of Kardar–Parisi–Zhang equation in a field [math]\displaystyle{ h(x,t) }[/math] upon substituting [math]\displaystyle{ u(x,t)=-\lambda\partial h/\partial x }[/math].

See also

References

  1. ↑ Misra, Souren; Raghurama Rao, S. V.; Bobba, Manoj Kumar (2010-09-01). "Relaxation system based sub-grid scale modelling for large eddy simulation of Burgers' equation". International Journal of Computational Fluid Dynamics 24 (8): 303–315. doi:10.1080/10618562.2010.523518. ISSN 1061-8562. Bibcode: 2010IJCFD..24..303M. https://doi.org/10.1080/10618562.2010.523518. 
  2. ↑ It relates to the Navier–Stokes momentum equation with the pressure term removed Burgers Equation, https://www.uni-muenster.de/Physik.TP/archive/fileadmin/lehre/NumMethoden/WS0910/ScriptPDE/Burgers.pdf : here the variable is the flow speed y=u
  3. ↑ It arises from Westervelt equation with an assumption of strictly forward propagating waves and the use of a coordinate transformation to a retarded time frame: here the variable is the pressure
  4. ↑ Musha, Toshimitsu; Higuchi, Hideyo (1978-05-01). "Traffic Current Fluctuation and the Burgers Equation" (in en). Japanese Journal of Applied Physics 17 (5): 811. doi:10.1143/JJAP.17.811. ISSN 1347-4065. Bibcode: 1978JaJAP..17..811M. https://iopscience.iop.org/article/10.1143/JJAP.17.811/meta. 
  5. ↑ Bateman, H. (1915). "Some recent researches on the motion of fluids". Monthly Weather Review 43 (4): 163–170. doi:10.1175/1520-0493(1915)43<163:SRROTM>2.0.CO;2. Bibcode: 1915MWRv...43..163B. 
  6. ↑ Whitham, G. B. (2011). Linear and nonlinear waves (Vol. 42). John Wiley & Sons.
  7. ↑ Burgers, J. M. (1948). "A Mathematical Model Illustrating the Theory of Turbulence". Advances in Applied Mechanics 1: 171–199. doi:10.1016/S0065-2156(08)70100-5. ISBN 9780123745798. 
  8. ↑ Cameron, Maria. "Notes on Burgers's Equation". https://www.math.umd.edu/~mariakc/burgers.pdf. 
  9. ↑ Olver, Peter J. (2013). Introduction to Partial Differential Equations. Undergraduate Texts in Mathematics. Online: Springer. pp. 37. doi:10.1007/978-3-319-02099-0. ISBN 978-3-319-02098-3. https://link.springer.com/book/10.1007/978-3-319-02099-0. 
  10. ↑ Chandrasekhar, S. (1943). On the decay of plane shock waves (Report). Ballistic Research Laboratories. Report No. 423. 
  11. ↑ Forsyth, A. R. (1903). A Treatise on Differential Equations. London: Macmillan. 
  12. ↑ Cole, Julian (1951). "On a quasi-linear parabolic equation occurring in aerodynamics". Quarterly of Applied Mathematics 9 (3): 225–236. doi:10.1090/qam/42889. 
  13. ↑ Eberhard Hopf (September 1950). "The partial differential equation ut + uux = μuxx". Communications on Pure and Applied Mathematics 3 (3): 201–230. doi:10.1002/cpa.3160030302. 
  14. ↑ Kevorkian, J. (1990). Partial Differential Equations: Analytical Solution Techniques. Belmont: Wadsworth. pp. 31–35. ISBN 0-534-12216-7. 
  15. ↑ Courant, R., & Hilbert, D. Methods of Mathematical Physics. Vol. II.
  16. ↑ Wang, W.; Roberts, A. J. (2015). "Diffusion Approximation for Self-similarity of Stochastic Advection in Burgers' Equation". Communications in Mathematical Physics 333 (3): 1287–1316. doi:10.1007/s00220-014-2117-7. Bibcode: 2015CMaPh.333.1287W. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Burgers%27_equation&oldid=3371556"