Controlled NOT gate
In computer science, the controlled NOT gate (also C-NOT or CNOT), controlled-X gate, controlled-bit-flip gate, Feynman gate or controlled Pauli-X is a quantum logic gate that is an essential component in the construction of a gate-based quantum computer. It can be used to entangle and disentangle Bell states. Any quantum circuit can be simulated to an arbitrary degree of accuracy using a combination of CNOT gates and single qubit rotations.[1][2] The gate is sometimes named after Richard Feynman who developed an early notation for quantum gate diagrams in 1986.[3][4][5]
The CNOT can be expressed in the Pauli basis as:
- [math]\displaystyle{ \mbox{CNOT} = e^{i\frac{\pi}{4}(I_1-Z_1)(I_2-X_2)}= e^{-i\frac{\pi}{4}(I_1-Z_1)(I_2-X_2)}. }[/math]
Being both unitary and Hermitian, CNOT has the property [math]\displaystyle{ e^{i\theta U}=(\cos \theta)I+(i\sin \theta) U }[/math] and [math]\displaystyle{ U =e^{i\frac{\pi}{2}(I-U)}=e^{-i\frac{\pi}{2}(I-U)} }[/math], and is involutory.
The CNOT gate can be further decomposed as products of rotation operator gates and exactly one two qubit interaction gate, for example
- [math]\displaystyle{ \mbox{CNOT} =e^{-i\frac{\pi}{4}}R_{y_1}(-\pi/2)R_{x_1}(-\pi/2)R_{x_2}(-\pi/2)R_{xx}(\pi/2)R_{y_1}(\pi/2). }[/math]
In general, any single qubit unitary gate can be expressed as [math]\displaystyle{ U = e^{iH} }[/math], where H is a Hermitian matrix, and then the controlled U is [math]\displaystyle{ CU = e^{i\frac{1}{2}(I_1-Z_1)H_2} }[/math].
The CNOT gate is also used in classical reversible computing.
Operation
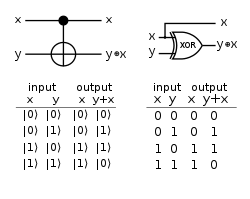
The CNOT gate operates on a quantum register consisting of 2 qubits. The CNOT gate flips the second qubit (the target qubit) if and only if the first qubit (the control qubit) is [math]\displaystyle{ |1\rangle }[/math].
| Before | After | ||
|---|---|---|---|
| Control | Target | Control | Target |
| [math]\displaystyle{ |0\rangle }[/math] | [math]\displaystyle{ |0\rangle }[/math] | [math]\displaystyle{ |0\rangle }[/math] | [math]\displaystyle{ |0\rangle }[/math] |
| [math]\displaystyle{ |0\rangle }[/math] | [math]\displaystyle{ |1\rangle }[/math] | [math]\displaystyle{ |0\rangle }[/math] | [math]\displaystyle{ |1\rangle }[/math] |
| [math]\displaystyle{ |1\rangle }[/math] | [math]\displaystyle{ |0\rangle }[/math] | [math]\displaystyle{ |1\rangle }[/math] | [math]\displaystyle{ |1\rangle }[/math] |
| [math]\displaystyle{ |1\rangle }[/math] | [math]\displaystyle{ |1\rangle }[/math] | [math]\displaystyle{ |1\rangle }[/math] | [math]\displaystyle{ |0\rangle }[/math] |
If [math]\displaystyle{ \{|0\rangle,|1\rangle\} }[/math] are the only allowed input values for both qubits, then the TARGET output of the CNOT gate corresponds to the result of a classical XOR gate. Fixing CONTROL as [math]\displaystyle{ |1\rangle }[/math], the TARGET output of the CNOT gate yields the result of a classical NOT gate.
More generally, the inputs are allowed to be a linear superposition of [math]\displaystyle{ \{|0\rangle,|1\rangle\} }[/math]. The CNOT gate transforms the quantum state:
[math]\displaystyle{ a|00\rangle + b|01\rangle + c|10\rangle + d|11\rangle }[/math]
into:
[math]\displaystyle{ a|00\rangle + b|01\rangle + c|11\rangle + d|10\rangle }[/math]
The action of the CNOT gate can be represented by the matrix (permutation matrix form):
- [math]\displaystyle{ \operatorname{CNOT} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix}. }[/math]
The first experimental realization of a CNOT gate was accomplished in 1995. Here, a single Beryllium ion in a trap was used. The two qubits were encoded into an optical state and into the vibrational state of the ion within the trap. At the time of the experiment, the reliability of the CNOT-operation was measured to be on the order of 90%.[6]
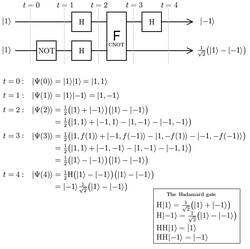
In addition to a regular controlled NOT gate, one could construct a function-controlled NOT gate, which accepts an arbitrary number n+1 of qubits as input, where n+1 is greater than or equal to 2 (a quantum register). This gate flips the last qubit of the register if and only if a built-in function, with the first n qubits as input, returns a 1. The function-controlled NOT gate is an essential element of the Deutsch–Jozsa algorithm.
Behaviour in the Hadamard transformed basis
When viewed only in the computational basis [math]\displaystyle{ \{|0\rangle,|1\rangle\} }[/math], the behaviour of the CNOT appears to be like the equivalent classical gate. However, the simplicity of labelling one qubit the control and the other the target does not reflect the complexity of what happens for most input values of both qubits.
Insight can be won by expressing the CNOT gate with respect to a Hadamard transformed basis [math]\displaystyle{ \{|+\rangle,|-\rangle\} }[/math]. The Hadamard transformed basis[lower-alpha 1] of a one-qubit register is given by
- [math]\displaystyle{ |+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle),\qquad |-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle), }[/math]
and the corresponding basis of a 2-qubit register is
- [math]\displaystyle{ |++\rangle = |+\rangle\otimes|+\rangle = \frac{1}{2}(|0\rangle + |1\rangle)\otimes(|0\rangle + |1\rangle) = \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) }[/math],
etc. Viewing CNOT in this basis, the state of the second qubit remains unchanged, and the state of the first qubit is flipped, according to the state of the second bit. (For details see below.) "Thus, in this basis the sense of which bit is the control bit and which the target bit has reversed. But we have not changed the transformation at all, only the way we are thinking about it."[7]
The "computational" basis [math]\displaystyle{ \{|0\rangle,|1\rangle\} }[/math] is the eigenbasis for the spin in the Z-direction, whereas the Hadamard basis [math]\displaystyle{ \{|+\rangle,|-\rangle\} }[/math] is the eigenbasis for spin in the X-direction. Switching X and Z and qubits 1 and 2, then, recovers the original transformation."[8] This expresses a fundamental symmetry of the CNOT gate.
The observation that both qubits are (equally) affected in a CNOT interaction is of importance when considering information flow in entangled quantum systems.[9]
Details of the computation
We now proceed to give the details of the computation. Working through each of the Hadamard basis states, the first qubit flips between [math]\displaystyle{ |+\rangle }[/math] and [math]\displaystyle{ |-\rangle }[/math] when the second qubit is [math]\displaystyle{ |-\rangle }[/math]:
| Initial state in Hadamard basis | Equivalent state in computational basis | Apply operator | State in computational basis after CNOT | Equivalent state in Hadamard basis |
|---|---|---|---|---|
| [math]\displaystyle{ |++\rangle }[/math] | [math]\displaystyle{ \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) }[/math] | CNOT | [math]\displaystyle{ \frac{1}{2}(|00\rangle + |01\rangle + |11\rangle + |10\rangle) }[/math] | [math]\displaystyle{ |++\rangle }[/math] |
| [math]\displaystyle{ |+-\rangle }[/math] | [math]\displaystyle{ \frac{1}{2}(|00\rangle - |01\rangle + |10\rangle - |11\rangle) }[/math] | CNOT | [math]\displaystyle{ \frac{1}{2}(|00\rangle - |01\rangle + |11\rangle - |10\rangle) }[/math] | [math]\displaystyle{ |--\rangle }[/math] |
| [math]\displaystyle{ |-+\rangle }[/math] | [math]\displaystyle{ \frac{1}{2}(|00\rangle + |01\rangle - |10\rangle - |11\rangle) }[/math] | CNOT | [math]\displaystyle{ \frac{1}{2}(|00\rangle + |01\rangle - |11\rangle - |10\rangle) }[/math] | [math]\displaystyle{ |-+\rangle }[/math] |
| [math]\displaystyle{ |--\rangle }[/math] | [math]\displaystyle{ \frac{1}{2}(|00\rangle - |01\rangle - |10\rangle + |11\rangle) }[/math] | CNOT | [math]\displaystyle{ \frac{1}{2}(|00\rangle - |01\rangle - |11\rangle + |10\rangle) }[/math] | [math]\displaystyle{ |+-\rangle }[/math] |
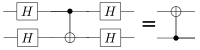
A quantum circuit that performs a Hadamard transform followed by CNOT then another Hadamard transform, can be described as performing the CNOT gate in the Hadamard basis (i.e. a change of basis):
(H1 ⊗ H1)−1 . CNOT . (H1 ⊗ H1)
The single-qubit Hadamard transform, H1, is Hermitian and therefore its own inverse. The tensor product of two Hadamard transforms operating (independently) on two qubits is labelled H2. We can therefore write the matrices as:
H2 . CNOT . H2
When multiplied out, this yields a matrix that swaps the [math]\displaystyle{ |01\rangle }[/math] and [math]\displaystyle{ |11\rangle }[/math] terms over, while leaving the [math]\displaystyle{ |00\rangle }[/math] and [math]\displaystyle{ |10\rangle }[/math] terms alone. This is equivalent to a CNOT gate where qubit 2 is the control qubit and qubit 1 is the target qubit:[lower-alpha 2]
[math]\displaystyle{ \frac{1}{2} \begin{bmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{bmatrix} . \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{bmatrix} . \frac{1}{2} \begin{bmatrix}\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & -1 & 1 & -1\\ 1 & 1 & -1 & -1\\ 1 & -1 & -1 & 1 \end{array}\end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 \end{bmatrix} }[/math]
Constructing a Bell State
A common application of the CNOT gate is to maximally entangle two qubits into the [math]\displaystyle{ |\Phi^+\rangle }[/math] Bell state; this forms part of the setup of the superdense coding, quantum teleportation, and entangled quantum cryptography algorithms.
To construct [math]\displaystyle{ |\Phi^+\rangle }[/math], the inputs A (control) and B (target) to the CNOT gate are:
[math]\displaystyle{ \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)_A }[/math] and [math]\displaystyle{ |0\rangle_B }[/math]
After applying CNOT, the resulting Bell State [math]\displaystyle{ \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) }[/math] has the property that the individual qubits can be measured using any basis and will always present a 50/50 chance of resolving to each state. In effect, the individual qubits are in an undefined state. The correlation between the two qubits is the complete description of the state of the two qubits; if we both choose the same basis to measure both qubits and compare notes, the measurements will perfectly correlate.
When viewed in the computational basis, it appears that qubit A is affecting qubit B. Changing our viewpoint to the Hadamard basis demonstrates that, in a symmetrical way, qubit B is affecting qubit A.
The input state can alternately be viewed as:
[math]\displaystyle{ |+\rangle_A }[/math] and [math]\displaystyle{ \frac{1}{\sqrt{2}}(|+\rangle + |-\rangle)_B }[/math]
In the Hadamard view, the control and target qubits have conceptually swapped and qubit A is inverted when qubit B is [math]\displaystyle{ |-\rangle_B }[/math]. The output state after applying the CNOT gate is [math]\displaystyle{ \frac{1}{\sqrt{2}}(|++\rangle + |--\rangle) }[/math] which can be shown as follows:
[math]\displaystyle{ = \frac{1}{\sqrt{2}}(|+\rangle_A|+\rangle_B + |-\rangle_A|-\rangle_B) }[/math]
[math]\displaystyle{ = \frac{1}{2\sqrt{2}}((|0\rangle_A + |1\rangle_A)(|0\rangle_B + |1\rangle_B) + (|0\rangle_A - |1\rangle_A)(|0\rangle_B - |1\rangle_B)) }[/math]
[math]\displaystyle{ = \frac{1}{2\sqrt{2}}((|00\rangle + |01\rangle + |10\rangle + |11\rangle) + (|00\rangle - |01\rangle - |10\rangle + |11\rangle)) }[/math]
[math]\displaystyle{ = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) }[/math].
C-ROT gate
The C-ROT gate (controlled Rabi rotation) is equivalent to a C-NOT gate except for a [math]\displaystyle{ \pi /2 }[/math] rotation of the nuclear spin around the z axis.[10][11]
Implementations
Trapped ion quantum computers:
See also
- Toffoli gate (controlled-controlled-NOT gate)
Notes
- ↑ Note that [math]\displaystyle{ |+\rangle }[/math] can be constructed by applying a Hadamard gate to a qubit set to [math]\displaystyle{ |0\rangle }[/math], and similarly for [math]\displaystyle{ |-\rangle }[/math]
- ↑ That is, [math]\displaystyle{ H_2 \cdot \operatorname{CNOT} \cdot H_2 = \operatorname{SWAP} \cdot \operatorname{CNOT} \cdot \operatorname{SWAP} }[/math] where [math]\displaystyle{ \operatorname{SWAP} }[/math] is the SWAP gate.
References
- ↑ Barenco, Adriano; Bennett, Charles H.; Cleve, Richard; DiVincenzo, David P.; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A. et al. (1995-11-01). "Elementary gates for quantum computation". Physical Review A (American Physical Society (APS)) 52 (5): 3457–3467. doi:10.1103/physreva.52.3457. ISSN 1050-2947. PMID 9912645. Bibcode: 1995PhRvA..52.3457B.
- ↑ Nielsen, Michael A.; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 0521632358. OCLC 43641333.
- ↑ Feynman, Richard P. (1986). "Quantum mechanical computers" (in en). Foundations of Physics 16 (6): 507–531. doi:10.1007/BF01886518. ISSN 0015-9018. Bibcode: 1986FoPh...16..507F. http://link.springer.com/10.1007/BF01886518.
- ↑ Samrin, S. Saniya; Patil, Rachamma; Itagi, Sumangala; Chetti, Smita C; Tasneem, Afiya (2022-06-01). "Design of logic gates using reversible gates with reduced quantum cost" (in en). Global Transitions Proceedings. International Conference on Intelligent Engineering Approach(ICIEA-2022) 3 (1): 136–141. doi:10.1016/j.gltp.2022.04.011. ISSN 2666-285X. Bibcode: 2022GloTP...3..136S.
- ↑ Thapliyal, Himanshu; Ranganathan, Nagarajan (2009). "Design of Efficient Reversible Binary Subtractors Based on a New Reversible Gate". 2009 IEEE Computer Society Annual Symposium on VLSI. pp. 229–234. doi:10.1109/ISVLSI.2009.49. ISBN 978-1-4244-4408-3. https://ieeexplore.ieee.org/document/5076412.
- ↑ Monroe, C.; Meekhof, D.; King, B.; Itano, W.; Wineland, D. (1995). "Demonstration of a Fundamental Quantum Logic Gate". Physical Review Letters 75 (25): 4714–4717. doi:10.1103/PhysRevLett.75.4714. PMID 10059979. Bibcode: 1995PhRvL..75.4714M.
- ↑ Eleanor G. Rieffel; Wolfgang H. Polak (4 March 2011). Quantum Computing: A Gentle Introduction. Cambridge, Mass.: MIT Press. p. 80. ISBN 978-0-262-01506-6. OCLC 742513505.
- ↑ Gottesman, Daniel (1998). S. P. Corney. ed. "The Heisenberg Representation of Quantum Computers". Group: Proceedings of the XXII International Colloquium on Group Theoretical Methods in Physics (Cambridge, MA: International Press) 22 (1999): 32–43. Bibcode: 1998quant.ph..7006G.
- ↑ Deutsch, David; Hayden, Patrick (1999). "Information Flow in Entangled Quantum Systems". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 456 (1999): 1759–1774. doi:10.1098/rspa.2000.0585. Bibcode: 2000RSPSA.456.1759D.
- ↑ Chen, Pochung; Piermarocchi, C.; Sham, L. J. (18 July 2001). "Control of Exciton Dynamics in Nanodots for Quantum Operations". Physical Review Letters 87 (6): 067401. doi:10.1103/PhysRevLett.87.067401. PMID 11497860. Bibcode: 2001PhRvL..87f7401C.
- ↑ Piermarocchi, C.; Chen, Pochung; Sham, L. J.; Steel, D. G. (30 September 2002). "Optical RKKY Interaction between Charged Semiconductor Quantum Dots". Physical Review Letters 89 (16): 167402. doi:10.1103/PhysRevLett.89.167402. PMID 12398754. Bibcode: 2002PhRvL..89p7402P.
External links
 |  |
