Bell state

Short description: Quantum states of two qubits

In quantum information science, the Bell's states or EPR pairs are specific quantum states of two qubits that represent the simplest examples of quantum entanglement. The Bell's states are a form of entangled and normalized basis vectors. This normalization implies that the overall probability of the particle being in one of the mentioned states is 1: [math]\displaystyle{ \langle \Phi|\Phi \rangle = 1 }[/math]. Entanglement is a basis-independent result of superposition. Due to this superposition, measurement of the qubit will "collapse" it into one of its basis states with a given probability. Because of the entanglement, measurement of one qubit will "collapse" the other qubit to a state whose measurement will yield one of two possible values, where the value depends on which Bell's state the two qubits are in initially. Bell's states can be generalized to certain quantum states of multi-qubit systems, such as the GHZ state for three or more subsystems.

Understanding of Bell's states is useful in analysis of quantum communication, such as superdense coding and quantum teleportation. The no-communication theorem prevents this behavior from transmitting information faster than the speed of light.

Bell states

The Bell states are four specific maximally entangled quantum states of two qubits. They are in a superposition of 0 and 1 – a linear combination of the two states. Their entanglement means the following:

The qubit held by Alice (subscript "A") can be in a superposition of 0 and 1. If Alice measured her qubit in the standard basis, the outcome would be either 0 or 1, each with probability 1/2; if Bob (subscript "B") also measured his qubit, the outcome would be the same as for Alice. Thus, Alice and Bob would each seemingly have random outcome. Through communication they would discover that, although their outcomes separately seemed random, these were perfectly correlated.

This perfect correlation at a distance is special: maybe the two particles "agreed" in advance, when the pair was created (before the qubits were separated), which outcome they would show in case of a measurement.

Hence, following Einstein, Podolsky, and Rosen in their famous 1935 "EPR paper", there is something missing in the description of the qubit pair given above – namely this "agreement", called more formally a hidden variable. In his famous paper of 1964, John S. Bell showed by simple probability theory arguments that these correlations (the one for the 0,1 basis and the one for the +,- basis) cannot both be made perfect by the use of any "pre-agreement" stored in some hidden variables – but that quantum mechanics predicts perfect correlations. In a more refined formulation known as the Bell–CHSH inequality, it is shown that a certain correlation measure cannot exceed the value 2 if one assumes that physics respects the constraints of local "hidden-variable" theory (a sort of common-sense formulation of how information is conveyed), but certain systems permitted in quantum mechanics can attain values as high as [math]\displaystyle{ 2\sqrt{2} }[/math]. Thus, quantum theory violates the Bell inequality and the idea of local "hidden variables."

Bell basis

Four specific two-qubit states with the maximal value of [math]\displaystyle{ 2\sqrt{2} }[/math] are designated as "Bell states". They are known as the four maximally entangled two-qubit Bell states and they form a maximally entangled basis, known as the Bell basis, of the four-dimensional Hilbert space for two qubits:

[math]\displaystyle{ |\Phi^+\rangle = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B + |1\rangle_A \otimes |1\rangle_B) }[/math] (1)

[math]\displaystyle{ |\Phi^-\rangle = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |0\rangle_B - |1\rangle_A \otimes |1\rangle_B) }[/math] (2)

[math]\displaystyle{ |\Psi^+\rangle = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B + |1\rangle_A \otimes |0\rangle_B) }[/math] (3)

[math]\displaystyle{ |\Psi^-\rangle = \frac{1}{\sqrt{2}} (|0\rangle_A \otimes |1\rangle_B - |1\rangle_A \otimes |0\rangle_B) }[/math] (4)

Creating Bell states via quantum circuits

Quantum circuit to create Bell state [math]\displaystyle{ |\Phi^+\rangle }[/math].

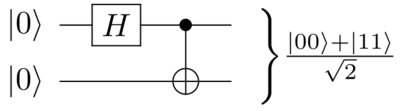
Although there are many possible ways to create entangled Bell states through quantum circuits, the simplest takes a computational basis as the input, and contains a Hadamard gate and a CNOT gate (see picture). As an example, the pictured quantum circuit takes the two qubit input [math]\displaystyle{ |00\rangle }[/math] and transforms it to the first Bell state [math]\displaystyle{ |\Phi^+\rangle. }[/math] Explicitly, the Hadamard gate transforms [math]\displaystyle{ |00\rangle }[/math] into a superposition of [math]\displaystyle{ (|0\rangle|0\rangle + |1\rangle|0\rangle) \over \sqrt{2} }[/math]. This will then act as a control input to the CNOT gate, which only inverts the target (the second qubit) when the control (the first qubit) is 1. Thus, the CNOT gate transforms the second qubit as follows [math]\displaystyle{ \frac{(|00\rangle + |11\rangle)}{\sqrt{2} } = |\Phi^+\rangle }[/math].

For the four basic two-qubit inputs, [math]\displaystyle{ |00\rangle, |01\rangle, |10\rangle, |11\rangle }[/math], the circuit outputs the four Bell states (listed above). More generally, the circuit transforms the input in accordance with the equation

[math]\displaystyle{ |\beta(x,y)\rangle = \left ( \frac{|0,y\rangle + (-1)^x|1,\bar{y}\rangle}{\sqrt{2}} \right ), }[/math]

where [math]\displaystyle{ \bar{y} }[/math] is the negation of [math]\displaystyle{ y }[/math].

Properties of Bell states

The result of a measurement of a single qubit in a Bell state is indeterminate, but upon measuring the first qubit in the z-basis, the result of measuring the second qubit is guaranteed to yield the same value (for the [math]\displaystyle{ \Phi }[/math] Bell states) or the opposite value (for the [math]\displaystyle{ \Psi }[/math] Bell states). This implies that the measurement outcomes are correlated. John Bell was the first to prove that the measurement correlations in the Bell State are stronger than could ever exist between classical systems. This hints that quantum mechanics allows information processing beyond what is possible with classical mechanics. In addition, the Bell states form an orthonormal basis and can therefore be defined with an appropriate measurement. Because Bell states are entangled states, information on the entire system may be known, while withholding information on the individual subsystems. For example, the Bell state is a pure state, but the reduced density operator of the first qubit is a mixed state. The mixed state implies that not all the information on this first qubit is known. Bell States are either symmetric or antisymmetric with respect to the subsystems. Bell states are maximally entangled in the sense that its reduced density operators are maximally mixed, the multipartite generalization of Bell states in this spirit is called the absolutely maximally entangled (AME) state.

Bell state measurement

The Bell measurement is an important concept in quantum information science: It is a joint quantum-mechanical measurement of two qubits that determines which of the four Bell states the two qubits are in.

Quantum circuit that performs Bell decoding. Bell states are sometimes called EPR pairs. Notice that the circuit that decodes the Bell state is the adjoint to the circuit that encodes, or creates, Bell states (described above).

A helpful example of quantum measurement in the Bell basis can be seen in quantum computing. If a CNOT gate is applied to qubits A and B, followed by a Hadamard gate on qubit A, a measurement can be made in the computational basis. The CNOT gate performs the act of un-entangling the two previously entangled qubits. This allows the information to be converted from quantum information to a measurement of classical information.

Quantum measurement obeys two key principles. The first, the principle of deferred measurement, states that any measurement can be moved to the end of the circuit. The second principle, the principle of implicit measurement, states that at the end of a quantum circuit, measurement can be assumed for any unterminated wires.

The following are applications of Bell state measurements:

Bell state measurement is the crucial step in quantum teleportation. The result of a Bell state measurement is used by one's co-conspirator to reconstruct the original state of a teleported particle from half of an entangled pair (the "quantum channel") that was previously shared between the two ends.

Experiments that utilize so-called "linear evolution, local measurement" techniques cannot realize a complete Bell state measurement. Linear evolution means that the detection apparatus acts on each particle independent of the state or evolution of the other, and local measurement means that each particle is localized at a particular detector registering a "click" to indicate that a particle has been detected. Such devices can be constructed from, for example: mirrors, beam splitters, and wave plates – and are attractive from an experimental perspective because they are easy to use and have a high measurement cross-section.

For entanglement in a single qubit variable, only three distinct classes out of four Bell states are distinguishable using such linear optical techniques. This means two Bell states cannot be distinguished from each other, limiting the efficiency of quantum communication protocols such as teleportation. If a Bell state is measured from this ambiguous class, the teleportation event fails.

Entangling particles in multiple qubit variables, such as (for photonic systems) polarization and a two-element subset of orbital angular momentum states, allows the experimenter to trace over one variable and achieve a complete Bell state measurement in the other. Leveraging so-called hyper-entangled systems thus has an advantage for teleportation. It also has advantages for other protocols such as superdense coding, in which hyper-entanglement increases the channel capacity.

In general, for hyper-entanglement in [math]\displaystyle{ n }[/math] variables, one can distinguish between at most [math]\displaystyle{ 2^{n+1} - 1 }[/math] classes out of [math]\displaystyle{ 4^n }[/math] Bell states using linear optical techniques.

Bell state correlations

Independent measurements made on two qubits that are entangled in Bell states positively correlate perfectly if each qubit is measured in the relevant basis. For the [math]\displaystyle{ |\Phi^+\rangle }[/math] state, this means selecting the same basis for both qubits. If an experimenter chose to measure both qubits in a [math]\displaystyle{ |\Phi^-\rangle }[/math] Bell state using the same basis, the qubits would appear positively correlated when measuring in the [math]\displaystyle{ \{|0\rangle,|1\rangle\} }[/math] basis, anti-correlated in the [math]\displaystyle{ \{|+\rangle,|-\rangle\} }[/math] basis, and partially (probabilistically) correlated in other bases.

The [math]\displaystyle{ |\Psi^+\rangle }[/math] correlations can be understood by measuring both qubits in the same basis and observing perfectly anti-correlated results. More generally, [math]\displaystyle{ |\Psi^+\rangle }[/math] can be understood by measuring the first qubit in basis [math]\displaystyle{ b_1 }[/math], the second qubit in basis [math]\displaystyle{ b_2 = X.b_1 }[/math], and observing perfectly positively correlated results.

Relationship between the correlated bases of two qubits in the [math]\displaystyle{ |\Phi^-\rangle }[/math] state.

Bell state	Basis [math]\displaystyle{ b_2 }[/math]
[math]\displaystyle{ |\Phi^+\rangle }[/math]	[math]\displaystyle{ b_1 }[/math]
[math]\displaystyle{ |\Phi^-\rangle }[/math]	[math]\displaystyle{ Z.b_1 }[/math]
[math]\displaystyle{ |\Psi^+\rangle }[/math]	[math]\displaystyle{ X.b_1 }[/math]
[math]\displaystyle{ |\Psi^-\rangle }[/math]	[math]\displaystyle{ X.Z.b_1 }[/math]

Applications

Superdense coding

Superdense coding allows two individuals to communicate two bits of classical information by only sending a single qubit. The basis of this phenomenon is the entangled states or Bell states of a two qubit system. In this example, Alice and Bob are very far from each other, and have each been given one qubit of the entangled state.

[math]\displaystyle{ |\psi \rangle = \frac{|00\rangle + |11\rangle}{\sqrt{2}} }[/math].

In this example, Alice is trying to communicate two bits of classical information, one of four two bit strings: [math]\displaystyle{ '00', '01', '10', }[/math]or [math]\displaystyle{ '11' }[/math]. If Alice chooses to send the two bit message [math]\displaystyle{ '01' }[/math], she would perform the phase flip [math]\displaystyle{ Z }[/math] to her qubit. Similarly, if Alice wants to send [math]\displaystyle{ '10' }[/math], she would apply a NOT gate; if she wanted to send [math]\displaystyle{ '11' }[/math], she would apply the [math]\displaystyle{ iY }[/math]gate to her qubit; and finally, if Alice wanted to send the two bit message [math]\displaystyle{ '00' }[/math], she would do nothing to her qubit. Alice performs these quantum gate transformations locally, transforming the initial entangled state [math]\displaystyle{ |\psi\rangle }[/math] into one of the four Bell states.

The steps below show the necessary quantum gate transformations, and resulting Bell states, that Alice needs to apply to her qubit for each possible two bit message she desires to send to Bob.

[math]\displaystyle{ 00: I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \longrightarrow |\psi \rangle = \frac{|00\rangle + |11\rangle}{\sqrt2}\equiv |{\Phi^+}\rangle }[/math]

[math]\displaystyle{ 01: Z = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}\longrightarrow |\psi \rangle = \frac{|00\rangle - |11\rangle}{\sqrt2}\equiv |{\Phi^-}\rangle }[/math]

[math]\displaystyle{ 10: X = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\longrightarrow |\psi \rangle = \frac{|01\rangle + |10\rangle}{\sqrt2}\equiv |{\Psi^+}\rangle }[/math]

[math]\displaystyle{ 11: -iY = XZ = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}\longrightarrow |\psi \rangle = \frac{|01\rangle - |10\rangle}{\sqrt2}\equiv |{\Psi^-}\rangle }[/math].

After Alice applies the desired transformations to her qubit, she sends it to Bob. Bob then performs a measurement on the Bell state, which projects the entangled state onto one of the four two-qubit basis vectors, one of which will coincide with the original two bit message Alice was trying to send.

Quantum teleportation

Quantum teleportation is the transfer of a quantum state over a distance. It is facilitated by entanglement between A, the giver, and B, the receiver of this quantum state. This process has become a fundamental research topic for quantum communication and computing. More recently, scientists have been testing its applications in information transfer through optical fibers. The process of quantum teleportation is defined as the following:

Alice and Bob share an EPR pair and each took one qubit before they became separated. Alice must deliver a qubit of information to Bob, but she does not know the state of this qubit and can only send classical information to Bob.

It is performed step by step as the following:

1. Alice sends her qubits through a CNOT gate.
2. Alice then sends the first qubit through a Hadamard gate.
3. Alice measures her qubits, obtaining one of four results, and sends this information to Bob.
4. Given Alice's measurements, Bob performs one of four operations on his half of the EPR pair and recovers the original quantum state.

The following quantum circuit describes teleportation:

Quantum circuit for teleporting a qubit

Quantum cryptography

Quantum cryptography is the use of quantum mechanical properties in order to encode and send information safely. The theory behind this process is the fact that it is impossible to measure a quantum state of a system without disturbing the system. This can be used to detect eavesdropping within a system.

The most common form of quantum cryptography is quantum key distribution. It enables two parties to produce a shared random secret key that can be used to encrypt messages. Its private key is created between the two parties through a public channel.

Quantum cryptography can be considered a state of entanglement between two multi-dimensional systems, also known as two-qudit (quantum digit) entanglement.

See also

• Bell test experiments
• Bell's inequality
• EPR paradox
• GHZ state
• Superdense coding
• Quantum teleportation
• Quantum cryptography
• Quantum circuits
• Bell diagonal state

References

• Nielsen, Michael A.; Chuang, Isaac L. (2000), Quantum computation and quantum information, Cambridge University Press, ISBN 978-0-521-63503-5 , pp. 25.
• Kaye, Phillip; Laflamme, Raymond; Mosca, Michele (2007), An introduction to quantum computing, Oxford University Press, ISBN 978-0-19-857049-3 , pp. 75.
• On the Einstein Podolsky and Rosen paradox, Bell System Technical Journal, 1964 .