Quantum logic gate
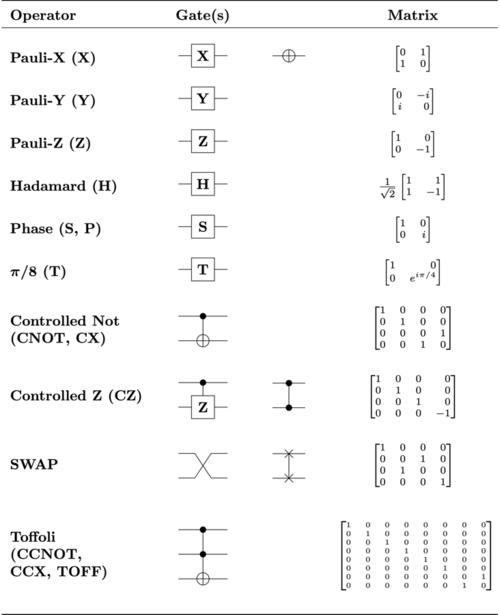
In quantum computing and specifically the quantum circuit model of computation, a quantum logic gate (or simply quantum gate) is a basic quantum circuit operating on a small number of qubits. Quantum logic gates are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.
Unlike many classical logic gates, quantum logic gates are reversible. It is possible to perform classical computing using only reversible gates. For example, the reversible Toffoli gate can implement all Boolean functions, often at the cost of having to use ancilla bits. The Toffoli gate has a direct quantum equivalent, showing that quantum circuits can perform all operations performed by classical circuits.
Quantum gates are unitary operators, and are described as unitary matrices relative to some orthonormal basis. Usually the computational basis is used, which unless comparing it with something, just means that for a d-level quantum system (such as a qubit, a quantum register, or qutrits and qudits)[1]: 22–23 the orthonormal basis vectors are labeled , or use binary notation.
History
The current notation for quantum gates was developed by many of the founders of quantum information science including Adriano Barenco, Charles Bennett, Richard Cleve, David P. DiVincenzo, Norman Margolus, Peter Shor, Tycho Sleator, John A. Smolin, and Harald Weinfurter,[2] building on notation introduced by Richard Feynman in 1986.[3]
Representation

Rotations about the x, y, z axes of the Bloch sphere are represented by the rotation operator gates.
Quantum logic gates are represented by unitary matrices. A gate that acts on qubits (a register) is represented by a unitary matrix, and the set of all such gates with the group operation of matrix multiplication[lower-alpha 1] is the unitary group U(2n).[2] The quantum states that the gates act upon are unit vectors in complex dimensions, with the complex Euclidean norm (the 2-norm).[4]: 66 [5]: 56, 65 The basis vectors (sometimes called eigenstates) are the possible outcomes if the state of the qubits is measured, and a quantum state is a linear combination of these outcomes. The most common quantum gates operate on vector spaces of one or two qubits, just like the common classical logic gates operate on one or two bits.
Even though the quantum logic gates belong to continuous symmetry groups, real hardware is inexact and thus limited in precision. The application of gates typically introduces errors, and the quantum states' fidelities decrease over time. If error correction is used, the usable gates are further restricted to a finite set.[4]: ch. 10 [1]: ch. 14 Later in this article, this is ignored as the focus is on the ideal quantum gates' properties.
Quantum states are typically represented by "kets", from a notation known as bra–ket.
The vector representation of a single qubit is
Here, and are the complex probability amplitudes of the qubit. These values determine the probability of measuring a 0 or a 1, when measuring the state of the qubit. See measurement below for details.
The value zero is represented by the ket , and the value one is represented by the ket .
The tensor product (or Kronecker product) is used to combine quantum states. The combined state for a qubit register is the tensor product of the constituent qubits. The tensor product is denoted by the symbol .
The vector representation of two qubits is:[6]
The action of the gate on a specific quantum state is found by multiplying the vector , which represents the state by the matrix representing the gate. The result is a new quantum state :
Relation to the time evolution operator
The Schrödinger equation describes how quantum systems that are not observed evolve over time, and is When the system is in a stable environment, so it has a constant Hamiltonian, the solution to this equation is [1]: 24–25 If the time is always the same it may be omitted for simplicity, and the way quantum states evolve can be described as just as in the above section.
That is, a quantum gate is how a quantum system that is not observed evolves over some specific time, or equivalently, a gate is the unitary time evolution operator acting on a quantum state for a specific duration.
Notable examples
There exists an uncountably infinite number of gates. Some of them have been named by various authors,[1][2][4][5][7][8][9] and below follow some of those most often used in the literature.
Identity gate
The identity gate is the identity matrix, usually written as I, and is defined for a single qubit as
where I is basis independent and does not modify the quantum state. The identity gate is most useful when describing mathematically the result of various gate operations or when discussing multi-qubit circuits.
Pauli gates (X,Y,Z)
The Pauli gates are the three Pauli matrices and act on a single qubit. The Pauli X, Y and Z equate, respectively, to a rotation around the x, y and z axes of the Bloch sphere by radians.[lower-alpha 2]
The Pauli-X gate is the quantum equivalent of the NOT gate for classical computers with respect to the standard basis , , which distinguishes the z axis on the Bloch sphere. It is sometimes called a bit-flip as it maps to and to . Similarly, the Pauli-Y maps to and to . Pauli Z leaves the basis state unchanged and maps to . Due to this nature, Pauli Z is sometimes called phase-flip.
These matrices are usually represented as
The Pauli matrices are involutory, meaning that the square of a Pauli matrix is the identity matrix.
The Pauli matrices also anti-commute, for example
The matrix exponential of a Pauli matrix is a rotation operator, often written as
Controlled gates

Controlled gates act on 2 or more qubits, where one or more qubits act as a control for some operation.[2] For example, the controlled NOT gate (or CNOT or CX) acts on 2 qubits, and performs the NOT operation on the second qubit only when the first qubit is , and otherwise leaves it unchanged. With respect to the basis , , , , it is represented by the Hermitian unitary matrix:
The CNOT (or controlled Pauli-X) gate can be described as the gate that maps the basis states , where is XOR.
The CNOT can be expressed in the Pauli basis as:
Being a Hermitian unitary operator, CNOT has the property that and , and is involutory.
More generally if U is a gate that operates on a single qubit with matrix representation
then the controlled-U gate is a gate that operates on two qubits in such a way that the first qubit serves as a control. It maps the basis states as follows.
The matrix representing the controlled U is
When U is one of the Pauli operators, X,Y, Z, the respective terms "controlled-X", "controlled-Y", or "controlled-Z" are sometimes used.[4]: 177–185 Sometimes this is shortened to just CX, CY and CZ.
In general, any single qubit unitary gate can be expressed as , where H is a Hermitian matrix, and then the controlled U is
Control can be extended to gates with arbitrary number of qubits[2] and functions in programming languages.[10] Functions can be conditioned on superposition states.[11][12]
Classical control

In circuit diagrams, single lines are qubits, and doubled lines are bits.
Gates can also be controlled by classical logic. A quantum computer is controlled by a classical computer, and behaves like a coprocessor that receives instructions from the classical computer about what gates to execute on which qubits.[13]: 42–43 [14] Classical control is simply the inclusion, or omission, of gates in the instruction sequence for the quantum computer.[4]: 26–28 [1]: 87–88
Phase shift gates
The phase shift is a family of single-qubit gates that map the basis states and . The probability of measuring a or is unchanged after applying this gate, however it modifies the phase of the quantum state. This is equivalent to tracing a horizontal circle (a line of constant latitude), or a rotation about the z-axis on the Bloch sphere by radians. The phase shift gate is represented by the matrix:
where is the phase shift with the period 2π. Some common examples are the T gate where (historically known as the gate), the phase gate (also known as the S gate, written as S, though S is sometimes used for SWAP gates) where and the Pauli-Z gate where
The phase shift gates are related to each other as follows:
Note that the phase gate is not Hermitian (except for all ). These gates are different from their Hermitian conjugates: . The two adjoint (or conjugate transpose) gates and are sometimes included in instruction sets.[15][16]
Hadamard gate
The Hadamard or Walsh-Hadamard gate, named after Jacques Hadamard (fr) and Joseph L. Walsh, acts on a single qubit. It maps the basis states
and
(it creates an equal superposition state if given a computational basis state). The two states
and
are sometimes written
and
respectively. The Hadamard gate performs a rotation of
about the axis
at the Bloch sphere, and is therefore involutory. It is represented by the Hadamard matrix:

If the Hermitian (so ) Hadamard gate is used to perform a change of basis, it flips and . For example, and
Swap gate

The swap gate swaps two qubits. With respect to the basis , , , , it is represented by the matrix
The swap gate can be decomposed into summation form:
Toffoli (CCNOT) gate

The Toffoli gate, named after Tommaso Toffoli and also called the CCNOT gate or Deutsch gate , is a 3-bit gate that is universal for classical computation but not for quantum computation. The quantum Toffoli gate is the same gate, defined for 3 qubits. If we limit ourselves to only accepting input qubits that are and , then if the first two bits are in the state it applies a Pauli-X (or NOT) on the third bit, else it does nothing. It is an example of a CC-U (controlled-controlled Unitary) gate. Since it is the quantum analog of a classical gate, it is completely specified by its truth table. The Toffoli gate is universal when combined with the single qubit Hadamard gate.[17]
| Truth table | Matrix form | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
The Toffoli gate is related to the classical AND () and XOR () operations as it performs the mapping on states in the computational basis.
The Toffoli gate can be expressed using Pauli matrices as
Universal quantum gates

A set of universal quantum gates is any set of gates to which any operation possible on a quantum computer can be reduced, that is, any other unitary operation can be expressed as a finite sequence of gates from the set. Technically, this is impossible with anything less than an uncountable set of gates since the number of possible quantum gates is uncountable, whereas the number of finite sequences from a finite set is countable. To solve this problem, we only require that any quantum operation can be approximated by a sequence of gates from this finite set. Moreover, for unitaries on a constant number of qubits, the Solovay–Kitaev theorem guarantees that this can be done efficiently. Checking if a set of quantum gates is universal can be done using group theory methods[18] and/or relation to (approximate) unitary t-designs[19]
Some universal quantum gate sets include:
- The rotation operators Rx(θ), Ry(θ), Rz(θ), the phase shift gate P(φ)[lower-alpha 3] and CNOT are commonly used to form a universal quantum gate set.[20][lower-alpha 4]
- The Clifford set {CNOT, H, S} + T gate. The Clifford set alone is not a universal quantum gate set, as it can be efficiently simulated classically according to the Gottesman–Knill theorem.
- The Toffoli gate + Hadamard gate.[17] The Toffoli gate alone forms a set of universal gates for reversible Boolean algebraic logic circuits, which encompasses all classical computation.
Deutsch gate
A single-gate set of universal quantum gates can also be formulated using the parametrized three-qubit Deutsch gate ,[21] named after physicist David Deutsch. It is a general case of CC-U, or controlled-controlled-unitary gate, and is defined as
Unfortunately, a working Deutsch gate has remained out of reach, due to lack of a protocol. There are some proposals to realize a Deutsch gate with dipole–dipole interaction in neutral atoms.[22]
A universal logic gate for reversible classical computing, the Toffoli gate, is reducible to the Deutsch gate , thus showing that all reversible classical logic operations can be performed on a universal quantum computer.
There also exist single two-qubit gates sufficient for universality. In 1996, Adriano Barenco showed that the Deutsch gate can be decomposed using only a single two-qubit gate (Barenco gate), but it is hard to realize experimentally.[1]: 93 This feature is exclusive to quantum circuits, as there is no classical two-bit gate that is both reversible and universal.[1]: 93 Universal two-qubit gates could be implemented to improve classical reversible circuits in fast low-power microprocessors.[1]: 93
Circuit composition
Serially wired gates

Assume that we have two gates A and B that both act on
qubits. When B is put after A in a series circuit, then the effect of the two gates can be described as a single gate C.
where is matrix multiplication. The resulting gate C will have the same dimensions as A and B. The order in which the gates would appear in a circuit diagram is reversed when multiplying them together.[4]: 17–18,22–23,62–64 [5]: 147–169
For example, putting the Pauli X gate after the Pauli Y gate, both of which act on a single qubit, can be described as a single combined gate C:
The product symbol () is often omitted.
Exponents of quantum gates
All real exponents of unitary matrices are also unitary matrices, and all quantum gates are unitary matrices.
Positive integer exponents are equivalent to sequences of serially wired gates (e.g. ), and the real exponents is a generalization of the series circuit. For example, and are both valid quantum gates.
for any unitary matrix . The identity matrix () behaves like a NOP[23][24] and can be represented as bare wire in quantum circuits, or not shown at all.
All gates are unitary matrices, so that and , where is the conjugate transpose. This means that negative exponents of gates are unitary inverses of their positively exponentiated counterparts: . For example, some negative exponents of the phase shift gates are and .
Note that for a Hermitian matrix and because of unitarity, so for all Hermitian gates. They are involutory. Examples of Hermitian gates are the Pauli gates, Hadamard, CNOT, SWAP and Toffoli. Each Hermitian unitary matrix has the property that where
The exponent of a gate is a multiple of the duration of time that the time evolution operator is applied to a quantum state. E.g., in a spin qubit quantum computer the gate could be realized via exchange interaction on the spin of two electrons for half the duration of a full exchange interaction.[25]
Parallel gates

The tensor product (or Kronecker product) of two quantum gates is the gate that is equal to the two gates in parallel.[4]: 71–75 [5]: 148
If we, as in the picture, combine the Pauli-Y gate with the Pauli-X gate in parallel, then this can be written as:
Both the Pauli-X and the Pauli-Y gate act on a single qubit. The resulting gate act on two qubits.
Sometimes the tensor product symbol is omitted, and indexes are used for the operators instead.[25]
Hadamard transform
The gate is the Hadamard gate () applied in parallel on 2 qubits. It can be written as:
This "two-qubit parallel Hadamard gate" will, when applied to, for example, the two-qubit zero-vector (), create a quantum state that has equal probability of being observed in any of its four possible outcomes; , , , and . We can write this operation as:

Here the amplitude for each measurable state is 1⁄2. The probability to observe any state is the square of the absolute value of the measurable states amplitude, which in the above example means that there is one in four that we observe any one of the individual four cases. See measurement for details.
performs the Hadamard transform on two qubits. Similarly the gate performs a Hadamard transform on a register of qubits.
When applied to a register of qubits all initialized to , the Hadamard transform puts the quantum register into a superposition with equal probability of being measured in any of its possible states:
This state is a uniform superposition and it is generated as the first step in some search algorithms, for example in amplitude amplification and phase estimation.
Measuring this state results in a random number between and .[lower-alpha 5] How random the number is depends on the fidelity of the logic gates. If not measured, it is a quantum state with equal probability amplitude for each of its possible states.
The Hadamard transform acts on a register with qubits such that as follows:
Application on entangled states
If two or more qubits are viewed as a single quantum state, this combined state is equal to the tensor product of the constituent qubits. Any state that can be written as a tensor product from the constituent subsystems are called separable states. On the other hand, an entangled state is any state that cannot be tensor-factorized, or in other words: An entangled state can not be written as a tensor product of its constituent qubits states. Special care must be taken when applying gates to constituent qubits that make up entangled states.
If we have a set of N qubits that are entangled and wish to apply a quantum gate on M < N qubits in the set, we will have to extend the gate to take N qubits. This application can be done by combining the gate with an identity matrix such that their tensor product becomes a gate that act on N qubits. The identity matrix () is a representation of the gate that maps every state to itself (i.e., does nothing at all). In a circuit diagram the identity gate or matrix will often appear as just a bare wire.

For example, the Hadamard gate () acts on a single qubit, but if we feed it the first of the two qubits that constitute the entangled Bell state , we cannot write that operation easily. We need to extend the Hadamard gate with the identity gate so that we can act on quantum states that span two qubits:
The gate can now be applied to any two-qubit state, entangled or otherwise. The gate will leave the second qubit untouched and apply the Hadamard transform to the first qubit. If applied to the Bell state in our example, we may write that as:
Computational complexity and the tensor product
The time complexity for multiplying two -matrices is at least ,[26] if using a classical machine. Because the size of a gate that operates on qubits is it means that the time for simulating a step in a quantum circuit (by means of multiplying the gates) that operates on generic entangled states is . For this reason it is believed to be intractable to simulate large entangled quantum systems using classical computers. Subsets of the gates, such as the Clifford gates, or the trivial case of circuits that only implement classical Boolean functions (e.g. combinations of X, CNOT, Toffoli), can however be efficiently simulated on classical computers.
The state vector of a quantum register with qubits is complex entries. Storing the probability amplitudes as a list of floating point values is not tractable for large .
Unitary inversion of gates

Because all quantum logical gates are reversible, any composition of multiple gates is also reversible. All products and tensor products (i.e. series and parallel combinations) of unitary matrices are also unitary matrices. This means that it is possible to construct an inverse of all algorithms and functions, as long as they contain only gates.
Initialization, measurement, I/O and spontaneous decoherence are side effects in quantum computers. Gates however are purely functional and bijective.
If is a unitary matrix, then and . The dagger () denotes the conjugate transpose. It is also called the Hermitian adjoint.
If a function is a product of gates, , the unitary inverse of the function can be constructed:
Because we have, after repeated application on itself
Similarly if the function consists of two gates and in parallel, then and .
Gates that are their own unitary inverses are called Hermitian or self-adjoint operators. Some elementary gates such as the Hadamard (H) and the Pauli gates (I, X, Y, Z) are Hermitian operators, while others like the phase shift (S, T, P, CPhase) gates generally are not.
For example, an algorithm for addition can be used for subtraction, if it is being "run in reverse", as its unitary inverse. The inverse quantum Fourier transform is the unitary inverse. Unitary inverses can also be used for uncomputation. Programming languages for quantum computers, such as Microsoft's Q#,[10] Bernhard Ömer's QCL,[13]: 61 and IBM's Qiskit,[27] contain function inversion as programming concepts.
Measurement

Measurement (sometimes called observation) is irreversible and therefore not a quantum gate, because it assigns the observed quantum state to a single value. Measurement takes a quantum state and projects it to one of the basis vectors, with a likelihood equal to the square of the vector's length (in the 2-norm[4]: 66 [5]: 56, 65 ) along that basis vector.[1]: 15–17 [28][29][30] This is known as the Born rule and appears[lower-alpha 5] as a stochastic non-reversible operation as it probabilistically sets the quantum state equal to the basis vector that represents the measured state. At the instant of measurement, the state is said to "collapse" to the definite single value that was measured. Why and how, or even if[31][32] the quantum state collapses at measurement, is called the measurement problem.
The probability of measuring a value with probability amplitude is , where is the modulus.
Measuring a single qubit, whose quantum state is represented by the vector , will result in with probability , and in with probability .
For example, measuring a qubit with the quantum state will yield with equal probability either or .

Note: is the probability of measuring and is the probability of measuring .
A quantum state that spans n qubits can be written as a vector in complex dimensions: . This is because the tensor product of n qubits is a vector in dimensions. This way, a register of n qubits can be measured to distinct states, similar to how a register of n classical bits can hold distinct states. Unlike with the bits of classical computers, quantum states can have non-zero probability amplitudes in multiple measurable values simultaneously. This is called superposition.
The sum of all probabilities for all outcomes must always be equal to 1.[lower-alpha 6] Another way to say this is that the Pythagorean theorem generalized to has that all quantum states with n qubits must satisfy [lower-alpha 7] where is the probability amplitude for measurable state . A geometric interpretation of this is that the possible value-space of a quantum state with n qubits is the surface of the unit sphere in and that the unitary transforms (i.e. quantum logic gates) applied to it are rotations on the sphere. The rotations that the gates perform form the symmetry group U(2n). Measurement is then a probabilistic projection of the points at the surface of this complex sphere onto the basis vectors that span the space (and labels the outcomes).
In many cases the space is represented as a Hilbert space rather than some specific -dimensional complex space. The number of dimensions (defined by the basis vectors, and thus also the possible outcomes from measurement) is then often implied by the operands, for example as the required state space for solving a problem. In Grover's algorithm, Grover named this generic basis vector set "the database".
The selection of basis vectors against which to measure a quantum state will influence the outcome of the measurement.[1]: 30–35 [4]: 22, 84–85, 185–188 [33] See change of basis and Von Neumann entropy for details. In this article, we always use the computational basis, which means that we have labeled the basis vectors of an n-qubit register , or use the binary representation .
In quantum mechanics, the basis vectors constitute an orthonormal basis.
An example of usage of an alternative measurement basis is in the BB84 cipher.
The effect of measurement on entangled states
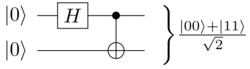
If two quantum states (i.e. qubits, or registers) are entangled (meaning that their combined state cannot be expressed as a tensor product), measurement of one register affects or reveals the state of the other register by partially or entirely collapsing its state too. This effect can be used for computation, and is used in many algorithms.
The Hadamard-CNOT combination acts on the zero-state as follows:

This resulting state is the Bell state . It cannot be described as a tensor product of two qubits. There is no solution for
because for example w needs to be both non-zero and zero in the case of xw and yw.
The quantum state spans the two qubits. This is called entanglement. Measuring one of the two qubits that make up this Bell state will result in that the other qubit logically must have the same value, both must be the same: Either it will be found in the state , or in the state . If we measure one of the qubits to be for example , then the other qubit must also be , because their combined state became . Measurement of one of the qubits collapses the entire quantum state, that span the two qubits.
The GHZ state is a similar entangled quantum state that spans three or more qubits.
This type of value-assignment occurs instantaneously over any distance and this has as of 2018 been experimentally verified by QUESS for distances of up to 1200 kilometers.[34][35][36] That the phenomena appears to happen instantaneously as opposed to the time it would take to traverse the distance separating the qubits at the speed of light is called the EPR paradox, and it is an open question in physics how to resolve this. Originally it was solved by giving up the assumption of local realism, but other interpretations have also emerged. For more information see the Bell test experiments. The no-communication theorem proves that this phenomenon cannot be used for faster-than-light communication of classical information.
Measurement on registers with pairwise entangled qubits
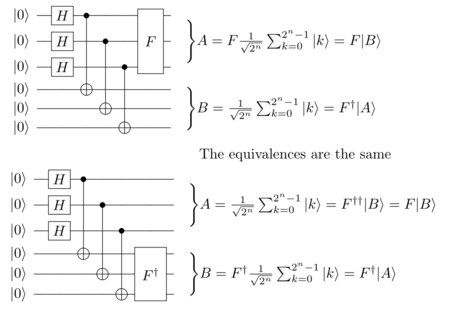
Take a register A with n qubits all initialized to , and feed it through a parallel Hadamard gate . Register A will then enter the state that have equal probability of when measured to be in any of its possible states; to . Take a second register B, also with n qubits initialized to and pairwise CNOT its qubits with the qubits in register A, such that for each p the qubits and forms the state .
If we now measure the qubits in register A, then register B will be found to contain the same value as A. If we however instead apply a quantum logic gate F on A and then measure, then , where is the unitary inverse of F.
Because of how unitary inverses of gates act, . For example, say , then .
The equality will hold no matter in which order measurement is performed (on the registers A or B), assuming that F has run to completion. Measurement can even be randomly and concurrently interleaved qubit by qubit, since the measurements assignment of one qubit will limit the possible value-space from the other entangled qubits.
Even though the equalities holds, the probabilities for measuring the possible outcomes may change as a result of applying F, as may be the intent in a quantum search algorithm.
This effect of value-sharing via entanglement is used in Shor's algorithm, phase estimation and in quantum counting. Using the Fourier transform to amplify the probability amplitudes of the solution states for some problem is a generic method known as "Fourier fishing".[37]
Logic function synthesis

Functions and routines that only use gates can themselves be described as matrices, just like the smaller gates. The matrix that represents a quantum function acting on qubits has size . For example, a function that acts on a "qubyte" (a register of 8 qubits) would be represented by a matrix with elements.
Unitary transformations that are not in the set of gates natively available at the quantum computer (the primitive gates) can be synthesised, or approximated, by combining the available primitive gates in a circuit. One way to do this is to factor the matrix that encodes the unitary transformation into a product of tensor products (i.e. series and parallel circuits) of the available primitive gates. The group U(2q) is the symmetry group for the gates that act on qubits.[2] Factorization is then the problem of finding a path in U(2q) from the generating set of primitive gates. The Solovay–Kitaev theorem shows that given a sufficient set of primitive gates, there exist an efficient approximate for any gate. For the general case with a large number of qubits this direct approach to circuit synthesis is intractable.[38][39] This puts a limit on how large functions can be brute-force factorized into primitive quantum gates. Typically quantum programs are instead built using relatively small and simple quantum functions, similar to normal classical programming.
Because of the gates unitary nature, all functions must be reversible and always be bijective mappings of input to output. There must always exist a function such that . Functions that are not invertible can be made invertible by adding ancilla qubits to the input or the output, or both. After the function has run to completion, the ancilla qubits can then either be uncomputed or left untouched. Measuring or otherwise collapsing the quantum state of an ancilla qubit (e.g. by re-initializing the value of it, or by its spontaneous decoherence) that have not been uncomputed may result in errors,[40][41] as their state may be entangled with the qubits that are still being used in computations.
Logically irreversible operations, for example addition modulo of two -qubit registers a and b, ,[lower-alpha 8] can be made logically reversible by adding information to the output, so that the input can be computed from the output (i.e. there exists a function ). In our example, this can be done by passing on one of the input registers to the output: . The output can then be used to compute the input (i.e. given the output and , we can easily find the input; is given and ) and the function is made bijective.
All Boolean algebraic expressions can be encoded as unitary transforms (quantum logic gates), for example by using combinations of the Pauli-X, CNOT and Toffoli gates. These gates are functionally complete in the Boolean logic domain.
There are many unitary transforms available in the libraries of Q#, QCL, Qiskit, and other quantum programming languages. It also appears in the literature.[42][43]
For example, , where is the number of qubits that constitutes the register , is implemented as the following in QCL:[44][13][12]
cond qufunct inc(qureg x) { // increment register
int i;
for i = #x-1 to 0 step -1 {
CNot(x[i], x[0::i]); // apply controlled-not from
} // MSB to LSB
}

In QCL, decrement is done by "undoing" increment. The prefix ! is used to instead run the unitary inverse of the function. !inc(x) is the inverse of inc(x) and instead performs the operation . The cond keyword means that the function can be conditional.[11]
In the model of computation used in this article (the quantum circuit model), a classic computer generates the gate composition for the quantum computer, and the quantum computer behaves as a coprocessor that receives instructions from the classical computer about which primitive gates to apply to which qubits.[13]: 36–43 [14] Measurement of quantum registers results in binary values that the classical computer can use in its computations. Quantum algorithms often contain both a classical and a quantum part. Unmeasured I/O (sending qubits to remote computers without collapsing their quantum states) can be used to create networks of quantum computers. Entanglement swapping can then be used to realize distributed algorithms with quantum computers that are not directly connected. Examples of distributed algorithms that only require the use of a handful of quantum logic gates are superdense coding, the quantum Byzantine agreement and the BB84 cipherkey exchange protocol.
See also
- Adiabatic quantum computation
- BQP
- Cellular automaton
- Cloud-based quantum computing
- Counterfactual definiteness
- Counterfactual quantum computation
- Landauer's principle
- Logical connective
- One-way quantum computer
- Quantum algorithm
- Quantum cellular automaton
- Quantum channel
- Quantum finite automaton
- Quantum logic
- Quantum memory
- Quantum network
- Quantum Zeno effect
- Reversible computing
- Unitary transformation (quantum mechanics)
Notes
- ↑ Matrix multiplication of quantum gates is defined as series circuits.
- ↑ Note, here a full rotation about the Bloch sphere is radians, as opposed to the rotation operator gates where a full turn is
- ↑ Either the P or Ph gate can be used, as [2]: 11 [1]: 76–83
- ↑ This set generates every possible unitary gate exactly. However as the global phase is irrelevant in the measurement output, universal quantum subsets can be constructed e.g. the set containing Ry(θ),Rz(θ) and CNOT only spans all unitaries with determinant ±1 but it is sufficient for quantum computation.
- ↑ 5.0 5.1 If this actually is a stochastic effect depends on which interpretation of quantum mechanics that is correct (and if any interpretation can be correct). For example, De Broglie–Bohm theory and the many-worlds interpretation asserts determinism. (In the many-worlds interpretation, a quantum computer is a machine that runs programs (quantum circuits) that selects a reality where the probability of it having the solution states of a problem is large. That is, the machine more often than not ends up in a reality where it gives the correct answer. Because all outcomes are realized in separate universes according to the many-worlds interpretation, the total outcome is deterministic. This interpretation does however not change the mechanics by which the machine operates.)
- ↑ See Probability axioms § Second axiom
- ↑ The hypotenuse has length 1 because the probabilities sum to 1, so the quantum state vector is a unit vector.
- ↑ The input is qubits, but the output is just qubits. Information erasure is not a reversible (or unitary) operation, and therefore not allowed. See also Landauer's principle.
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Williams, Colin P. (2011). Explorations in Quantum Computing. Springer. ISBN 978-1-84628-887-6.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 Barenco, Adriano; Bennett, Charles H.; Cleve, Richard; DiVincenzo, David P.; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A. et al. (1995-11-01). "Elementary gates for quantum computation". Physical Review A (American Physical Society (APS)) 52 (5): 3457–3467. doi:10.1103/physreva.52.3457. ISSN 1050-2947. PMID 9912645. Bibcode: 1995PhRvA..52.3457B.
- ↑ 3.0 3.1 Feynman, Richard P. (1986). "Quantum mechanical computers". Foundations of Physics (Springer Science and Business Media LLC) 16 (6): 507–531. doi:10.1007/bf01886518. ISSN 0015-9018. Bibcode: 1986FoPh...16..507F.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 Nielsen, Michael A.; Chuang, Isaac (2010). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 978-1-10700-217-3. OCLC 43641333. https://www.cambridge.org/9781107002173.
- ↑ 5.0 5.1 5.2 5.3 5.4 Yanofsky, Noson S.; Mannucci, Mirco (2013). Quantum computing for computer scientists. Cambridge University Press. ISBN 978-0-521-87996-5.
- ↑ Preskill, John (2021-06-06). "Quantum computing 40 years later". pp. 10–15. arXiv:2106.10522 [quant-ph].
- ↑ "Circuit Library". IBM (Qiskit). https://qiskit.org/documentation/apidoc/circuit_library.html.
- ↑ "cQASM: Qubit gate operations". QuTech. https://www.quantum-inspire.com/kbase/cqasm-qubit-gate-operations/.
- ↑ "Microsoft.Quantum.Intrinsic namespace". Microsoft (Q#). 28 July 2023. https://docs.microsoft.com/en-us/qsharp/api/qsharp/microsoft.quantum.intrinsic.
- ↑ 10.0 10.1 Operations and Functions (Q# documentation)
- ↑ 11.0 11.1 Ömer, Bernhard (2 September 2009). "Structured Quantum Programming". Institute for Theoretical Physics, Vienna University of Technology. pp. 72, 92–107. http://tph.tuwien.ac.at/~oemer/doc/structquprog.pdf.
- ↑ 12.0 12.1 Ömer, Bernhard (29 Apr 2003). "Classical Concepts in Quantum Programming". International Journal of Theoretical Physics 44 (7): 943–955. doi:10.1007/s10773-005-7071-x.
- ↑ 13.0 13.1 13.2 13.3 Ömer, Bernhard (2000-01-20). Quantum Programming in QCL (PDF) (Thesis). Institute for Theoretical Physics, Vienna University of Technology. Archived from the original (PDF) on June 1, 2022. Retrieved 2021-05-24.
- ↑ 14.0 14.1 "A cryogenic CMOS chip for generating control signals for multiple qubits". Nature Electronics 4 (4): 64–70. 2021. doi:10.1038/s41928-020-00528-y.
- ↑ "TdgGate". https://qiskit.org/documentation/stubs/qiskit.circuit.library.TdgGate.html#qiskit.circuit.library.TdgGate. Qiskit online documentation.
- ↑ "T dagger Gate". https://www.quantum-inspire.com/kbase/t-dagger-gate/. cQASM online documentation.
- ↑ 17.0 17.1 Aharonov, Dorit (2003-01-09). "A Simple Proof that Toffoli and Hadamard are Quantum Universal". arXiv:quant-ph/0301040.
- ↑ Sawicki, Adam; Karnas, Katarzyna (2017-11-01). "Universality of Single-Qudit Gates" (in en). Annales Henri Poincaré 18 (11): 3515–3552. doi:10.1007/s00023-017-0604-z. ISSN 1424-0661. Bibcode: 2017AnHP...18.3515S.
- ↑ Sawicki, Adam; Mattioli, Lorenzo; Zimborás, Zoltán (2022-05-12). "Universality verification for a set of quantum gates". Physical Review A 105 (5). doi:10.1103/PhysRevA.105.052602. Bibcode: 2022PhRvA.105e2602S. https://link.aps.org/doi/10.1103/PhysRevA.105.052602.
- ↑ Williams, Colin P. (2011), Williams, Colin P., ed., "Quantum Gates", Explorations in Quantum Computing, Texts in Computer Science (London, England: Springer): pp. 51–122, doi:10.1007/978-1-84628-887-6_2, ISBN 978-1-84628-887-6
- ↑ Deutsch, David (September 8, 1989), "Quantum computational networks", Proc. R. Soc. Lond. A 425 (1989): 73–90, doi:10.1098/rspa.1989.0099, Bibcode: 1989RSPSA.425...73D
- ↑ Shi, Xiao-Feng (2018-05-22). "Deutsch, Toffoli, and cnot Gates via Rydberg Blockade of Neutral Atoms" (in en). Physical Review Applied 9 (5). doi:10.1103/PhysRevApplied.9.051001. ISSN 2331-7019. Bibcode: 2018PhRvP...9e1001S. https://link.aps.org/doi/10.1103/PhysRevApplied.9.051001.
- ↑ "I operation". 28 July 2023. https://docs.microsoft.com/en-us/qsharp/api/qsharp/microsoft.quantum.intrinsic.i.
- ↑ "IGate". https://qiskit.org/documentation/stubs/qiskit.circuit.library.IGate.html#qiskit.circuit.library.IGate. Qiskit online documentation.
- ↑ 25.0 25.1 Loss, Daniel; DiVincenzo, David P. (1998-01-01). "Quantum computation with quantum dots". Physical Review A 57 (1): 120–126. doi:10.1103/physreva.57.120. ISSN 1050-2947. Bibcode: 1998PhRvA..57..120L. Example in eq. 2.
- ↑ Raz, Ran (2002). "On the complexity of matrix product". Proceedings of the thiry-fourth annual ACM Symposium on Theory of Computing. pp. 144–151. doi:10.1145/509907.509932. ISBN 1-58113-495-9.
- ↑ "UnitaryGate § UnitaryGate adjoint()". https://docs.quantum.ibm.com/api/qiskit/qiskit.circuit.library.UnitaryGate#adjoint.
- ↑ Griffiths, D.J. (2008). Introduction to Elementary Particles (2nd ed.). John Wiley & Sons. pp. 115–121, 126. ISBN 978-3-527-40601-2.
- ↑ Albert, David (1994). Quantum mechanics and experience. Harvard University Press. p. 35. ISBN 0-674-74113-7.
- ↑ Carroll, Sean M. (2019). Spacetime and Geometry: An Introduction to General Relativity. Cambridge University Press. pp. 376–394. ISBN 978-1-108-48839-6.
- ↑ Wallace, David (2012). The emergent multiverse: Quantum theory according to the Everett Interpretation. Oxford University Press. ISBN 978-0-19-954696-1.
- ↑ Carroll, Sean M. (2019). Something deeply hidden: Quantum worlds and the emergence of spacetime. Penguin Random House. ISBN 978-1-5247-4301-7.
- ↑ Q# Online manual: Measurement
- ↑ Juan Yin; Yuan Cao; Yu-Huai Li; Sheng-Kai Liao; Liang Zhang; Ji-Gang Ren; Wen-Qi Cai; Wei-Yue Liu et al. (2017). "Satellite-based entanglement distribution over 1200 kilometers". Quantum Optics 356 (6343): 1140–1144. doi:10.1126/science.aan3211. PMID 28619937.
- ↑ Billings, Lee (23 April 2020). "China Shatters "Spooky Action at a Distance" Record, Preps for Quantum Internet". https://www.scientificamerican.com/article/china-shatters-ldquo-spooky-action-at-a-distance-rdquo-record-preps-for-quantum-internet/.
- ↑ Popkin, Gabriel (15 June 2017). "China's quantum satellite achieves 'spooky action' at record distance". https://www.science.org/content/article/china-s-quantum-satellite-achieves-spooky-action-record-distance.
- ↑ Aaronson, Scott (2009). "BQP and the Polynomial Hierarchy". arXiv:0910.4698 [quant-ph].
- ↑ Dawson, Christopher M.; Nielsen, Michael (2006-01-01). "The Solovay-Kitaev algorithm" (in EN). Quantum Information and Computation 6 (1): Section 5.1, equation 23. doi:10.26421/QIC6.1-6. https://dl.acm.org/doi/abs/10.5555/2011679.2011685.
- ↑ Matteo, Olivia Di (2016). "Parallelizing quantum circuit synthesis". Quantum Science and Technology 1 (1). doi:10.1088/2058-9565/1/1/015003. Bibcode: 2016QS&T....1a5003D.
- ↑ Aaronson, Scott (2002). "Quantum Lower Bound for Recursive Fourier Sampling". Quantum Information and Computation 3 (2): 165–174. doi:10.26421/QIC3.2-7. Bibcode: 2002quant.ph..9060A.
- ↑ Q# online manual: Quantum Memory Management
- ↑ Ryo, Asaka; Kazumitsu, Sakai; Ryoko, Yahagi (2020). "Quantum circuit for the fast Fourier transform". Quantum Information Processing 19 (277): 277. doi:10.1007/s11128-020-02776-5. Bibcode: 2020QuIP...19..277A. https://link.springer.com/article/10.1007/s11128-020-02776-5.
- ↑ Montaser, Rasha (2019). "New Design of Reversible Full Adder/Subtractor using R gate". International Journal of Theoretical Physics 58 (1): 167–183. doi:10.1007/s10773-018-3921-1. Bibcode: 2019IJTP...58..167M.
- ↑ QCL 0.6.4 source code, the file "lib/examples.qcl"
Sources
- Nielsen, Michael A.; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge, England: Cambridge University Press. ISBN 0-521-63235-8. OCLC 43641333.
- Williams, Colin P. (2011) (in en). Explorations in Quantum Computing. Springer. ISBN 978-1-84628-887-6.
- Yanofsky, Noson S.; Mannucci, Mirco (2013). Quantum computing for computer scientists. Cambridge University Press. ISBN 978-0-521-87996-5.
 |




