c-chart
| c-chart | |
|---|---|
| Originally proposed by | Walter A. Shewhart |
| Process observations | |
| Rational subgroup size | n > 1 |
| Measurement type | Number of nonconformances in a sample |
| Quality characteristic type | Attributes data |
| Underlying distribution | Poisson distribution |
| Performance | |
| Size of shift to detect | ≥ 1.5σ |
| Process variation chart | |
| Not applicable | |
| Process mean chart | |
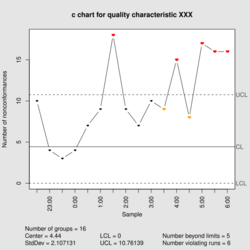 | |
| Center line | [math]\displaystyle{ \bar c = \frac {\sum_{i=1}^m \sum_{j=1}^n \mbox{no. of defects for } x_{ij}}{m} }[/math] |
| Control limits | [math]\displaystyle{ \bar c \pm 3\sqrt{\bar c} }[/math] |
| Plotted statistic | [math]\displaystyle{ \bar c_i = \sum_{j=1}^n \mbox{no. of defects for } x_{ij} }[/math] |
In statistical quality control, the c-chart is a type of control chart used to monitor "count"-type data, typically total number of nonconformities per unit.[1] It is also occasionally used to monitor the total number of events occurring in a given unit of time.
The c-chart differs from the p-chart in that it accounts for the possibility of more than one nonconformity per inspection unit, and that (unlike the p-chart and u-chart) it requires a fixed sample size. The p-chart models "pass"/"fail"-type inspection only, while the c-chart (and u-chart) give the ability to distinguish between (for example) 2 items which fail inspection because of one fault each and the same two items failing inspection with 5 faults each; in the former case, the p-chart will show two non-conformant items, while the c-chart will show 10 faults.
Nonconformities may also be tracked by type or location which can prove helpful in tracking down assignable causes.
Examples of processes suitable for monitoring with a c-chart include:
- Monitoring the number of voids per inspection unit in injection molding or casting processes
- Monitoring the number of discrete components that must be re-soldered per printed circuit board
- Monitoring the number of product returns per day
The Poisson distribution is the basis for the chart and requires the following assumptions:[2]
- The number of opportunities or potential locations for nonconformities is very large
- The probability of nonconformity at any location is small and constant
- The inspection procedure is same for each sample and is carried out consistently from sample to sample
The control limits for this chart type are [math]\displaystyle{ \bar c \pm 3\sqrt{\bar c} }[/math] where [math]\displaystyle{ \bar c }[/math] is the estimate of the long-term process mean established during control-chart setup.
See also
References
- ↑ "Counts Control Charts". NIST/Sematech Engineering Statistics Handbook. National Institute of Standards and Technology. http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc331.htm. Retrieved 2008-08-23.
- ↑ Montgomery, Douglas (2005). Introduction to Statistical Quality Control. Hoboken, New Jersey: John Wiley & Sons , Inc.. pp. 289. ISBN 978-0-471-65631-9. OCLC 56729567. http://www.eas.asu.edu/~masmlab/montgomery/. Retrieved 2008-08-23.
 |

