CYK algorithm

From HandWiki
Short description: Parsing algorithm for context-free grammars
Cocke–Younger–Kasami algorithm (CYK)
ClassParsing with context-free grammars
Data structureString
Worst-case performance[math]\displaystyle{ \mathcal{O}\left( n^3 \cdot \left| G \right| \right) }[/math], where:
  • [math]\displaystyle{ n }[/math] is length of the string
  • [math]\displaystyle{ |G| }[/math] is the size of the CNF grammar
Worst-case space complexity{{{space}}}

In computer science, the Cocke–Younger–Kasami algorithm (alternatively called CYK, or CKY) is a parsing algorithm for context-free grammars published by Itiroo Sakai in 1961.[1][2] The algorithm is named after some of its rediscoverers: John Cocke, Daniel Younger, Tadao Kasami, and Jacob T. Schwartz. It employs bottom-up parsing and dynamic programming.

The standard version of CYK operates only on context-free grammars given in Chomsky normal form (CNF). However any context-free grammar may be algorithmically transformed into a CNF grammar expressing the same language (Sipser 1997).

The importance of the CYK algorithm stems from its high efficiency in certain situations. Using big O notation, the worst case running time of CYK is [math]\displaystyle{ \mathcal{O}\left( n^3 \cdot \left| G \right| \right) }[/math], where [math]\displaystyle{ n }[/math] is the length of the parsed string and [math]\displaystyle{ \left| G \right| }[/math] is the size of the CNF grammar [math]\displaystyle{ G }[/math] (Hopcroft Ullman). This makes it one of the most efficient[citation needed] parsing algorithms in terms of worst-case asymptotic complexity, although other algorithms exist with better average running time in many practical scenarios.

Standard form

The dynamic programming algorithm requires the context-free grammar to be rendered into Chomsky normal form (CNF), because it tests for possibilities to split the current sequence into two smaller sequences. Any context-free grammar that does not generate the empty string can be represented in CNF using only production rules of the forms [math]\displaystyle{ A\rightarrow \alpha }[/math], [math]\displaystyle{ A\rightarrow B C }[/math], and [math]\displaystyle{ S\to \varepsilon }[/math] where [math]\displaystyle{ S }[/math] is the start symbol.[3]

Algorithm

As pseudocode

The algorithm in pseudocode is as follows: 

let the input be a string I consisting of n characters: a1 ... an.
let the grammar contain r nonterminal symbols R1 ... Rr, with start symbol R1.
let P[n,n,r] be an array of booleans. Initialize all elements of P to false.
let back[n,n,r] be an array of lists of backpointing triples. Initialize all elements of back to the empty list.

for each s = 1 to n
    for each unit production Rv → as
        set P[1,s,v] = true

for each l = 2 to n -- Length of span
    for each s = 1 to n-l+1 -- Start of span
        for each p = 1 to l-1 -- Partition of span
            for each production Ra    → Rb Rc
                if P[p,s,b] and P[l-p,s+p,c] then
                    set P[l,s,a] = true, 
                    append <p,b,c> to back[l,s,a]

if P[n,1,1] is true then
    I is member of language
    return back -- by retracing the steps through back, one can easily construct all possible parse trees of the string.
else
    return "not a member of language"

Probabilistic CYK (for finding the most probable parse)

Allows to recover the most probable parse given the probabilities of all productions. 

let the input be a string I consisting of n characters: a1 ... an.
let the grammar contain r nonterminal symbols R1 ... Rr, with start symbol R1.
let P[n,n,r] be an array of real numbers. Initialize all elements of P to zero.
let back[n,n,r] be an array of backpointing triples.
for each s = 1 to n
  for each unit production Rv →as
    set P[1,s,v] = Pr(Rv →as)
for each l = 2 to n -- Length of span
  for each s = 1 to n-l+1 -- Start of span
    for each p = 1 to l-1 -- Partition of span       
      for each production Ra → Rb Rc
        prob_splitting = Pr(Ra →Rb Rc) * P[p,s,b] * P[l-p,s+p,c]
        if prob_splitting > P[l,s,a] then 
          set P[l,s,a] = prob_splitting
          set back[l,s,a] = <p,b,c>

if P[n,1,1] > 0 then
    find the parse tree by retracing through back
    return the parse tree
else
    return "not a member of language"

As prose

In informal terms, this algorithm considers every possible substring of the input string and sets [math]\displaystyle{ P[l,s,v] }[/math] to be true if the substring of length [math]\displaystyle{ l }[/math] starting from [math]\displaystyle{ s }[/math] can be generated from the nonterminal [math]\displaystyle{ R_v }[/math]. Once it has considered substrings of length 1, it goes on to substrings of length 2, and so on. For substrings of length 2 and greater, it considers every possible partition of the substring into two parts, and checks to see if there is some production [math]\displaystyle{ A \to B \; C }[/math] such that [math]\displaystyle{ B }[/math] matches the first part and [math]\displaystyle{ C }[/math] matches the second part. If so, it records [math]\displaystyle{ A }[/math] as matching the whole substring. Once this process is completed, the input string is generated by the grammar if the substring containing the entire input string is matched by the start symbol.

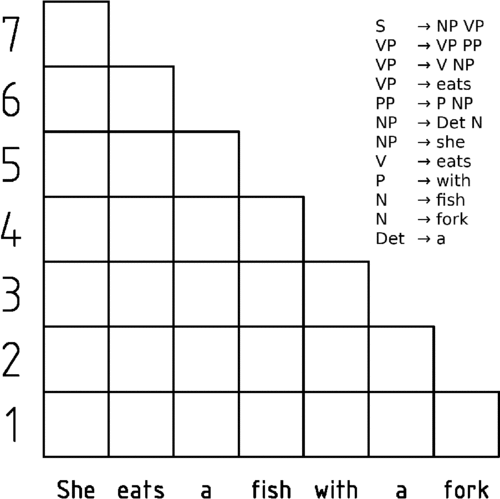
Example

Sentence parsing using the CYK algorithm

This is an example grammar:

[math]\displaystyle{ \begin{align} \ce{S} & \ \ce{-\gt NP\ VP}\\ \ce{VP} & \ \ce{-\gt VP\ PP}\\ \ce{VP} & \ \ce{-\gt V\ NP}\\ \ce{VP} & \ \ce{-\gt eats}\\ \ce{PP} & \ \ce{-\gt P\ NP}\\ \ce{NP} & \ \ce{-\gt Det\ N}\\ \ce{NP} & \ \ce{-\gt she}\\ \ce{V} & \ \ce{-\gt eats}\\ \ce{P} & \ \ce{-\gt with}\\ \ce{N} & \ \ce{-\gt fish}\\ \ce{N} & \ \ce{-\gt fork}\\ \ce{Det} & \ \ce{-\gt a} \end{align} }[/math]

Now the sentence she eats a fish with a fork is analyzed using the CYK algorithm. In the following table, in [math]\displaystyle{ P[i,j,k] }[/math], i is the number of the row (starting at the bottom at 1), and j is the number of the column (starting at the left at 1).

CYK table
S
VP
 
S
VP PP
S NP NP
NP V, VP Det. N P Det N
she eats a fish with a fork

For readability, the CYK table for P is represented here as a 2-dimensional matrix M containing a set of non-terminal symbols, such that Rk is in [math]\displaystyle{ M[i,j] }[/math] if, and only if, [math]\displaystyle{ P[i,j,k] }[/math]. In the above example, since a start symbol S is in [math]\displaystyle{ M[7,1] }[/math], the sentence can be generated by the grammar.

Extensions

Generating a parse tree

The above algorithm is a recognizer that will only determine if a sentence is in the language. It is simple to extend it into a parser that also constructs a parse tree, by storing parse tree nodes as elements of the array, instead of the boolean 1. The node is linked to the array elements that were used to produce it, so as to build the tree structure. Only one such node in each array element is needed if only one parse tree is to be produced. However, if all parse trees of an ambiguous sentence are to be kept, it is necessary to store in the array element a list of all the ways the corresponding node can be obtained in the parsing process. This is sometimes done with a second table B[n,n,r] of so-called backpointers. The end result is then a shared-forest of possible parse trees, where common trees parts are factored between the various parses. This shared forest can conveniently be read as an ambiguous grammar generating only the sentence parsed, but with the same ambiguity as the original grammar, and the same parse trees up to a very simple renaming of non-terminals, as shown by (Lang 1994).

Parsing non-CNF context-free grammars

As pointed out by (Lange Leiß), the drawback of all known transformations into Chomsky normal form is that they can lead to an undesirable bloat in grammar size. The size of a grammar is the sum of the sizes of its production rules, where the size of a rule is one plus the length of its right-hand side. Using [math]\displaystyle{ g }[/math] to denote the size of the original grammar, the size blow-up in the worst case may range from [math]\displaystyle{ g^2 }[/math] to [math]\displaystyle{ 2^{2 g} }[/math], depending on the transformation algorithm used. For the use in teaching, Lange and Leiß propose a slight generalization of the CYK algorithm, "without compromising efficiency of the algorithm, clarity of its presentation, or simplicity of proofs" (Lange Leiß).

Parsing weighted context-free grammars

It is also possible to extend the CYK algorithm to parse strings using weighted and stochastic context-free grammars. Weights (probabilities) are then stored in the table P instead of booleans, so P[i,j,A] will contain the minimum weight (maximum probability) that the substring from i to j can be derived from A. Further extensions of the algorithm allow all parses of a string to be enumerated from lowest to highest weight (highest to lowest probability).

Numerical stability

When the probabilistic CYK algorithm is applied to a long string, the splitting probability can become very small due to multiplying many probabilities together. This can be dealt with by summing log-probability instead of multiplying probabilities.

Valiant's algorithm

The worst case running time of CYK is [math]\displaystyle{ \Theta(n^3 \cdot |G|) }[/math], where n is the length of the parsed string and |G| is the size of the CNF grammar G. This makes it one of the most efficient algorithms for recognizing general context-free languages in practice. (Valiant 1975) gave an extension of the CYK algorithm. His algorithm computes the same parsing table as the CYK algorithm; yet he showed that algorithms for efficient multiplication of matrices with 0-1-entries can be utilized for performing this computation.

Using the Coppersmith–Winograd algorithm for multiplying these matrices, this gives an asymptotic worst-case running time of [math]\displaystyle{ O(n^{2.38} \cdot |G|) }[/math]. However, the constant term hidden by the Big O Notation is so large that the Coppersmith–Winograd algorithm is only worthwhile for matrices that are too large to handle on present-day computers (Knuth 1997), and this approach requires subtraction and so is only suitable for recognition. The dependence on efficient matrix multiplication cannot be avoided altogether: (Lee 2002) has proved that any parser for context-free grammars working in time [math]\displaystyle{ O(n^{3-\varepsilon} \cdot |G|) }[/math] can be effectively converted into an algorithm computing the product of [math]\displaystyle{ (n \times n) }[/math]-matrices with 0-1-entries in time [math]\displaystyle{ O(n^{3 - \varepsilon/3}) }[/math], and this was extended by Abboud et al.[4] to apply to a constant-size grammar.

See also

References

  1. ↑ Grune, Dick (2008). Parsing techniques : a practical guide (2nd ed.). New York: Springer. p. 579. ISBN 978-0-387-20248-8. 
  2. ↑ Itiroo Sakai, “Syntax in universal translation”. In Proceedings 1961 International Conference on Machine Translation of Languages and Applied Language Analysis, Her Majesty’s Stationery Office, London, p. 593-608, 1962.
  3. ↑ Sipser, Michael (2006). Introduction to the theory of computation (2nd ed.). Boston: Thomson Course Technology. Definition 2.8. ISBN 0-534-95097-3. OCLC 58544333. https://www.worldcat.org/oclc/58544333. 
  4. ↑ Abboud, Amir; Backurs, Arturs; Williams, Virginia Vassilevska (2015-11-05). "If the Current Clique Algorithms are Optimal, so is Valiant's Parser". arXiv:1504.01431 [cs.CC].

Sources

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=CYK_algorithm&oldid=3357738"