Context-free grammar
In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form
with a single nonterminal symbol, and a string of terminals and/or nonterminals ( can be empty). Regardless of which symbols surround it, the single nonterminal on the left hand side can always be replaced by on the right hand side. This distinguishes it from a context-sensitive grammar, which can have production rules in the form with a nonterminal symbol and , , and strings of terminal and/or nonterminal symbols.
A formal grammar is essentially a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the first rule in the picture,
replaces with . There can be multiple replacement rules for a given nonterminal symbol. The language generated by a grammar is the set of all strings of terminal symbols that can be derived, by repeated rule applications, from some particular nonterminal symbol ("start symbol"). Nonterminal symbols are used during the derivation process, but do not appear in its final result string.
Languages generated by context-free grammars are known as context-free languages (CFL). Different context-free grammars can generate the same context-free language. It is important to distinguish the properties of the language (intrinsic properties) from the properties of a particular grammar (extrinsic properties). The language equality question (do two given context-free grammars generate the same language?) is undecidable.
Context-free grammars arise in linguistics where they are used to describe the structure of sentences and words in a natural language, and they were invented by the linguist Noam Chomsky for this purpose. By contrast, in computer science, as the use of recursively-defined concepts increased, they were used more and more. In an early application, grammars are used to describe the structure of programming languages. In a newer application, they are used in an essential part of the Extensible Markup Language (XML) called the document type definition.[2]
In linguistics, some authors use the term phrase structure grammar to refer to context-free grammars, whereby phrase-structure grammars are distinct from dependency grammars. In computer science, a popular notation for context-free grammars is Backus–Naur form, or BNF.
Background
Since at least the time of the ancient Indian scholar Pāṇini, linguists have described the grammars of languages in terms of their block structure, and described how sentences are recursively built up from smaller phrases, and eventually individual words or word elements. An essential property of these block structures is that logical units never overlap. For example, the sentence:
- John, whose blue car was in the garage, walked to the grocery store.
can be logically parenthesized (with the logical metasymbols [ ]) as follows:
- [John[, [whose [blue car]] [was [in [the garage]]],]] [walked [to [the [grocery store]]]].
A context-free grammar provides a simple and mathematically precise mechanism for describing the methods by which phrases in some natural language are built from smaller blocks, capturing the "block structure" of sentences in a natural way. Its simplicity makes the formalism amenable to rigorous mathematical study. Important features of natural language syntax such as agreement and reference are not part of the context-free grammar, but the basic recursive structure of sentences, the way in which clauses nest inside other clauses, and the way in which lists of adjectives and adverbs are swallowed by nouns and verbs, is described exactly.
Context-free grammars are a special form of Semi-Thue systems that in their general form date back to the work of Axel Thue.
The formalism of context-free grammars was developed in the mid-1950s by Noam Chomsky,[3] and also their classification as a special type of formal grammar (which he called phrase-structure grammars).[4] Some authors, however, reserve the term for more restricted grammars in the Chomsky hierarchy: context-sensitive grammars or context-free grammars. In a broader sense, phrase structure grammars are also known as constituency grammars. The defining trait of phrase structure grammars is thus their adherence to the constituency relation, as opposed to the dependency relation of dependency grammars. In Chomsky's generative grammar framework, the syntax of natural language was described by context-free rules combined with transformation rules.[5]
Block structure was introduced into computer programming languages by the Algol project (1957–1960), which, as a consequence, also featured a context-free grammar to describe the resulting Algol syntax. This became a standard feature of computer languages, and the notation for grammars used in concrete descriptions of computer languages came to be known as Backus–Naur form, after two members of the Algol language design committee.[3] The "block structure" aspect that context-free grammars capture is so fundamental to grammar that the terms syntax and grammar are often identified with context-free grammar rules, especially in computer science. Formal constraints not captured by the grammar are then considered to be part of the "semantics" of the language.
Context-free grammars are simple enough to allow the construction of efficient parsing algorithms that, for a given string, determine whether and how it can be generated from the grammar. An Earley parser is an example of such an algorithm, while the widely used LR and LL parsers are simpler algorithms that deal only with more restrictive subsets of context-free grammars.
Formal definitions
A context-free grammar G is defined by the 4-tuple , where[6]
- V is a finite set; each element is called a nonterminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by G.
- Σ is a finite set of terminals, disjoint from V, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar G.
- R is a finite relation in , where the asterisk represents the Kleene star operation. The members of R are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a P)
- S is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of V.
Production rule notation
A production rule in R is formalized mathematically as a pair , where is a nonterminal and is a string of variables and/or terminals; rather than using ordered pair notation, production rules are usually written using an arrow operator with as its left hand side and β as its right hand side: .
It is allowed for β to be the empty string, and in this case it is customary to denote it by ε. The form is called an ε-production.[7]
It is common to list all right-hand sides for the same left-hand side on the same line, using | (the vertical bar) to separate them. Rules and can hence be written as . In this case, and are called the first and second alternative, respectively.
Rule application
For any strings , we say u directly yields v, written as , if with and such that and . Thus, v is a result of applying the rule to u.
Repetitive rule application
For any strings we say u yields v or v is derived from u if there is a positive integer k and strings such that . This relation is denoted , or in some textbooks. If , the relation holds. In other words, and are the reflexive transitive closure (allowing a string to yield itself) and the transitive closure (requiring at least one step) of , respectively.
Context-free language
The language of a grammar is the set
of all terminal-symbol strings derivable from the start symbol.
A language L is said to be a context-free language (CFL), if there exists a CFG G, such that .
Non-deterministic pushdown automata recognize exactly the context-free languages.
Examples
Words concatenated with their reverse
The grammar , with productions
- S → aSa,
- S → bSb,
- S → ε,
is context-free. It is not proper since it includes an ε-production. A typical derivation in this grammar is
- S → aSa → aaSaa → aabSbaa → aabbaa.
This makes it clear that . The language is context-free, however, it can be proved that it is not regular.
If the productions
- S → a,
- S → b,
are added, a context-free grammar for the set of all palindromes over the alphabet { a, b } is obtained.[8]
Well-formed parentheses
The canonical example of a context-free grammar is parenthesis matching, which is representative of the general case. There are two terminal symbols "(" and ")" and one nonterminal symbol S. The production rules are
- S → SS,
- S → (S),
- S → ()
The first rule allows the S symbol to multiply; the second rule allows the S symbol to become enclosed by matching parentheses; and the third rule terminates the recursion.[9]
Well-formed nested parentheses and square brackets
A second canonical example is two different kinds of matching nested parentheses, described by the productions:
- S → SS
- S → ()
- S → (S)
- S → []
- S → [S]
with terminal symbols [ ] ( ) and nonterminal S.
The following sequence can be derived in that grammar:
- ([ [ [ ()() [ ][ ] ] ]([ ]) ])
Matching pairs
In a context-free grammar, we can pair up characters the way we do with brackets. The simplest example:
- S → aSb
- S → ab
This grammar generates the language , which is not regular (according to the pumping lemma for regular languages).
The special character ε stands for the empty string. By changing the above grammar to
- S → aSb
- S → ε
we obtain a grammar generating the language instead. This differs only in that it contains the empty string while the original grammar did not.
Distinct number of a's and b's
A context-free grammar for the language consisting of all strings over {a,b} containing an unequal number of a's and b's:
- S → T | U
- T → VaT | VaV | TaV
- U → VbU | VbV | UbV
- V → aVbV | bVaV | ε
Here, the nonterminal T can generate all strings with more a's than b's, the nonterminal U generates all strings with more b's than a's and the nonterminal V generates all strings with an equal number of a's and b's. Omitting the third alternative in the rules for T and U does not restrict the grammar's language.
Second block of b's of double size
Another example of a non-regular language is . It is context-free as it can be generated by the following context-free grammar:
- S → bSbb | A
- A → aA | ε
First-order logic formulas
The formation rules for the terms and formulas of formal logic fit the definition of context-free grammar, except that the set of symbols may be infinite and there may be more than one start symbol.
Examples of languages that are not context free
In contrast to well-formed nested parentheses and square brackets in the previous section, there is no context-free grammar for generating all sequences of two different types of parentheses, each separately balanced disregarding the other, where the two types need not nest inside one another, for example:
- [ ( ] )
or
- [ [ [ [(((( ] ] ] ]))))(([ ))(([ ))([ )( ])( ])( ])
The fact that this language is not context free can be proven using pumping lemma for context-free languages and a proof by contradiction, observing that all words of the form should belong to the language. This language belongs instead to a more general class and can be described by a conjunctive grammar, which in turn also includes other non-context-free languages, such as the language of all words of the form .
Regular grammars
Every regular grammar is context-free, but not all context-free grammars are regular.[10] The following context-free grammar, for example, is also regular.
- S → a
- S → aS
- S → bS
The terminals here are a and b, while the only nonterminal is S. The language described is all nonempty strings of s and s that end in .
This grammar is regular: no rule has more than one nonterminal in its right-hand side, and each of these nonterminals is at the same end of the right-hand side.
Every regular grammar corresponds directly to a nondeterministic finite automaton, so we know that this is a regular language.
Using vertical bars, the grammar above can be described more tersely as follows:
- S → a | aS | bS
Derivations and syntax trees
A derivation of a string for a grammar is a sequence of grammar rule applications that transform the start symbol into the string. A derivation proves that the string belongs to the grammar's language.
A derivation is fully determined by giving, for each step:
- the rule applied in that step
- the occurrence of its left-hand side to which it is applied
For clarity, the intermediate string is usually given as well.
For instance, with the grammar:
- S → S + S
- S → 1
- S → a
the string
- 1 + 1 + a
can be derived from the start symbol S with the following derivation:
- S
- → S + S (by rule 1. on S)
- → S + S + S (by rule 1. on the second S)
- → 1 + S + S (by rule 2. on the first S)
- → 1 + 1 + S (by rule 2. on the second S)
- → 1 + 1 + a (by rule 3. on the third S)
Often, a strategy is followed that deterministically chooses the next nonterminal to rewrite:
- in a leftmost derivation, it is always the leftmost nonterminal;
- in a rightmost derivation, it is always the rightmost nonterminal.
Given such a strategy, a derivation is completely determined by the sequence of rules applied. For instance, one leftmost derivation of the same string is
- S
- → S + S (by rule 1 on the leftmost S)
- → 1 + S (by rule 2 on the leftmost S)
- → 1 + S + S (by rule 1 on the leftmost S)
- → 1 + 1 + S (by rule 2 on the leftmost S)
- → 1 + 1 + a (by rule 3 on the leftmost S),
which can be summarized as
- rule 1
- rule 2
- rule 1
- rule 2
- rule 3.
One rightmost derivation is:
- S
- → S + S (by rule 1 on the rightmost S)
- → S + S + S (by rule 1 on the rightmost S)
- → S + S + a (by rule 3 on the rightmost S)
- → S + 1 + a (by rule 2 on the rightmost S)
- → 1 + 1 + a (by rule 2 on the rightmost S),
which can be summarized as
- rule 1
- rule 1
- rule 3
- rule 2
- rule 2.
The distinction between leftmost derivation and rightmost derivation is important because in most parsers the transformation of the input is defined by giving a piece of code for every grammar rule that is executed whenever the rule is applied. Therefore, it is important to know whether the parser determines a leftmost or a rightmost derivation because this determines the order in which the pieces of code will be executed. See for an example LL parsers and LR parsers.
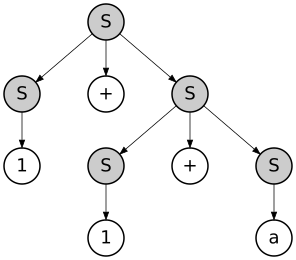
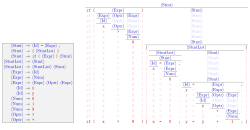
A derivation also imposes in some sense a hierarchical structure on the string that is derived. For example, if the string "1 + 1 + a" is derived according to the leftmost derivation outlined above, the structure of the string would be:
- {{1}S + {{1}S + {a}S}S}S
where {...}S indicates a substring recognized as belonging to S. This hierarchy can also be seen as a tree:
This tree is called a parse tree or "concrete syntax tree" of the string, by contrast with the abstract syntax tree. In this case the presented leftmost and the rightmost derivations define the same parse tree; however, there is another rightmost derivation of the same string
- S
- → S + S (by rule 1 on the rightmost S)
- → S + a (by rule 3 on the rightmost S)
- → S + S + a (by rule 1 on the rightmost S)
- → S + 1 + a (by rule 2 on the rightmost S)
- → 1 + 1 + a (by rule 2 on the rightmost S),
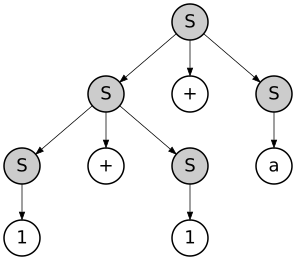
which defines a string with a different structure
- {{{1}S + {1}S}S + {a}S}S
and a different parse tree:
Note however that both parse trees can be obtained by both leftmost and rightmost derivations. For example, the last tree can be obtained with the leftmost derivation as follows:
- S
- → S + S (by rule 1 on the leftmost S)
- → S + S + S (by rule 1 on the leftmost S)
- → 1 + S + S (by rule 2 on the leftmost S)
- → 1 + 1 + S (by rule 2 on the leftmost S)
- → 1 + 1 + a (by rule 3 on the leftmost S),
If a string in the language of the grammar has more than one parsing tree, then the grammar is said to be an ambiguous grammar. Such grammars are usually hard to parse because the parser cannot always decide which grammar rule it has to apply. Usually, ambiguity is a feature of the grammar, not the language, and an unambiguous grammar can be found that generates the same context-free language. However, there are certain languages that can only be generated by ambiguous grammars; such languages are called inherently ambiguous languages.
Example: Algebraic expressions
Here is a context-free grammar for syntactically correct infix algebraic expressions in the variables x, y and z:
- S → x
- S → y
- S → z
- S → S + S
- S → S – S
- S → S * S
- S → S / S
- S → (S)
This grammar can, for example, generate the string
- (x + y) * x – z * y / (x + x)
as follows:
- S
- → S – S (by rule 5)
- → S * S – S (by rule 6, applied to the leftmost S)
- → S * S – S / S (by rule 7, applied to the rightmost S)
- → (S) * S – S / S (by rule 8, applied to the leftmost S)
- → (S) * S – S / (S) (by rule 8, applied to the rightmost S)
- → (S + S) * S – S / (S) (by rule 4, applied to the leftmost S)
- → (S + S) * S – S * S / (S) (by rule 6, applied to the fourth S)
- → (S + S) * S – S * S / (S + S) (by rule 4, applied to the rightmost S)
- → (x + S) * S – S * S / (S + S) (etc.)
- → (x + y) * S – S * S / (S + S)
- → (x + y) * x – S * S / (S + S)
- → (x + y) * x – z * S / (S + S)
- → (x + y) * x – z * y / (S + S)
- → (x + y) * x – z * y / (x + S)
- → (x + y) * x – z * y / (x + x)
Note that many choices were made underway as to which rewrite was going to be performed next. These choices look quite arbitrary. As a matter of fact, they are, in the sense that the string finally generated is always the same. For example, the second and third rewrites
- → S * S – S (by rule 6, applied to the leftmost S)
- → S * S – S / S (by rule 7, applied to the rightmost S)
could be done in the opposite order:
- → S – S / S (by rule 7, applied to the rightmost S)
- → S * S – S / S (by rule 6, applied to the leftmost S)
Also, many choices were made on which rule to apply to each selected S. Changing the choices made and not only the order they were made in usually affects which terminal string comes out at the end.
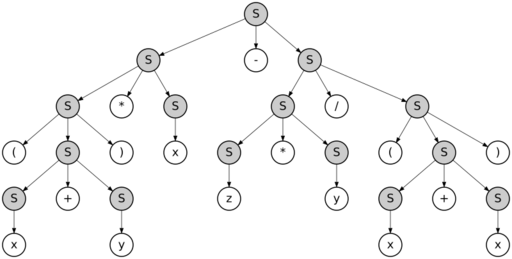
Let's look at this in more detail. Consider the parse tree of this derivation:
Starting at the top, step by step, an S in the tree is expanded, until no more unexpanded Ses (nonterminals) remain. Picking a different order of expansion will produce a different derivation, but the same parse tree. The parse tree will only change if we pick a different rule to apply at some position in the tree.
But can a different parse tree still produce the same terminal string, which is (x + y) * x – z * y / (x + x) in this case? Yes, for this particular grammar, this is possible. Grammars with this property are called ambiguous.
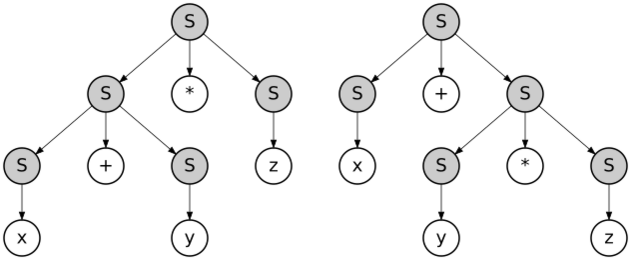
For example, x + y * z can be produced with these two different parse trees:
However, the language described by this grammar is not inherently ambiguous: an alternative, unambiguous grammar can be given for the language, for example:
- T → x
- T → y
- T → z
- S → S + T
- S → S – T
- S → S * T
- S → S / T
- T → (S)
- S → T,
once again picking S as the start symbol. This alternative grammar will produce x + y * z with a parse tree similar to the left one above, i.e. implicitly assuming the association (x + y) * z, which does not follow standard order of operations. More elaborate, unambiguous and context-free grammars can be constructed that produce parse trees that obey all desired operator precedence and associativity rules.
Normal forms
Every context-free grammar with no ε-production has an equivalent grammar in Chomsky normal form, and a grammar in Greibach normal form. "Equivalent" here means that the two grammars generate the same language.
The especially simple form of production rules in Chomsky normal form grammars has both theoretical and practical implications. For instance, given a context-free grammar, one can use the Chomsky normal form to construct a polynomial-time algorithm that decides whether a given string is in the language represented by that grammar or not (the CYK algorithm).
Closure properties
Context-free languages are closed under the various operations, that is, if the languages K and L are context-free, so is the result of the following operations:
- union K ∪ L; concatenation K ∘ L; Kleene star L*[11]
- substitution (in particular homomorphism)[12]
- inverse homomorphism[13]
- intersection with a regular language[14]
They are not closed under general intersection (hence neither under complementation) and set difference.[15]
Decidable problems
The following are some decidable problems about context-free grammars.
Parsing
The parsing problem, checking whether a given word belongs to the language given by a context-free grammar, is decidable, using one of the general-purpose parsing algorithms:
- CYK algorithm (for grammars in Chomsky normal form)
- Earley parser
- GLR parser
- LL parser (only for the proper subclass of for LL(k) grammars)
Context-free parsing for Chomsky normal form grammars was shown by Leslie G. Valiant to be reducible to boolean matrix multiplication, thus inheriting its complexity upper bound of O(n2.3728639).[16][17][note 1] Conversely, Lillian Lee has shown O(n3−ε) boolean matrix multiplication to be reducible to O(n3−3ε) CFG parsing, thus establishing some kind of lower bound for the latter.[18]
Reachability, productiveness, nullability
| Example grammar: | |||
|---|---|---|---|
| S → Bb | Cc | Ee | |||
| B → Bb | b | |||
| C → C | |||
| D → Bd | Cd | d | |||
| E → Ee | |||
A nonterminal symbol is called productive, or generating, if there is a derivation for some string of terminal symbols. is called reachable if there is a derivation for some strings of nonterminal and terminal symbols from the start symbol. is called useless if it is unreachable or unproductive. is called nullable if there is a derivation . A rule is called an ε-production. A derivation is called a cycle.
Algorithms are known to eliminate from a given grammar, without changing its generated language,
- unproductive symbols,[19][note 2]
- unreachable symbols,[21][22]
- ε-productions, with one possible exception,[note 3][23] and
- cycles.[note 4]
In particular, an alternative containing a useless nonterminal symbol can be deleted from the right-hand side of a rule. Such rules and alternatives are called useless.[24]
In the depicted example grammar, the nonterminal D is unreachable, and E is unproductive, while C → C causes a cycle. Hence, omitting the last three rules does not change the language generated by the grammar, nor does omitting the alternatives "| Cc | Ee" from the right-hand side of the rule for S.
A context-free grammar is said to be proper if it has neither useless symbols nor ε-productions nor cycles.[25] Combining the above algorithms, every context-free grammar not generating ε can be transformed into a weakly equivalent proper one.
Regularity and LL(k) checks
It is decidable whether a given grammar is a regular grammar,[26] as well as whether it is an LL(k) grammar for a given k≥0.[27]: 233 If k is not given, the latter problem is undecidable.[27]: 252
Given a context-free grammar, it is not decidable whether its language is regular,[28] nor whether it is an LL(k) language for a given k.[27]: 254
Emptiness and finiteness
There are algorithms to decide whether the language of a given context-free grammar is empty, as well as whether it is finite.[29]
Undecidable problems
Some questions that are undecidable for wider classes of grammars become decidable for context-free grammars; e.g. the emptiness problem (whether the grammar generates any terminal strings at all), is undecidable for context-sensitive grammars, but decidable for context-free grammars.
However, many problems are undecidable even for context-free grammars; the most prominent ones are handled in the following.
Universality
Given a CFG, does it generate the language of all strings over the alphabet of terminal symbols used in its rules?[30][31]
A reduction can be demonstrated to this problem from the well-known undecidable problem of determining whether a Turing machine accepts a particular input (the halting problem). The reduction uses the concept of a computation history, a string describing an entire computation of a Turing machine. A CFG can be constructed that generates all strings that are not accepting computation histories for a particular Turing machine on a particular input, and thus it will accept all strings only if the machine does not accept that input.
Language equality
Given two CFGs, do they generate the same language?[31][32]
The undecidability of this problem is a direct consequence of the previous: it is impossible to even decide whether a CFG is equivalent to the trivial CFG defining the language of all strings.
Language inclusion
Given two CFGs, can the first one generate all strings that the second one can generate?[31][32]
If this problem was decidable, then language equality could be decided too: two CFGs G1 and G2 generate the same language if L(G1) is a subset of L(G2) and L(G2) is a subset of L(G1).
Being in a lower or higher level of the Chomsky hierarchy
Using Greibach's theorem, it can be shown that the two following problems are undecidable:
- Given a context-sensitive grammar, does it describe a context-free language?
- Given a context-free grammar, does it describe a regular language?[31][32]
Grammar ambiguity
Given a CFG, is it ambiguous?
The undecidability of this problem follows from the fact that if an algorithm to determine ambiguity existed, the Post correspondence problem could be decided, which is known to be undecidable.[33] This may be proved by Ogden's lemma.[34]
Language disjointness
Given two CFGs, is there any string derivable from both grammars?
If this problem was decidable, the undecidable Post correspondence problem could be decided, too: given strings over some alphabet , let the grammar consist of the rule
- ;
where denotes the reversed string and does not occur among the ; and let grammar consist of the rule
- ;
Then the Post problem given by has a solution if and only if and share a derivable string.
Extensions
An obvious way to extend the context-free grammar formalism is to allow nonterminals to have arguments, the values of which are passed along within the rules. This allows natural language features such as agreement and reference, and programming language analogs such as the correct use and definition of identifiers, to be expressed in a natural way. E.g. we can now easily express that in English sentences, the subject and verb must agree in number. In computer science, examples of this approach include affix grammars, attribute grammars, indexed grammars, and Van Wijngaarden two-level grammars. Similar extensions exist in linguistics.
An extended context-free grammar (or regular right part grammar) is one in which the right-hand side of the production rules is allowed to be a regular expression over the grammar's terminals and nonterminals. Extended context-free grammars describe exactly the context-free languages.[35]
Another extension is to allow additional terminal symbols to appear at the left-hand side of rules, constraining their application. This produces the formalism of context-sensitive grammars.
Subclasses
There are a number of important subclasses of the context-free grammars:
- LR(k) grammars (also known as deterministic context-free grammars) allow parsing (string recognition) with deterministic pushdown automata (PDA), but they can only describe deterministic context-free languages.
- Simple LR, Look-Ahead LR grammars are subclasses that allow further simplification of parsing. SLR and LALR are recognized using the same PDA as LR, but with simpler tables, in most cases.
- LL(k) and LL(*) grammars allow parsing by direct construction of a leftmost derivation as described above, and describe even fewer languages.
- Simple grammars are a subclass of the LL(1) grammars mostly interesting for its theoretical property that language equality of simple grammars is decidable, while language inclusion is not.
- Bracketed grammars have the property that the terminal symbols are divided into left and right bracket pairs that always match up in rules.
- Linear grammars have no rules with more than one nonterminal on the right-hand side.
- Regular grammars are a subclass of the linear grammars and describe the regular languages, i.e. they correspond to finite automata and regular expressions.
LR parsing extends LL parsing to support a larger range of grammars; in turn, generalized LR parsing extends LR parsing to support arbitrary context-free grammars. On LL grammars and LR grammars, it essentially performs LL parsing and LR parsing, respectively, while on nondeterministic grammars, it is as efficient as can be expected. Although GLR parsing was developed in the 1980s, many new language definitions and parser generators continue to be based on LL, LALR or LR parsing up to the present day.
Linguistic applications
Chomsky initially hoped to overcome the limitations of context-free grammars by adding transformation rules.[4]
Such rules are another standard device in traditional linguistics; e.g. passivization in English. Much of generative grammar has been devoted to finding ways of refining the descriptive mechanisms of phrase-structure grammar and transformation rules such that exactly the kinds of things can be expressed that natural language actually allows. Allowing arbitrary transformations does not meet that goal: they are much too powerful, being Turing complete unless significant restrictions are added (e.g. no transformations that introduce and then rewrite symbols in a context-free fashion).
Chomsky's general position regarding the non-context-freeness of natural language has held up since then,[36] although his specific examples regarding the inadequacy of context-free grammars in terms of their weak generative capacity were later disproved.[37] Gerald Gazdar and Geoffrey Pullum have argued that despite a few non-context-free constructions in natural language (such as cross-serial dependencies in Swiss German[36] and reduplication in Bambara[38]), the vast majority of forms in natural language are indeed context-free.[37]
See also
- Parsing expression grammar
- Stochastic context-free grammar
- Algorithms for context-free grammar generation
- Pumping lemma for context-free languages
References
- ↑ Brian W. Kernighan and Dennis M. Ritchie (Apr 1988). The C Programming Language. Prentice Hall Software Series (2nd ed.). Englewood Cliffs/NJ: Prentice Hall. ISBN 0131103628. Here: App.A
- ↑ Introduction to Automata Theory, Languages, and Computation, John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman, Addison Wesley, 2001, p.191
- ↑ 3.0 3.1 (Hopcroft Ullman), p. 106.
- ↑ 4.0 4.1 Chomsky, Noam (Sep 1956), "Three models for the description of language", IEEE Transactions on Information Theory 2 (3): 113–124, doi:10.1109/TIT.1956.1056813
- ↑ Jurafsky, Daniel; Martin, James H. (29 December 2021). "Constituency Grammars". https://web.stanford.edu/~jurafsky/slp3/12.pdf.
- ↑ The notation here is that of (Sipser 1997), p. 94. (Hopcroft Ullman) (p. 79) define context-free grammars as 4-tuples in the same way, but with different variable names.
- ↑ (Hopcroft Ullman), pp. 90–92.
- ↑ (Hopcroft Ullman), Exercise 4.1a, p. 103.
- ↑ (Hopcroft Ullman), Exercise 4.1b, p. 103.
- ↑ Aho, Alfred Vaino; Lam, Monica S.; Sethi, Ravi; Ullman, Jeffrey David (2007). "4.2.7 Context-Free Grammars Versus Regular Expressions" (in en). Compilers: Principles, Techniques, & Tools (2nd ed.). Boston, MA USA: Pearson Addison-Wesley. pp. 205–206. ISBN 9780321486813. https://www.pearson.com/us/higher-education/program/Aho-Compilers-Principles-Techniques-and-Tools-2nd-Edition/PGM167067.html. "Every construct that can be described by a regular expression can be described by a [context-free] grammar, but not vice-versa."
- ↑ Hopcroft & Ullman (1979), p.131, Theorem 6.1
- ↑ Hopcroft & Ullman (1979), pp.131–132, Theorem 6.2
- ↑ Hopcroft & Ullman (1979), pp.132–134, Theorem 6.3
- ↑ Hopcroft & Ullman (1979), pp.135–136, Theorem 6.5
- ↑ Hopcroft & Ullman (1979), pp.134–135, Theorem 6.4
- ↑ Leslie Valiant (Jan 1974). General context-free recognition in less than cubic time (Technical report). Carnegie Mellon University. p. 11.
- ↑ Leslie G. Valiant (1975). "General context-free recognition in less than cubic time". Journal of Computer and System Sciences 10 (2): 308–315. doi:10.1016/s0022-0000(75)80046-8.
- ↑ Lillian Lee (2002). "Fast Context-Free Grammar Parsing Requires Fast Boolean Matrix Multiplication". J ACM 49 (1): 1–15. doi:10.1145/505241.505242. http://www.cs.cornell.edu/home/llee/papers/bmmcfl-jacm.pdf.
- ↑ (Hopcroft Ullman), Lemma 4.1, p. 88.
- ↑ Aiken, A.; Murphy, B. (1991). "Implementing Regular Tree Expressions". pp. 427–447.; here: Sect.4
- ↑ (Hopcroft Ullman), Lemma 4.2, p. 89.
- ↑ (Hopcroft Motwani), Theorem 7.2, Sect.7.1, p.255ff
- ↑ (Hopcroft Ullman), Theorem 4.3, p. 90.
- ↑ John E. Hopcroft; Rajeev Motwani; Jeffrey D. Ullman (2003). Introduction to Automata Theory, Languages, and Computation. Addison Wesley.; here: Sect.7.1.1, p.256
- ↑ Nijholt, Anton (1980), Context-free grammars: covers, normal forms, and parsing, Lecture Notes in Computer Science, 93, Springer, p. 8, ISBN 978-3-540-10245-8.
- ↑ This is easy to see from the grammar definitions.
- ↑ 27.0 27.1 27.2 D.J. Rosenkrantz and R.E. Stearns (1970). "Properties of Deterministic Top Down Grammars". Information and Control 17 (3): 226–256. doi:10.1016/S0019-9958(70)90446-8.
- ↑ (Hopcroft Ullman), Exercise 8.10a, p. 214. The problem remains undecidable even if the language is produced by a "linear" context-free grammar (i.e., with at most one nonterminal in each rule's right-hand side, cf. Exercise 4.20, p. 105).
- ↑ Hopcroft & Ullman (1979), pp.137–138, Theorem 6.6
- ↑ (Sipser 1997), Theorem 5.10, p. 181.
- ↑ 31.0 31.1 31.2 31.3 (Hopcroft Ullman), p. 281.
- ↑ 32.0 32.1 32.2 Hazewinkel, Michiel (1994), Encyclopaedia of mathematics: an updated and annotated translation of the Soviet "Mathematical Encyclopaedia", Springer, Vol. IV, p. 56, ISBN 978-1-55608-003-6, https://books.google.com/books?id=s9F71NJxwzoC&pg=PA56.
- ↑ (Hopcroft Ullman)
- ↑ Ogden, William (September 1968). "A helpful result for proving inherent ambiguity". Mathematical Systems Theory 2 (3): 191–194. doi:10.1007/bf01694004. ISSN 0025-5661. http://dx.doi.org/10.1007/bf01694004. Here: p.4
- ↑ Norvell, Theodore. "A Short Introduction to Regular Expressions and Context-Free Grammars". pp. 4. http://www.engr.mun.ca/~theo/Courses/fm/pub/context-free.pdf.
- ↑ 36.0 36.1 Shieber, Stuart (1985), "Evidence against the context-freeness of natural language", Linguistics and Philosophy 8 (3): 333–343, doi:10.1007/BF00630917, http://www.eecs.harvard.edu/~shieber/Biblio/Papers/shieber85.pdf.
- ↑ 37.0 37.1 Pullum, Geoffrey K.; Gerald Gazdar (1982), "Natural languages and context-free languages", Linguistics and Philosophy 4 (4): 471–504, doi:10.1007/BF00360802.
- ↑ Culy, Christopher (1985), "The Complexity of the Vocabulary of Bambara", Linguistics and Philosophy 8 (3): 345–351, doi:10.1007/BF00630918.
Notes
- ↑ In Valiant's papers, O(n2.81) is given, the then best known upper bound. See Matrix multiplication for bound improvements since then.
- ↑ For regular tree grammars, Aiken and Murphy give a fixpoint algorithm to detect unproductive nonterminals.[20]
- ↑ If the grammar can generate , a rule cannot be avoided.
- ↑ This is a consequence of the unit-production elimination theorem in Hopcroft & Ullman (1979), p.91, Theorem 4.4
Further reading
- Hopcroft, John E.; Ullman, Jeffrey D. (1979), Introduction to Automata Theory, Languages, and Computation, Addison-Wesley. Chapter 4: Context-Free Grammars, pp. 77–106; Chapter 6: Properties of Context-Free Languages, pp. 125–137.
- Hopcroft; Motwani, Rajeev; Ullman, Jeffrey D. (2003). Introduction to automata theory, languages, and computation (2nd ed.). Upper Saddle River: Pearson Education International. ISBN 978-0321210296.
- Sipser, Michael (1997), Introduction to the Theory of Computation, PWS Publishing, ISBN 978-0-534-94728-6, https://archive.org/details/introductiontoth00sips. Chapter 2: Context-Free Grammars, pp. 91–122; Section 4.1.2: Decidable problems concerning context-free languages, pp. 156–159; Section 5.1.1: Reductions via computation histories: pp. 176–183.
- J. Berstel, L. Boasson (1990). Jan van Leeuwen. ed. Context-Free Languages. Handbook of Theoretical Computer Science. B. Elsevier. pp. 59–102.
External links
- Computer programmers may find the stack exchange answer to be useful.
- CFG Developer created by Christopher Wong at Stanford University in 2014; modified by Kevin Gibbons in 2015.
 |