Camassa–Holm equation

From HandWiki
Interaction of two peakons — which are sharp-crested soliton solutions to the Camassa–Holm equation. The wave profile (solid curve) is formed by the simple linear addition of two peakons (dashed curves):
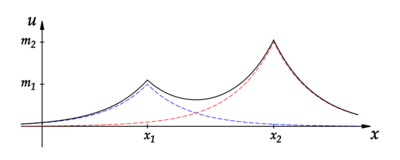
[math]\displaystyle{ u = m_1 \, e^{-|x-x_1|} + m_2 \, e^{-|x-x_2|}. }[/math]
The evolution of the individual peakon positions [math]\displaystyle{ x_1(t) }[/math] and [math]\displaystyle{ x_2(t) }[/math], as well as the evolution of the peakon amplitudes [math]\displaystyle{ m_1(t) }[/math] and [math]\displaystyle{ m_2(t), }[/math] is however less trivial: this is determined in a non-linear fashion by the interaction.

In fluid dynamics, the Camassa–Holm equation is the integrable, dimensionless and non-linear partial differential equation

[math]\displaystyle{ u_t + 2\kappa u_x - u_{xxt} + 3 u u_x = 2 u_x u_{xx} + u u_{xxx}. \, }[/math]

The equation was introduced by Roberto Camassa and Darryl Holm[1] as a bi-Hamiltonian model for waves in shallow water, and in this context the parameter κ is positive and the solitary wave solutions are smooth solitons.

In the special case that κ is equal to zero, the Camassa–Holm equation has peakon solutions: solitons with a sharp peak, so with a discontinuity at the peak in the wave slope.

Relation to waves in shallow water

The Camassa–Holm equation can be written as the system of equations:[2]

[math]\displaystyle{ \begin{align} u_t + u u_x + p_x &= 0, \\ p - p_{xx} &= 2 \kappa u + u^2 + \frac{1}{2} \left( u_x \right)^2, \end{align} }[/math]

with p the (dimensionless) pressure or surface elevation. This shows that the Camassa–Holm equation is a model for shallow water waves with non-hydrostatic pressure and a water layer on a horizontal bed.

The linear dispersion characteristics of the Camassa–Holm equation are:

[math]\displaystyle{ \omega = 2\kappa \frac{k}{1+k^2}, }[/math]

with ω the angular frequency and k the wavenumber. Not surprisingly, this is of similar form as the one for the Korteweg–de Vries equation, provided κ is non-zero. For κ equal to zero, the Camassa–Holm equation has no frequency dispersion — moreover, the linear phase speed is zero for this case. As a result, κ is the phase speed for the long-wave limit of k approaching zero, and the Camassa–Holm equation is (if κ is non-zero) a model for one-directional wave propagation like the Korteweg–de Vries equation.

Hamiltonian structure

Introducing the momentum m as

[math]\displaystyle{ m = u - u_{xx} + \kappa, \, }[/math]

then two compatible Hamiltonian descriptions of the Camassa–Holm equation are:[3]

[math]\displaystyle{ \begin{align} m_t &= -\mathcal{D}_1 \frac{\delta \mathcal{H}_1}{\delta m} & & \text{ with }& \mathcal{D}_1 &= m \frac{\partial}{\partial x} + \frac{\partial}{\partial x} m & \text{ and } \mathcal{H}_1 &= \frac{1}{2} \int u^2 + \left(u_x\right)^2\; \text{d}x, \\ m_t &= -\mathcal{D}_2 \frac{\delta \mathcal{H}_2}{\delta m} & & \text{ with }& \mathcal{D}_2 &= \frac{\partial}{\partial x} - \frac{\partial^3}{\partial x^3} & \text{ and } \mathcal{H}_2 &= \frac{1}{2} \int u^3 + u \left(u_{x}\right)^2 - \kappa u^2\; \text{d}x. \end{align} }[/math]

Integrability

The Camassa–Holm equation is an integrable system. Integrability means that there is a change of variables (action-angle variables) such that the evolution equation in the new variables is equivalent to a linear flow at constant speed. This change of variables is achieved by studying an associated isospectral/scattering problem, and is reminiscent of the fact that integrable classical Hamiltonian systems are equivalent to linear flows at constant speed on tori. The Camassa–Holm equation is integrable provided that the momentum

[math]\displaystyle{ m= u-u_{xx}+ \kappa \, }[/math]

is positive — see [4] and [5] for a detailed description of the spectrum associated to the isospectral problem,[4] for the inverse spectral problem in the case of spatially periodic smooth solutions, and [6] for the inverse scattering approach in the case of smooth solutions that decay at infinity.

Exact solutions

Traveling waves are solutions of the form

[math]\displaystyle{ u(t,x)=f(x-ct) \, }[/math]

representing waves of permanent shape f that propagate at constant speed c. These waves are called solitary waves if they are localized disturbances, that is, if the wave profile f decays at infinity. If the solitary waves retain their shape and speed after interacting with other waves of the same type, we say that the solitary waves are solitons. There is a close connection between integrability and solitons.[7] In the limiting case when κ = 0 the solitons become peaked (shaped like the graph of the function f(x) = e−|x|), and they are then called peakons. It is possible to provide explicit formulas for the peakon interactions, visualizing thus the fact that they are solitons.[8] For the smooth solitons the soliton interactions are less elegant.[9] This is due in part to the fact that, unlike the peakons, the smooth solitons are relatively easy to describe qualitatively — they are smooth, decaying exponentially fast at infinity, symmetric with respect to the crest, and with two inflection points[10] — but explicit formulas are not available. Notice also that the solitary waves are orbitally stable i.e. their shape is stable under small perturbations, both for the smooth solitons[10] and for the peakons.[11]

Wave breaking

The Camassa–Holm equation models breaking waves: a smooth initial profile with sufficient decay at infinity develops into either a wave that exists for all times or into a breaking wave (wave breaking[12] being characterized by the fact that the solution remains bounded but its slope becomes unbounded in finite time). The fact that the equations admits solutions of this type was discovered by Camassa and Holm[1] and these considerations were subsequently put on a firm mathematical basis.[13] It is known that the only way singularities can occur in solutions is in the form of breaking waves.[14][15] Moreover, from the knowledge of a smooth initial profile it is possible to predict (via a necessary and sufficient condition) whether wave breaking occurs or not.[16] As for the continuation of solutions after wave breaking, two scenarios are possible: the conservative case[17] and the dissipative case[18] (with the first characterized by conservation of the energy, while the dissipative scenario accounts for loss of energy due to breaking).

Long-time asymptotics

It can be shown that for sufficiently fast decaying smooth initial conditions with positive momentum splits into a finite number and solitons plus a decaying dispersive part. More precisely, one can show the following for [math]\displaystyle{ \kappa\gt 0 }[/math]:[19] Abbreviate [math]\displaystyle{ c =x / (\kappa t) }[/math]. In the soliton region [math]\displaystyle{ c\gt 2 }[/math] the solutions splits into a finite linear combination solitons. In the region [math]\displaystyle{ 0\lt c\lt 2 }[/math] the solution is asymptotically given by a modulated sine function whose amplitude decays like [math]\displaystyle{ t^{-1/2} }[/math]. In the region [math]\displaystyle{ -1/4\lt c\lt 0 }[/math] the solution is asymptotically given by a sum of two modulated sine function as in the previous case. In the region [math]\displaystyle{ c\lt -1/4 }[/math] the solution decays rapidly. In the case [math]\displaystyle{ \kappa=0 }[/math] the solution splits into an infinite linear combination of peakons[20] (as previously conjectured[21]).

Geometric formulation

In the spatially periodic case, the Camassa–Holm equation can be given the following geometric interpretation. The group [math]\displaystyle{ \mathrm{Diff}(S^1) }[/math] of diffeomorphisms of the unit circle [math]\displaystyle{ S^1 }[/math] is an infinite-dimensional Lie group whose Lie algebra [math]\displaystyle{ \mathrm{Vect}(S^1) }[/math] consists of smooth vector fields on [math]\displaystyle{ S^1 }[/math].[22] The [math]\displaystyle{ H^1 }[/math] inner product on [math]\displaystyle{ \mathrm{Vect}(S^1) }[/math],

[math]\displaystyle{ \left\langle u \frac{\partial}{\partial x} , v\frac{\partial}{\partial x} \right\rangle_{H^1} = \int_{S^1}(uv+u_xv_x)dx, }[/math]

induces a right-invariant Riemannian metric on [math]\displaystyle{ \mathrm{Diff}(S^1) }[/math]. Here [math]\displaystyle{ x }[/math] is the standard coordinate on [math]\displaystyle{ S^1 }[/math]. Let

[math]\displaystyle{ U(x,t)=u(x,t)\frac{\partial}{\partial x} }[/math]

be a time-dependent vector field on [math]\displaystyle{ S^1 }[/math], and let [math]\displaystyle{ \{\varphi_t\} }[/math] be the flow of [math]\displaystyle{ U }[/math], i.e. the solution to

[math]\displaystyle{ \frac{d}{dt}\varphi_t(x)=u(\varphi_t(x),t). }[/math]

Then [math]\displaystyle{ u }[/math] is a solution to the Camassa–Holm equation with [math]\displaystyle{ \kappa=0 }[/math], if and only if the path [math]\displaystyle{ t\mapsto\varphi_t\in\mathrm{Diff}(S^1) }[/math] is a geodesic on [math]\displaystyle{ \mathrm{Diff}(S^1) }[/math] with respect to the right-invariant [math]\displaystyle{ H^1 }[/math] metric.[23]

For general [math]\displaystyle{ \kappa }[/math], the Camassa–Holm equation corresponds to the geodesic equation of a similar right-invariant metric on the universal central extension of [math]\displaystyle{ \mathrm{Diff}(S^1) }[/math], the Virasoro group.

See also

Notes

  1. ↑ 1.0 1.1 Camassa & Holm 1993.
  2. ↑ Loubet 2005.
  3. ↑ Boldea 1995.
  4. ↑ 4.0 4.1 Constantin & McKean 1999.
  5. ↑ Constantin 2001.
  6. ↑ Constantin, Gerdjikov & Ivanov 2006.
  7. ↑ Drazin & Johnson 1989.
  8. ↑ Beals, Sattinger & Szmigielski 1999.
  9. ↑ Parker 2005.
  10. ↑ 10.0 10.1 Constantin & Strauss 2002.
  11. ↑ Constantin & Strauss 2000.
  12. ↑ Whitham 1974.
  13. ↑ Constantin & Escher 1998.
  14. ↑ Constantin 2000.
  15. ↑ Constantin & Escher 2000.
  16. ↑ McKean 2004.
  17. ↑ Bressan & Constantin 2007a.
  18. ↑ Bressan & Constantin 2007b.
  19. ↑ Boutet de Monvel et al. 2009.
  20. ↑ Eckhardt & Teschl 2013.
  21. ↑ McKean 2003.
  22. ↑ Kriegl & Michor 1997.
  23. ↑ Misiołek 1998.

References

Further reading

Introductions to the subject
Peakon solutions
Water wave theory
Existence, uniqueness, wellposedness, stability, propagation speed, etc.
Travelling waves
Integrability structure (symmetries, hierarchy of soliton equations, conservations laws) and differential-geometric formulation
Others





Retrieved from "https://handwiki.org/wiki/index.php?title=Camassa–Holm_equation&oldid=3381241"