Cellular Potts model

Short description: Computational model of cells and tissues

In computational biology, a Cellular Potts model (CPM, also known as the Glazier-Graner-Hogeweg model) is a computational model of cells and tissues. It is used to simulate individual and collective cell behavior, tissue morphogenesis and cancer development. CPM describes cells as deformable objects with a certain volume, that can adhere to each other and to the medium in which they live. The formalism can be extended to include cell behaviours such as cell migration, growth and division, and cell signalling. The first CPM was proposed for the simulation of cell sorting by François Graner and James Glazier as a modification of a large-Q Potts model. CPM was then popularized by Paulien Hogeweg for studying morphogenesis. Although the model was developed to describe biological cells, it can also be used to model individual parts of a biological cell, or even regions of fluid.

Model description

Cartoon example of lattice used in Cellular Potts Model.

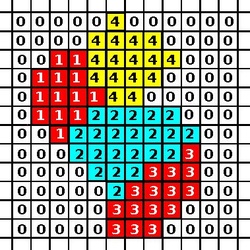
The CPM consists of a rectangular Euclidean lattice, where each cell is a subset of lattice sites sharing the same cell ID (analogous to spin in Potts models in physics). Lattice sites that are not occupied by cells are the medium. The dynamics of the model are governed by an energy function: the Hamiltonian which describes the energy of a particular configuration of cells in the lattice. In a basic CPM, this energy results from adhesion between cells and resistance of cells to volume changes. The algorithm for updating CPM minimizes this energy.

In order to evolve the model Metropolis-style updates are performed, that is:

1. choose a random lattice site i
2. choose a random neighboring lattice site j to copy its ID into i.
3. calculate the difference in energy ([math]\displaystyle{ \Delta H }[/math]) between the original and the proposed new configuration.
4. accept or reject this copy event based on the change in energy [math]\displaystyle{ \Delta H }[/math], as follows:

   if the new energy is lower, always accept the copy;

   if the new energy is higher, accept the copy with probability [math]\displaystyle{ e^{-\Delta H / T} }[/math] (the Boltzmann temperature T determines the likelihood of energetically unfavorable fluctuations).

The Hamiltonian

The original model proposed by Graner and Glazier contains cells of two types, with different adhesion energies for cells of the same type and cells of a different type. Each cell type also has a different contact energy with the medium, and the cell volume is assumed to remain close to a target value. The Hamiltonian is formulated as:

[math]\displaystyle{ \begin{align} H = \sum_{i,j\text{ neighbors}}J\left(\tau(\sigma_i),\tau(\sigma_j)\right)\left(1-\delta(\sigma_i,\sigma_j)\right) + \lambda\sum_{\sigma_i}\left(v(\sigma_i)- V(\sigma_i)\right)^2,\\ \end{align} }[/math]

where i, j are lattice sites, σ_i is the cell at site i, τ(σ) is the cell type of cell σ, J is the coefficient determining the adhesion between two cells of types τ(σ),τ(σ'), δ is the Kronecker delta, v(σ) is the volume of cell σ, V(σ) is the target volume, and λ is a Lagrange multiplier determining the strength of the volume constraint.

Cells with a lower J value for their membrane contact will stick together more strongly. Therefore, different patterns of cell sorting can be simulated by varying the J values.

Extensions

Over time, the CPM has evolved from a specific model of cell sorting to a general framework with many extensions, some of which are partially or entirely off-lattice. Various cell behaviours, such as chemotaxis, elongation and haptotaxis can be incorporated by extending either the Hamiltonian, H, or the change in energy [math]\displaystyle{ \Delta H }[/math]. Auxiliary sub-lattices may be used to include additional spatial information, such as the concentrations of chemicals.

Chemotaxis

In CPM, cells can be made to move in the direction of higher chemokine concentration, by increasing the probability of copying the ID of site j into site i when the chemokine concentration is higher at j. This is done by modifying the change in energy [math]\displaystyle{ \Delta H }[/math] with a term that is proportional to the difference in concentration at i and j:

[math]\displaystyle{ \begin{align} \Delta H'=\Delta H-\mu(C_i-C_j)\\ \end{align} }[/math]

Where [math]\displaystyle{ \mu }[/math] is the strength of chemotactic movement, and [math]\displaystyle{ C_i }[/math] and [math]\displaystyle{ C_j }[/math] are the concentration of the chemokine at site i and j, respectively. The chemokine gradient is typically implemented on a separate lattice of the same dimensions as the cell lattice.

Multiscale and hybrid modeling using CPM

Core GGH (or CPM) algorithm which defines the evolution of the cellular level structures can easily be integrated with intracellular signaling dynamics, reaction diffusion dynamics and rule based model to account for the processes which happen at lower (or higher) time scale. Open source software Bionetsolver can be used to integrate intracellular dynamics with CPM algorithm.

References

• Chen, Nan; Glazier, James A.; Izaguirre, Jesus A.; Alber, Mark S. (2007). "A parallel implementation of the Cellular Potts Model for simulation of cell-based morphogenesis". Computer Physics Communications 176 (11–12): 670–681. doi:10.1016/j.cpc.2007.03.007. PMID 18084624. Bibcode: 2007CoPhC.176..670C. 

External links

• James Glazier (professional website)
• CompuCell3D, a CPM simulation environment: Sourceforge
• SimTK
• Notre Dame development site
• Artificial Life model of multicellular morphogenesis with autonomously generated gradients for positional information using the Cellular Potts model
• Stochastic cellular automata