Euclidean space

Short description: Fundamental space of geometry

A point in three-dimensional Euclidean space can be located by three coordinates.

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension n, which are called Euclidean n-spaces when one wants to specify their dimension. For n equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his Elements, with the great innovation of proving all properties of the space as theorems, by starting from a few fundamental properties, called postulates, which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prove (parallel postulate).

After the introduction at the end of 19th century of non-Euclidean geometries, the old postulates were re-formalized to define Euclidean spaces through axiomatic theory. Another definition of Euclidean spaces by means of vector spaces and linear algebra has been shown to be equivalent to the axiomatic definition. It is this definition that is more commonly used in modern mathematics, and detailed in this article. In all definitions, Euclidean spaces consist of points, which are defined only by the properties that they must have for forming a Euclidean space.

There is essentially only one Euclidean space of each dimension; that is, all Euclidean spaces of a given dimension are isomorphic. Therefore it is usually possible to work with a specific Euclidean space, denoted [math]\displaystyle{ \mathbf{E}^n }[/math] or [math]\displaystyle{ \mathbb{E}^n }[/math], which can be represented using Cartesian coordinates as the real n-space [math]\displaystyle{ \R^n }[/math] equipped with the standard dot product.

Definition

History of the definition

Euclidean space was introduced by ancient Greeks as an abstraction of our physical space. Their great innovation, appearing in Euclid's Elements was to build and prove all geometry by starting from a few very basic properties, which are abstracted from the physical world, and cannot be mathematically proved because of the lack of more basic tools. These properties are called postulates, or axioms in modern language. This way of defining Euclidean space is still in use under the name of synthetic geometry.

In 1637, René Descartes introduced Cartesian coordinates, and showed that these allow reducing geometric problems to algebraic computations with numbers. This reduction of geometry to algebra was a major change in point of view, as, until then, the real numbers were defined in terms of lengths and distances.

Euclidean geometry was not applied in spaces of dimension more than three until the 19th century. Ludwig Schläfli generalized Euclidean geometry to spaces of dimension n, using both synthetic and algebraic methods, and discovered all of the regular polytopes (higher-dimensional analogues of the Platonic solids) that exist in Euclidean spaces of any dimension.

Despite the wide use of Descartes' approach, which was called analytic geometry, the definition of Euclidean space remained unchanged until the end of 19th century. The introduction of abstract vector spaces allowed their use in defining Euclidean spaces with a purely algebraic definition. This new definition has been shown to be equivalent to the classical definition in terms of geometric axioms. It is this algebraic definition that is now most often used for introducing Euclidean spaces.

Motivation of the modern definition

One way to think of the Euclidean plane is as a set of points satisfying certain relationships, expressible in terms of distance and angles. For example, there are two fundamental operations (referred to as motions) on the plane. One is translation, which means a shifting of the plane so that every point is shifted in the same direction and by the same distance. The other is rotation around a fixed point in the plane, in which all points in the plane turn around that fixed point through the same angle. One of the basic tenets of Euclidean geometry is that two figures (usually considered as subsets) of the plane should be considered equivalent (congruent) if one can be transformed into the other by some sequence of translations, rotations and reflections (see below).

In order to make all of this mathematically precise, the theory must clearly define what is a Euclidean space, and the related notions of distance, angle, translation, and rotation. Even when used in physical theories, Euclidean space is an abstraction detached from actual physical locations, specific reference frames, measurement instruments, and so on. A purely mathematical definition of Euclidean space also ignores questions of units of length and other physical dimensions: the distance in a "mathematical" space is a number, not something expressed in inches or metres.

The standard way to mathematically define a Euclidean space, as carried out in the remainder of this article, is as a set of points on which a real vector space acts — the space of translations which is equipped with an inner product. The action of translations makes the space an affine space, and this allows defining lines, planes, subspaces, dimension, and parallelism. The inner product allows defining distance and angles.

The set [math]\displaystyle{ \R^n }[/math] of n-tuples of real numbers equipped with the dot product is a Euclidean space of dimension n. Conversely, the choice of a point called the origin and an orthonormal basis of the space of translations is equivalent with defining an isomorphism between a Euclidean space of dimension n and [math]\displaystyle{ \R^n }[/math] viewed as a Euclidean space.

It follows that everything that can be said about a Euclidean space can also be said about [math]\displaystyle{ \R^n. }[/math] Therefore, many authors, especially at elementary level, call [math]\displaystyle{ \R^n }[/math] the standard Euclidean space of dimension n, or simply the Euclidean space of dimension n.

A reason for introducing such an abstract definition of Euclidean spaces, and for working with it instead of [math]\displaystyle{ \R^n }[/math] is that it is often preferable to work in a coordinate-free and origin-free manner (that is, without choosing a preferred basis and a preferred origin). Another reason is that there is no origin nor any basis in the physical world.

Technical definition

A Euclidean vector space is a finite-dimensional inner product space over the real numbers.

A Euclidean space is an affine space over the reals such that the associated vector space is a Euclidean vector space. Euclidean spaces are sometimes called Euclidean affine spaces to distinguish them from Euclidean vector spaces.

If E is a Euclidean space, its associated vector space (Euclidean vector space) is often denoted [math]\displaystyle{ \overrightarrow E. }[/math] The dimension of a Euclidean space is the dimension of its associated vector space.

The elements of E are called points, and are commonly denoted by capital letters. The elements of [math]\displaystyle{ \overrightarrow E }[/math] are called Euclidean vectors or free vectors. They are also called translations, although, properly speaking, a translation is the geometric transformation resulting from the action of a Euclidean vector on the Euclidean space.

The action of a translation v on a point P provides a point that is denoted P + v. This action satisfies

[math]\displaystyle{ P+(v+w)= (P+v)+w. }[/math]

Note: The second + in the left-hand side is a vector addition; each other + denotes an action of a vector on a point. This notation is not ambiguous, as, to distinguish between the two meanings of +, it suffices to look at the nature of its left argument.

The fact that the action is free and transitive means that, for every pair of points (P, Q), there is exactly one displacement vector v such that P + v = Q. This vector v is denoted Q − P or [math]\displaystyle{ \overrightarrow {PQ}\vphantom{\frac){}}. }[/math]

As previously explained, some of the basic properties of Euclidean spaces result from the structure of affine space. They are described in § Affine structure and its subsections. The properties resulting from the inner product are explained in § Metric structure and its subsections.

Prototypical examples

For any vector space, the addition acts freely and transitively on the vector space itself. Thus a Euclidean vector space can be viewed as a Euclidean space that has itself as the associated vector space.

A typical case of Euclidean vector space is [math]\displaystyle{ \R^n }[/math] viewed as a vector space equipped with the dot product as an inner product. The importance of this particular example of Euclidean space lies in the fact that every Euclidean space is isomorphic to it. More precisely, given a Euclidean space E of dimension n, the choice of a point, called an origin and an orthonormal basis of [math]\displaystyle{ \overrightarrow E }[/math] defines an isomorphism of Euclidean spaces from E to [math]\displaystyle{ \R^n. }[/math]

As every Euclidean space of dimension n is isomorphic to it, the Euclidean space [math]\displaystyle{ \R^n }[/math] is sometimes called the standard Euclidean space of dimension n.

Affine structure

Some basic properties of Euclidean spaces depend only on the fact that a Euclidean space is an affine space. They are called affine properties and include the concepts of lines, subspaces, and parallelism, which are detailed in next subsections.

Subspaces

Let E be a Euclidean space and [math]\displaystyle{ \overrightarrow E }[/math] its associated vector space.

A flat, Euclidean subspace or affine subspace of E is a subset F of E such that

[math]\displaystyle{ \overrightarrow F = \Bigl\{\overrightarrow {PQ} \mathrel{\Big|} P\in F, Q\in F \Bigr\}\vphantom{\frac({}} }[/math]

as the associated vector space of F is a linear subspace (vector subspace) of [math]\displaystyle{ \overrightarrow E. }[/math] A Euclidean subspace F is a Euclidean space with [math]\displaystyle{ \overrightarrow F }[/math] as the associated vector space. This linear subspace [math]\displaystyle{ \overrightarrow F }[/math] is also called the direction of F.

If P is a point of F then

[math]\displaystyle{ F = \Bigl\{P+v \mathrel{\Big|} v\in \overrightarrow F \Bigr\}. }[/math]

Conversely, if P is a point of E and [math]\displaystyle{ \overrightarrow V }[/math] is a linear subspace of [math]\displaystyle{ \overrightarrow E, }[/math] then

[math]\displaystyle{ P + \overrightarrow V = \Bigl\{P + v \mathrel{\Big|} v\in \overrightarrow V \Bigr\} }[/math]

is a Euclidean subspace of direction [math]\displaystyle{ \overrightarrow V }[/math]. (The associated vector space of this subspace is [math]\displaystyle{ \overrightarrow V }[/math].)

A Euclidean vector space [math]\displaystyle{ \overrightarrow E }[/math] (that is, a Euclidean space that is equal to [math]\displaystyle{ \overrightarrow E }[/math]) has two sorts of subspaces: its Euclidean subspaces and its linear subspaces. Linear subspaces are Euclidean subspaces and a Euclidean subspace is a linear subspace if and only if it contains the zero vector.

Lines and segments

In a Euclidean space, a line is a Euclidean subspace of dimension one. Since a vector space of dimension one is spanned by any nonzero vector, a line is a set of the form

[math]\displaystyle{ \Bigl\{P + \lambda \overrightarrow{PQ} \mathrel{\Big|} \lambda \in \R \Bigr\},\vphantom{\frac({}} }[/math]

where P and Q are two distinct points of the Euclidean space as a part of the line.

It follows that there is exactly one line that passes through (contains) two distinct points. This implies that two distinct lines intersect in at most one point.

A more symmetric representation of the line passing through P and Q is

[math]\displaystyle{ \Bigl\{O + (1-\lambda)\overrightarrow{OP} + \lambda \overrightarrow{OQ} \mathrel{\Big|} \lambda \in \R \Bigr\},\vphantom{\frac({}} }[/math]

where O is an arbitrary point (not necessary on the line).

In a Euclidean vector space, the zero vector is usually chosen for O; this allows simplifying the preceding formula into

[math]\displaystyle{ \bigl\{(1-\lambda) P + \lambda Q \mathrel{\big|} \lambda \in \R\bigr\}. }[/math]

A standard convention allows using this formula in every Euclidean space, see Affine space § Affine combinations and barycenter.

The line segment, or simply segment, joining the points P and Q is the subset of points such that 0 ≤ 𝜆 ≤ 1 in the preceding formulas. It is denoted PQ or QP; that is

[math]\displaystyle{ PQ = QP = \Bigl\{P+\lambda \overrightarrow{PQ} \mathrel{\Big|} 0 \le \lambda \le 1\Bigr\}.\vphantom{\frac({}} }[/math]

Parallelism

Two subspaces S and T of the same dimension in a Euclidean space are parallel if they have the same direction (i.e., the same associated vector space). Equivalently, they are parallel, if there is a translation vector v that maps one to the other:

[math]\displaystyle{ T= S+v. }[/math]

Given a point P and a subspace S, there exists exactly one subspace that contains P and is parallel to S, which is [math]\displaystyle{ P + \overrightarrow S. }[/math] In the case where S is a line (subspace of dimension one), this property is Playfair's axiom.

It follows that in a Euclidean plane, two lines either meet in one point or are parallel.

The concept of parallel subspaces has been extended to subspaces of different dimensions: two subspaces are parallel if the direction of one of them is contained in the direction to the other.

Metric structure

The vector space [math]\displaystyle{ \overrightarrow E }[/math] associated to a Euclidean space E is an inner product space. This implies a symmetric bilinear form

[math]\displaystyle{ \begin{align} \overrightarrow E \times \overrightarrow E &\to \R\\ (x,y)&\mapsto \langle x,y \rangle \end{align} }[/math]

that is positive definite (that is [math]\displaystyle{ \langle x,x \rangle }[/math] is always positive for x ≠ 0).

The inner product of a Euclidean space is often called dot product and denoted x ⋅ y. This is specially the case when a Cartesian coordinate system has been chosen, as, in this case, the inner product of two vectors is the dot product of their coordinate vectors. For this reason, and for historical reasons, the dot notation is more commonly used than the bracket notation for the inner product of Euclidean spaces. This article will follow this usage; that is [math]\displaystyle{ \langle x,y \rangle }[/math] will be denoted x ⋅ y in the remainder of this article.

The Euclidean norm of a vector x is

[math]\displaystyle{ \|x\| = \sqrt {x \cdot x}. }[/math]

The inner product and the norm allows expressing and proving metric and topological properties of Euclidean geometry. The next subsection describe the most fundamental ones. In these subsections, E denotes an arbitrary Euclidean space, and [math]\displaystyle{ \overrightarrow E }[/math] denotes its vector space of translations.

Distance and length

The distance (more precisely the Euclidean distance) between two points of a Euclidean space is the norm of the translation vector that maps one point to the other; that is

[math]\displaystyle{ d(P,Q) = \Bigl\|\overrightarrow {PQ}\Bigr\|.\vphantom{\frac({}} }[/math]

The length of a segment PQ is the distance d(P, Q) between its endpoints P and Q. It is often denoted [math]\displaystyle{ |PQ| }[/math].

The distance is a metric, as it is positive definite, symmetric, and satisfies the triangle inequality

[math]\displaystyle{ d(P,Q)\le d(P,R) + d(R, Q). }[/math]

Moreover, the equality is true if and only if a point R belongs to the segment PQ. This inequality means that the length of any edge of a triangle is smaller than the sum of the lengths of the other edges. This is the origin of the term triangle inequality.

With the Euclidean distance, every Euclidean space is a complete metric space.

Orthogonality

Two nonzero vectors u and v of [math]\displaystyle{ \overrightarrow E }[/math] (the associated vector space of a Euclidean space E) are perpendicular or orthogonal if their inner product is zero:

[math]\displaystyle{ u \cdot v =0 }[/math]

Two linear subspaces of [math]\displaystyle{ \overrightarrow E }[/math] are orthogonal if every nonzero vector of the first one is perpendicular to every nonzero vector of the second one. This implies that the intersection of the linear subspaces is reduced to the zero vector.

Two lines, and more generally two Euclidean subspaces (A line can be considered as one Euclidean subspace.) are orthogonal if their directions (the associated vector spaces of the Euclidean subspaces) are orthogonal. Two orthogonal lines that intersect are said perpendicular.

Two segments AB and AC that share a common endpoint A are perpendicular or form a right angle if the vectors [math]\displaystyle{ \overrightarrow {AB}\vphantom{\frac){}} }[/math] and [math]\displaystyle{ \overrightarrow {AC}\vphantom{\frac){}} }[/math] are orthogonal.

If AB and AC form a right angle, one has

[math]\displaystyle{ |BC|^2 = |AB|^2 + |AC|^2. }[/math]

This is the Pythagorean theorem. Its proof is easy in this context, as, expressing this in terms of the inner product, one has, using bilinearity and symmetry of the inner product:

[math]\displaystyle{ \begin{align} |BC|^2 &= \overrightarrow {BC}\cdot \overrightarrow {BC} \vphantom{\frac({}}\\[2mu] &=\Bigl(\overrightarrow {BA}+\overrightarrow {AC}\Bigr) \cdot \Bigl(\overrightarrow {BA}+\overrightarrow {AC}\Bigr)\\[4mu] &=\overrightarrow {BA}\cdot \overrightarrow {BA}+ \overrightarrow {AC}\cdot \overrightarrow {AC} -2 \overrightarrow {AB}\cdot \overrightarrow {AC}\\[6mu] &=\overrightarrow {AB}\cdot \overrightarrow {AB} + \overrightarrow {AC}\cdot\overrightarrow {AC}\\[6mu] &=|AB|^2 + |AC|^2. \end{align} }[/math]

Here, [math]\displaystyle{ \overrightarrow {AB}\cdot \overrightarrow {AC} = 0 \vphantom{\frac({}} }[/math] is used since these two vectors are orthogonal.

Angle

Positive and negative angles on the oriented plane

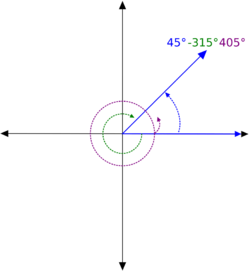
The (non-oriented) angle θ between two nonzero vectors x and y in [math]\displaystyle{ \overrightarrow E }[/math] is

[math]\displaystyle{ \theta = \arccos\left(\frac{x\cdot y}{|x|\,|y|}\right) }[/math]

where arccos is the principal value of the arccosine function. By Cauchy–Schwarz inequality, the argument of the arccosine is in the interval [−1, 1]. Therefore θ is real, and 0 ≤ θ ≤ π (or 0 ≤ θ ≤ 180 if angles are measured in degrees).

Angles are not useful in a Euclidean line, as they can be only 0 or π.

In an oriented Euclidean plane, one can define the oriented angle of two vectors. The oriented angle of two vectors x and y is then the opposite of the oriented angle of y and x. In this case, the angle of two vectors can have any value modulo an integer multiple of 2π. In particular, a reflex angle π < θ < 2π equals the negative angle −π < θ − 2π < 0.

The angle of two vectors does not change if they are multiplied by positive numbers. More precisely, if x and y are two vectors, and λ and μ are real numbers, then

[math]\displaystyle{ \operatorname{angle}(\lambda x, \mu y)= \begin{cases} \operatorname{angle}(x, y) \qquad\qquad \text{if } \lambda \text{ and } \mu \text{ have the same sign}\\ \pi - \operatorname{angle}(x, y)\qquad \text{otherwise}. \end{cases} }[/math]

If A, B, and C are three points in a Euclidean space, the angle of the segments AB and AC is the angle of the vectors [math]\displaystyle{ \overrightarrow {AB}\vphantom{\frac({}} }[/math] and [math]\displaystyle{ \overrightarrow {AC}.\vphantom{\frac({}} }[/math] As the multiplication of vectors by positive numbers do not change the angle, the angle of two half-lines with initial point A can be defined: it is the angle of the segments AB and AC, where B and C are arbitrary points, one on each half-line. Although this is less used, one can define similarly the angle of segments or half-lines that do not share an initial point.

The angle of two lines is defined as follows. If θ is the angle of two segments, one on each line, the angle of any two other segments, one on each line, is either θ or π − θ. One of these angles is in the interval [0, π/2], and the other being in [π/2, π]. The non-oriented angle of the two lines is the one in the interval [0, π/2]. In an oriented Euclidean plane, the oriented angle of two lines belongs to the interval [−π/2, π/2].

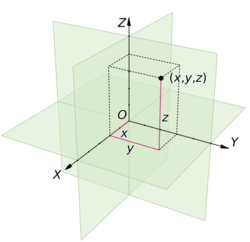
Cartesian coordinates

Every Euclidean vector space has an orthonormal basis (in fact, infinitely many in dimension higher than one, and two in dimension one), that is a basis [math]\displaystyle{ (e_1, \dots, e_n) }[/math] of unit vectors ([math]\displaystyle{ \|e_i\| = 1 }[/math]) that are pairwise orthogonal ([math]\displaystyle{ e_i\cdot e_j = 0 }[/math] for i ≠ j). More precisely, given any basis [math]\displaystyle{ (b_1, \dots, b_n), }[/math] the Gram–Schmidt process computes an orthonormal basis such that, for every i, the linear spans of [math]\displaystyle{ (e_1, \dots, e_i) }[/math] and [math]\displaystyle{ (b_1, \dots, b_i) }[/math] are equal.

Given a Euclidean space E, a Cartesian frame is a set of data consisting of an orthonormal basis of [math]\displaystyle{ \overrightarrow E, }[/math] and a point of E, called the origin and often denoted O. A Cartesian frame [math]\displaystyle{ (O, e_1, \dots, e_n) }[/math] allows defining Cartesian coordinates for both E and [math]\displaystyle{ \overrightarrow E }[/math] in the following way.

The Cartesian coordinates of a vector v of [math]\displaystyle{ \overrightarrow E }[/math] are the coefficients of v on the orthonormal basis [math]\displaystyle{ e_1, \dots, e_n. }[/math] For example, the Cartesian coordinates of a vector [math]\displaystyle{ v }[/math] on an orthonormal basis [math]\displaystyle{ (e_1,e_2,e_3) }[/math] (that may be named as [math]\displaystyle{ (x,y,z) }[/math] as a convention) in a 3-dimensional Euclidean space is [math]\displaystyle{ (\alpha_1,\alpha_2,\alpha_3) }[/math] if [math]\displaystyle{ v = \alpha_1 e_1 + \alpha_2 e_2 + \alpha_3 e_3 }[/math]. As the basis is orthonormal, the i-th coefficient [math]\displaystyle{ \alpha_i }[/math] is equal to the dot product [math]\displaystyle{ v\cdot e_i. }[/math]

The Cartesian coordinates of a point P of E are the Cartesian coordinates of the vector [math]\displaystyle{ \overrightarrow {OP}.\vphantom{\frac({}} }[/math]

Other coordinates

3-dimensional skew coordinates

As a Euclidean space is an affine space, one can consider an affine frame on it, which is the same as a Euclidean frame, except that the basis is not required to be orthonormal. This define affine coordinates, sometimes called skew coordinates for emphasizing that the basis vectors are not pairwise orthogonal.

An affine basis of a Euclidean space of dimension n is a set of n + 1 points that are not contained in a hyperplane. An affine basis define barycentric coordinates for every point.

Many other coordinates systems can be defined on a Euclidean space E of dimension n, in the following way. Let f be a homeomorphism (or, more often, a diffeomorphism) from a dense open subset of E to an open subset of [math]\displaystyle{ \R^n. }[/math] The coordinates of a point x of E are the components of f(x). The polar coordinate system (dimension 2) and the spherical and cylindrical coordinate systems (dimension 3) are defined this way.

For points that are outside the domain of f, coordinates may sometimes be defined as the limit of coordinates of neighbour points, but these coordinates may be not uniquely defined, and may be not continuous in the neighborhood of the point. For example, for the spherical coordinate system, the longitude is not defined at the pole, and on the antimeridian, the longitude passes discontinuously from –180° to +180°.

This way of defining coordinates extends easily to other mathematical structures, and in particular to manifolds.

Isometries

An isometry between two metric spaces is a bijection preserving the distance, that is

[math]\displaystyle{ d(f(x), f(y))= d(x,y). }[/math]

In the case of a Euclidean vector space, an isometry that maps the origin to the origin preserves the norm

[math]\displaystyle{ \|f(x)\| = \|x\|, }[/math]

since the norm of a vector is its distance from the zero vector. It preserves also the inner product

[math]\displaystyle{ f(x)\cdot f(y)=x\cdot y, }[/math]

since

[math]\displaystyle{ x \cdot y=\tfrac 1 2 \left(\|x+y\|^2 - \|x\|^2 - \|y\|^2\right). }[/math]

An isometry of Euclidean vector spaces is a linear isomorphism.

An isometry [math]\displaystyle{ f\colon E\to F }[/math] of Euclidean spaces defines an isometry [math]\displaystyle{ \overrightarrow f \colon \overrightarrow E \to \overrightarrow F }[/math] of the associated Euclidean vector spaces. This implies that two isometric Euclidean spaces have the same dimension. Conversely, if E and F are Euclidean spaces, O ∈ E, O′ ∈ F, and [math]\displaystyle{ \overrightarrow f\colon \overrightarrow E\to \overrightarrow F }[/math] is an isometry, then the map [math]\displaystyle{ f\colon E\to F }[/math] defined by

[math]\displaystyle{ f(P)=O' + \overrightarrow f\Bigl(\overrightarrow{OP}\Bigr)\vphantom{\frac({}} }[/math]

is an isometry of Euclidean spaces.

It follows from the preceding results that an isometry of Euclidean spaces maps lines to lines, and, more generally Euclidean subspaces to Euclidean subspaces of the same dimension, and that the restriction of the isometry on these subspaces are isometries of these subspaces.

Isometry with prototypical examples

If E is a Euclidean space, its associated vector space [math]\displaystyle{ \overrightarrow E }[/math] can be considered as a Euclidean space. Every point O ∈ E defines an isometry of Euclidean spaces

[math]\displaystyle{ P\mapsto \overrightarrow {OP},\vphantom{\frac({}} }[/math]

which maps O to the zero vector and has the identity as associated linear map. The inverse isometry is the map

[math]\displaystyle{ v\mapsto O+v. }[/math]

A Euclidean frame [math]\displaystyle{ (O, e_1, \dots, e_n) }[/math] allows defining the map

[math]\displaystyle{ \begin{align} E&\to \R^n\\ P&\mapsto \Bigl(e_1\cdot \overrightarrow {OP}, \dots, e_n\cdot\overrightarrow {OP}\Bigr),\vphantom{\frac({}} \end{align} }[/math]

which is an isometry of Euclidean spaces. The inverse isometry is

[math]\displaystyle{ \begin{align} \R^n&\to E \\ (x_1\dots, x_n)&\mapsto \left(O+x_1e_1+ \dots + x_ne_n\right). \end{align} }[/math]

This means that, up to an isomorphism, there is exactly one Euclidean space of a given dimension.

This justifies that many authors talk of [math]\displaystyle{ \R^n }[/math] as the Euclidean space of dimension n.

Euclidean group

An isometry from a Euclidean space onto itself is called Euclidean isometry, Euclidean transformation or rigid transformation. The rigid transformations of a Euclidean space form a group (under composition), called the Euclidean group and often denoted E(n) of ISO(n).

The simplest Euclidean transformations are translations

[math]\displaystyle{ P \to P+v. }[/math]

They are in bijective correspondence with vectors. This is a reason for calling space of translations the vector space associated to a Euclidean space. The translations form a normal subgroup of the Euclidean group.

A Euclidean isometry f of a Euclidean space E defines a linear isometry [math]\displaystyle{ \overrightarrow f }[/math] of the associated vector space (by linear isometry, it is meant an isometry that is also a linear map) in the following way: denoting by Q – P the vector [math]\displaystyle{ \overrightarrow {PQ},\vphantom{\frac({}} }[/math] if O is an arbitrary point of E, one has

[math]\displaystyle{ \overrightarrow f\Bigl(\overrightarrow {OP}\Bigr)= f(P)-f(O).\vphantom{\frac({}} }[/math]

It is straightforward to prove that this is a linear map that does not depend from the choice of O.

The map [math]\displaystyle{ f \to \overrightarrow f }[/math] is a group homomorphism from the Euclidean group onto the group of linear isometries, called the orthogonal group. The kernel of this homomorphism is the translation group, showing that it is a normal subgroup of the Euclidean group.

The isometries that fix a given point P form the stabilizer subgroup of the Euclidean group with respect to P. The restriction to this stabilizer of above group homomorphism is an isomorphism. So the isometries that fix a given point form a group isomorphic to the orthogonal group.

Let P be a point, f an isometry, and t the translation that maps P to f(P). The isometry [math]\displaystyle{ g=t^{-1}\circ f }[/math] fixes P. So [math]\displaystyle{ f= t\circ g, }[/math] and the Euclidean group is the semidirect product of the translation group and the orthogonal group.

The special orthogonal group is the normal subgroup of the orthogonal group that preserves handedness. It is a subgroup of index two of the orthogonal group. Its inverse image by the group homomorphism [math]\displaystyle{ f \to \overrightarrow f }[/math] is a normal subgroup of index two of the Euclidean group, which is called the special Euclidean group or the displacement group. Its elements are called rigid motions or displacements.

Rigid motions include the identity, translations, rotations (the rigid motions that fix at least a point), and also screw motions.

Typical examples of rigid transformations that are not rigid motions are reflections, which are rigid transformations that fix a hyperplane and are not the identity. They are also the transformations consisting in changing the sign of one coordinate over some Euclidean frame.

As the special Euclidean group is a subgroup of index two of the Euclidean group, given a reflection r, every rigid transformation that is not a rigid motion is the product of r and a rigid motion. A glide reflection is an example of a rigid transformation that is not a rigid motion or a reflection.

All groups that have been considered in this section are Lie groups and algebraic groups.

Topology

The Euclidean distance makes a Euclidean space a metric space, and thus a topological space. This topology is called the Euclidean topology. In the case of [math]\displaystyle{ \mathbb R^n, }[/math] this topology is also the product topology.

The open sets are the subsets that contains an open ball around each of their points. In other words, open balls form a base of the topology.

The topological dimension of a Euclidean space equals its dimension. This implies that Euclidean spaces of different dimensions are not homeomorphic. Moreover, the theorem of invariance of domain asserts that a subset of a Euclidean space is open (for the subspace topology) if and only if it is homeomorphic to an open subset of a Euclidean space of the same dimension.

Euclidean spaces are complete and locally compact. That is, a closed subset of a Euclidean space is compact if it is bounded (that is, contained in a ball). In particular, closed balls are compact.

Axiomatic definitions

The definition of Euclidean spaces that has been described in this article differs fundamentally of Euclid's one. In reality, Euclid did not define formally the space, because it was thought as a description of the physical world that exists independently of human mind. The need of a formal definition appeared only at the end of 19th century, with the introduction of non-Euclidean geometries.

Two different approaches have been used. Felix Klein suggested to define geometries through their symmetries. The presentation of Euclidean spaces given in this article, is essentially issued from his Erlangen program, with the emphasis given on the groups of translations and isometries.

On the other hand, David Hilbert proposed a set of axioms, inspired by Euclid's postulates. They belong to synthetic geometry, as they do not involve any definition of real numbers. Later G. D. Birkhoff and Alfred Tarski proposed simpler sets of axioms, which use real numbers (see Birkhoff's axioms and Tarski's axioms).

In Geometric Algebra, Emil Artin has proved that all these definitions of a Euclidean space are equivalent. It is rather easy to prove that all definitions of Euclidean spaces satisfy Hilbert's axioms, and that those involving real numbers (including the above given definition) are equivalent. The difficult part of Artin's proof is the following. In Hilbert's axioms, congruence is an equivalence relation on segments. One can thus define the length of a segment as its equivalence class. One must thus prove that this length satisfies properties that characterize nonnegative real numbers. Artin proved this with axioms equivalent to those of Hilbert.

Usage

Since ancient Greeks, Euclidean space is used for modeling shapes in the physical world. It is thus used in many sciences such as physics, mechanics, and astronomy. It is also widely used in all technical areas that are concerned with shapes, figure, location and position, such as architecture, geodesy, topography, navigation, industrial design, or technical drawing.

Space of dimensions higher than three occurs in several modern theories of physics; see Higher dimension. They occur also in configuration spaces of physical systems.

Beside Euclidean geometry, Euclidean spaces are also widely used in other areas of mathematics. Tangent spaces of differentiable manifolds are Euclidean vector spaces. More generally, a manifold is a space that is locally approximated by Euclidean spaces. Most non-Euclidean geometries can be modeled by a manifold, and embedded in a Euclidean space of higher dimension. For example, an elliptic space can be modeled by an ellipsoid. It is common to represent in a Euclidean space mathematical objects that are a priori not of a geometrical nature. An example among many is the usual representation of graphs.

Other geometric spaces

Since the introduction, at the end of 19th century, of non-Euclidean geometries, many sorts of spaces have been considered, about which one can do geometric reasoning in the same way as with Euclidean spaces. In general, they share some properties with Euclidean spaces, but may also have properties that could appear as rather strange. Some of these spaces use Euclidean geometry for their definition, or can be modeled as subspaces of a Euclidean space of higher dimension. When such a space is defined by geometrical axioms, embedding the space in a Euclidean space is a standard way for proving consistency of its definition, or, more precisely for proving that its theory is consistent, if Euclidean geometry is consistent (which cannot be proved).

Affine space

A Euclidean space is an affine space equipped with a metric. Affine spaces have many other uses in mathematics. In particular, as they are defined over any field, they allow doing geometry in other contexts.

As soon as non-linear questions are considered, it is generally useful to consider affine spaces over the complex numbers as an extension of Euclidean spaces. For example, a circle and a line have always two intersection points (possibly not distinct) in the complex affine space. Therefore, most of algebraic geometry is built in complex affine spaces and affine spaces over algebraically closed fields. The shapes that are studied in algebraic geometry in these affine spaces are therefore called affine algebraic varieties.

Affine spaces over the rational numbers and more generally over algebraic number fields provide a link between (algebraic) geometry and number theory. For example, the Fermat's Last Theorem can be stated "a Fermat curve of degree higher than two has no point in the affine plane over the rationals."

Geometry in affine spaces over a finite fields has also been widely studied. For example, elliptic curves over finite fields are widely used in cryptography.

Projective space

Originally, projective spaces have been introduced by adding "points at infinity" to Euclidean spaces, and, more generally to affine spaces, in order to make true the assertion "two coplanar lines meet in exactly one point". Projective space share with Euclidean and affine spaces the property of being isotropic, that is, there is no property of the space that allows distinguishing between two points or two lines. Therefore, a more isotropic definition is commonly used, which consists as defining a projective space as the set of the vector lines in a vector space of dimension one more.

As for affine spaces, projective spaces are defined over any field, and are fundamental spaces of algebraic geometry.

Non-Euclidean geometries

Non-Euclidean geometry refers usually to geometrical spaces where the parallel postulate is false. They include elliptic geometry, where the sum of the angles of a triangle is more than 180°, and hyperbolic geometry, where this sum is less than 180°. Their introduction in the second half of 19th century, and the proof that their theory is consistent (if Euclidean geometry is not contradictory) is one of the paradoxes that are at the origin of the foundational crisis in mathematics of the beginning of 20th century, and motivated the systematization of axiomatic theories in mathematics.

Curved spaces

Further information: Manifold and Riemannian manifold

A manifold is a space that in the neighborhood of each point resembles a Euclidean space. In technical terms, a manifold is a topological space, such that each point has a neighborhood that is homeomorphic to an open subset of a Euclidean space. Manifolds can be classified by increasing degree of this "resemblance" into topological manifolds, differentiable manifolds, smooth manifolds, and analytic manifolds. However, none of these types of "resemblance" respect distances and angles, even approximately.

Distances and angles can be defined on a smooth manifold by providing a smoothly varying Euclidean metric on the tangent spaces at the points of the manifold (these tangent spaces are thus Euclidean vector spaces). This results in a Riemannian manifold. Generally, straight lines do not exist in a Riemannian manifold, but their role is played by geodesics, which are the "shortest paths" between two points. This allows defining distances, which are measured along geodesics, and angles between geodesics, which are the angle of their tangents in the tangent space at their intersection. So, Riemannian manifolds behave locally like a Euclidean space that has been bent.

Euclidean spaces are trivially Riemannian manifolds. An example illustrating this well is the surface of a sphere. In this case, geodesics are arcs of great circle, which are called orthodromes in the context of navigation. More generally, the spaces of non-Euclidean geometries can be realized as Riemannian manifolds.

Pseudo-Euclidean space

An inner product of a real vector space is a positive definite bilinear form, and so characterized by a positive definite quadratic form. A pseudo-Euclidean space is an affine space with an associated real vector space equipped with a non-degenerate quadratic form (that may be indefinite).

A fundamental example of such a space is the Minkowski space, which is the space-time of Einstein's special relativity. It is a four-dimensional space, where the metric is defined by the quadratic form

[math]\displaystyle{ x^2+y^2+z^2-t^2, }[/math]

where the last coordinate (t) is temporal, and the other three (x, y, z) are spatial.

To take gravity into account, general relativity uses a pseudo-Riemannian manifold that has Minkowski spaces as tangent spaces. The curvature of this manifold at a point is a function of the value of the gravitational field at this point.

See also

• Hilbert space, a generalization to infinite dimension, used in functional analysis
• Position space, an application in physics

References

• Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: John Wiley & Sons, ISBN 0-471-84819-0 
• Artin, Emil (1988), Geometric Algebra, Wiley Classics Library, New York: John Wiley & Sons Inc., pp. x+214, doi:10.1002/9781118164518, ISBN 0-471-60839-4 
• Ball, W.W. Rouse (1960). A Short Account of the History of Mathematics (4th ed.). Dover Publications. ISBN 0-486-20630-0. https://archive.org/details/shortaccountofhi0000ball. 
• Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3 
• Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover. ""Schläfli ... discovered them before 1853 -- a time when Cayley, Grassman and Möbius were the only other people who had ever conceived of the possibility of geometry in more than three dimensions."" 
• Hazewinkel, Michiel, ed. (2001), "Euclidean space", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/e036380