Chebyshev rational functions
From HandWiki
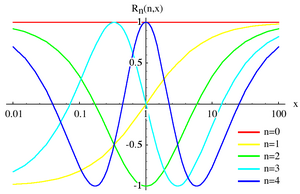
In mathematics, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal. They are named after Pafnuty Chebyshev. A rational Chebyshev function of degree n is defined as:
where Tn(x) is a Chebyshev polynomial of the first kind.
Properties
Many properties can be derived from the properties of the Chebyshev polynomials of the first kind. Other properties are unique to the functions themselves.
Recursion
Differential equations
Orthogonality
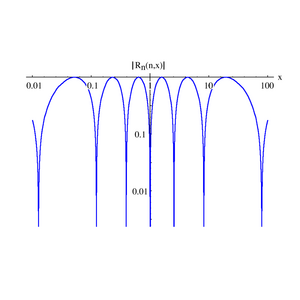
Defining:
The orthogonality of the Chebyshev rational functions may be written:
where cn = 2 for n = 0 and cn = 1 for n ≥ 1; δnm is the Kronecker delta function.
Expansion of an arbitrary function
For an arbitrary function f(x) ∈ L2ω the orthogonality relationship can be used to expand f(x):
where
Particular values
Partial fraction expansion
References
- Guo, Ben-Yu; Shen, Jie; Wang, Zhong-Qing (2002). "Chebyshev rational spectral and pseudospectral methods on a semi-infinite interval". Int. J. Numer. Methods Eng. 53 (1): 65–84. doi:10.1002/nme.392. Bibcode: 2002IJNME..53...65G. http://www.math.purdue.edu/~shen/pub/GSW_IJNME02.pdf. Retrieved 2006-07-25.
 |
