Circular section

tri-axial ellipsoid with a circular section

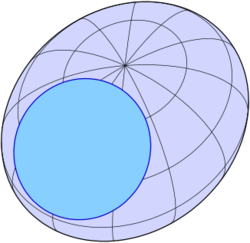
In geometry, a circular section is a circle on a quadric surface (such as an ellipsoid or hyperboloid). It is a special plane section of the quadric, as this circle is the intersection with the quadric of the plane containing the circle.

Any plane section of a sphere is a circular section, if it contains at least 2 points. Any quadric of revolution contains circles as sections with planes that are orthogonal to its axis; it does not contain any other circles, if it is not a sphere. More hidden are circles on other quadrics, such as tri-axial ellipsoids, elliptic cylinders, etc. Nevertheless, it is true that:

• Any quadric surface which contains ellipses contains circles, too.

Equivalently, all quadric surfaces contain circles except parabolic and hyperbolic cylinders and hyperbolic paraboloids.

If a quadric contains a circle, then every intersection of the quadric with a plane parallel to this circle is also a circle, provided it contains at least two points. Except for spheres, the circles contained in a quadric, if any, are all parallel to one of two fixed planes (which are equal in the case of a quadric of revolution).

Circular sections are used in crystallography.

Using projective geometry

The circular sections of a quadric may be computed from the implicit equation of the quadric, as it is done in the following sections. They may also be characterised and studied by using synthetic projective geometry.

Let C be the intersection of a quadric surface Q and a plane P. In this section, Q and C are surfaces in the three-dimensional Euclidean space, which are extended to the projective space over the complex numbers. Under these hypotheses, the curve C is a circle if and only if its intersection with the plane at infinity is included in the ombilic (the curve at infinity of equation [math]\displaystyle{ x^2+y^2+z^2=0 }[/math]).

The first case to be considered is when the intersection of Q with the plane at infinity consists of one or two real lines, that is when Q is either a hyperbolic paraboloid, a parabolic cylinder or a hyperbolic cylinder. In this case the points at infinity of C are real (intersection of a real plane with real lines). Thus the plane sections of Q cannot be circles (neither ellipses).

If Q is a sphere, its intersection with the plane at infinity is the ombilic, and all plane sections are circles.

If Q is a surface of revolution, its intersection with the ombilic consists of a pair of complex conjugate points (which are double points). A real plane contains these two points if and only if it is perpendicular to the axis of revolution. Thus the circular sections are the plane sections by a plane perpendicular to the axis, that have at least two real points.

In the other cases, the intersection of Q with the ombilic consists of two different pairs of complex conjugate points. As C is a curve of degree two, its intersection with the plane at infinity consists of two points, possibly equal. The curve C is thus a circle, if these two points are one of these two pairs of complex conjugate points on the ombilic. Each of these pairs defines a real line (passing through the points), which is the intersection of P with the plane at infinity. Thus, one has a circular section if and only C has at least two real points and P contains one of these lines at infinity (that is if P is parallel to one of two directions defined by these lines at infinity).

Determination of circular sections of a quadric

In order to find the planes, which contain circular sections of a given quadric, one uses the following statements:

(S:) If the common points of a quadric with a sphere are contained in a pair of planes, then the intersection curve consists of two circles.

(P:) If the intersection of a plane and a quadric is a circle, then any parallel plane, that contains at least two points of the quadric, intersects the quadric in a circle, too.

Hence the strategy for the detection of circular sections is:

1) Find a sphere that intersects the quadric in a pair of planes and

2) The planes that are parallel to the detected ones deliver the remaining circular sections.

Tri-axial ellipsoid

tri-axial ellipsoid with circular sections (blue and green) and the auxiliary sphere (red), which intersects the quadric in the blue circles

Ellipsoid intersected by spheres: [math]\displaystyle{ c\lt {\color{seagreen}r_1}\lt {\color{blue}b}\lt {\color{purple}r_2}\lt a }[/math]

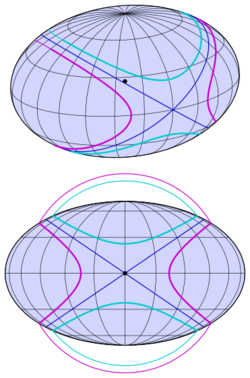
For the ellipsoid with equation

[math]\displaystyle{ \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 }[/math]

and the semi-axes [math]\displaystyle{ a\gt b\gt c\gt 0 }[/math] one uses an auxiliary sphere with equation

[math]\displaystyle{ x^2+y^2+z^2=r^2\ . }[/math]

The sphere's radius has to be chosen such that the intersection with the ellipsoid is contained in two planes through the origin. Multiplication of the ellipsoid's equation by [math]\displaystyle{ r^2 }[/math] and subtracting the sphere's equation yields:

[math]\displaystyle{ \left(\frac{r^2}{a^2}-1\right)\;x^2+\left(\frac{r^2}{b^2}-1\right)\;y^2+\left(\frac{r^2}{c^2}-1\right)\;z^2=0\ . }[/math]

This equation describes a pair of planes, if one of the 3 coefficients is zero. In case of [math]\displaystyle{ \ r=a\ }[/math] or [math]\displaystyle{ \ r=c\ }[/math] the equation is only fulfilled by either the x-axis or the z-axis. Only in case of [math]\displaystyle{ \ r=b\ }[/math] one gets a pair of planes with equation

• [math]\displaystyle{ \left(\frac{b^2}{a^2}-1\right)\;x^2+\left(\frac{b^2}{c^2}-1\right)\;z^2=0\ \quad \leftrightarrow \quad z=\pm \tfrac{c}{a}\sqrt{\tfrac{a^2-b^2}{b^2-c^2}}\; x \ , }[/math]

because only in this case the remaining coefficients have different signs (due to: [math]\displaystyle{ a\gt b\gt c }[/math]).

The diagram gives an impression of more common intersections between a sphere and an ellipsoid and highlights the exceptional circular case (blue).

If the values of the semi-axes are approaching, the two pencils of planes (and circles) approach either. For [math]\displaystyle{ a=b }[/math] all the planes are orthogonal to the z-axis (rotation axis).

Proof of property (P):
Turning the ellipsoid around the y-axis such that one of the two circles (blue) lies in the x-y-plane results in a new equation of the ellipsoid:

[math]\displaystyle{ Ax^2+By^2+Cz^2+D{\color{red}xz}=E }[/math]

For [math]\displaystyle{ z=0 }[/math] one gets [math]\displaystyle{ Ax^2+By^2=E }[/math], which has to be the equation of a circle. This is only true, if [math]\displaystyle{ A=B\ne 0,\ E\gt 0 }[/math]. The intersection of the ellipsoid by a plane with equation [math]\displaystyle{ z=z_0 }[/math], (parallel to the x-y-plane) has the equation

[math]\displaystyle{ A(x^2+y^2)+Dz_0 x=E-Cz_0^2 }[/math].

This equation describes a circle or a point or the empty set. Center and radius of the circle can be found be completing the square.

Elliptical hyperboloid of one sheet

hyperboloid of one sheet

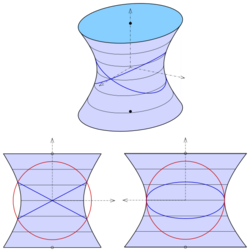
For the hyperboloid of one sheet with equation

[math]\displaystyle{ \frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1\ , \quad a\gt b\ , c\gt 0 }[/math]

analogously one gets for the intersection with the sphere [math]\displaystyle{ \ x^2+y^2+z^2=r^2\ }[/math] the equation

[math]\displaystyle{ \left(\frac{r^2}{a^2}-1\right)\;x^2+\left(\frac{r^2}{b^2}-1\right)\;y^2-\left(\frac{r^2}{c^2}+1\right)\;z^2=0\ . }[/math]

Only for [math]\displaystyle{ \ r=a\ }[/math] one gets a pair of planes:

[math]\displaystyle{ \left(\frac{a^2}{b^2}-1\right)\;y^2-\left(\frac{a^2}{c^2}+1\right)\;z^2=0\ \quad \leftrightarrow \quad z=\pm \frac{c}{b}\sqrt{\frac{a^2-b^2}{a^2+c^2}}\; y \ ,\ }[/math]

Elliptical cylinder

elliptical cylinder

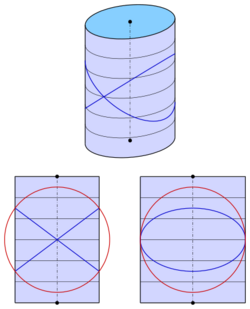
For the elliptical cylinder with equation

[math]\displaystyle{ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\ , \quad a\gt b\ , }[/math]

one gets the equation

[math]\displaystyle{ \left(\frac{r^2}{a^2}-1\right)\;x^2+\left(\frac{r^2}{b^2}-1\right)\;y^2-z^2=0\ . }[/math]

Only for [math]\displaystyle{ \ r=a\ }[/math] one gets a pair of planes:

[math]\displaystyle{ \left(\frac{a^2}{b^2}-1\right)\;y^2-z^2=0\ \quad \leftrightarrow \quad z=\pm \frac{\sqrt{a^2-b^2}}{b}\; y \ .\ }[/math]

Elliptical paraboloid

elliptical paraboloid

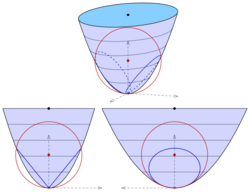
For the elliptical paraboloid with equation

[math]\displaystyle{ ax^2+by^2-z=0\ , \quad a{\color{red}{\lt }}b\ , }[/math]

one chooses a sphere containing the vertex (origin) and with center on the axis (z-axis) :

[math]\displaystyle{ x^2+y^2+(z-r)^2=r^2 \quad \leftrightarrow \quad x^2+y^2+z^2-2rz=0 \ . }[/math]

After elimination of the linear parts one gets the equation

[math]\displaystyle{ (2ra-1)\;x^2+(2rb-1)\;y^2-z^2=0\ . }[/math]

Only for [math]\displaystyle{ r=\tfrac{1}{2a} }[/math] one gets a pair of planes :

[math]\displaystyle{ \left(\frac{b}{a}-1\right)\; y^2-z^2=0 \quad \leftrightarrow \quad z=\pm \sqrt{\frac{b-a}{a}}\; y \ .\ }[/math]

Elliptical hyperboloid of two sheets

elliptical hyperboloid of two sheets

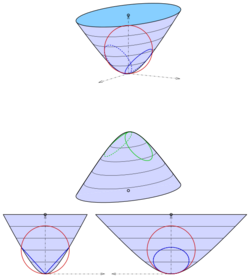
The hyperboloid of two sheets with equation

[math]\displaystyle{ -\frac{x^2}{a^2} - \frac{y^2}{b^2} +\frac{z^2}{c^2} = 1 \ ,\quad a\gt b \ , \ c\gt 0 \ , }[/math]

is shifted at first such that one vertex is the origin (s. diagram):

[math]\displaystyle{ -\frac{x^2}{a^2} - \frac{y^2}{b^2} +\frac{(z+c)^2}{c^2} = 1 \quad \leftrightarrow \quad \ -\frac{x^2}{a^2} - \frac{y^2}{b^2} +\frac{z^2}{c^2} +\frac{2z}{c} = 0 \ . }[/math]

Analogously to the paraboloid case one chooses a sphere containing the origin with center on the z-axis:

[math]\displaystyle{ x^2+y^2+(z-r)^2=r^2 \quad \leftrightarrow \quad x^2+y^2+z^2-2zr=0 \ . }[/math]

After elimination of the linear parts one gets the equation

[math]\displaystyle{ \left(-\frac{r}{a^2}+\frac{1}{c}\right)\;x^2+\left(-\frac{r}{b^2}+\frac{1}{c}\right)\;y^2 +\left(\frac{r}{c^2}+\frac{1}{c}\right)z^2=0\ . }[/math]

Only for [math]\displaystyle{ r=\tfrac{a^2}{c} }[/math] one gets a pair of planes:

[math]\displaystyle{ \left(-\frac{a^2}{b^2c}+\frac{1}{c}\right)\;y^2+\left(\frac{a^2}{c^3}+\frac{1}{c}\right)\;z^2=0\ \quad \leftrightarrow \quad z=\pm \frac{c}{b}\sqrt{\frac{a^2-b^2}{a^2+c^2}}\; y \ . }[/math]

Elliptical cone

elliptical cone

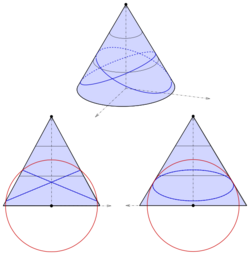
The elliptical cone with equation

[math]\displaystyle{ \frac{x^2}{a^2} + \frac{y^2}{b^2} -z^2= 0 \ ,\quad a\gt b \ , }[/math]

is shifted such that the vertex is not the origin (s. diagram):

[math]\displaystyle{ \frac{x^2}{a^2} + \frac{y^2}{b^2} -(z-1)^2= 0 \quad \leftrightarrow \quad \frac{x^2}{a^2} + \frac{y^2}{b^2} -z^2+2z= 1. }[/math]

Now a sphere with center at the origin is suitable:

[math]\displaystyle{ x^2+y^2+z^2=r^2 \ . }[/math]

Eliminatiion of [math]\displaystyle{ x^2 }[/math] yields:

[math]\displaystyle{ (\frac{a^2}{b^2}-1)\; y^2 -(1+a^2)\; z^2+2a^2z=a^2-r^2 \ . }[/math]

In this case completing the square gives:

[math]\displaystyle{ \frac{a^2-b^2}{b^2}\; y^2-(1+a^2)\left(z-\frac{a^2}{1+a^2}\right)^2 = a^2-\frac{a^4}{1+a^2}-r^2 \ . }[/math]

In order to get the equation of a pair of planes, the right part of the equation has to be zero, which is true for [math]\displaystyle{ r=\tfrac{a}{\sqrt{1+a^2}}\ . }[/math] The solution for z gives:

[math]\displaystyle{ z=\frac{a^2}{1+a^2}\pm\frac{1}{b}\sqrt{\frac{a^2-b^2}{1+a^2}}\; y \ . }[/math]

References

• H. F. Baker: Principles of Geometry, Volume 3, Cambridge University Press, 2010, ISBN:978-1-108-01779-4.
• D. M. Y. Sommerville: Analytical Geometry of Three Dimensions, Cambridge University Press, 1959, ISBN:978-1-316-60190-7, p. 204.
• K. P. Grotemeyer: Analytische Geometrie. Göschen-Verlag, 1962, p. 143.
• H. Scheid, W. Schwarz: Elemente der Linearen Algebra und der Analysis. Spektrum, Heidelberg, 2009, ISBN:978-3-8274-1971-2, p. 132.

External links

• H. Wiener, P. Treutlein: Models of a tri-axial ellipsoid and an elliptic paraboloid using circular sections (see p. 15) [1] (PDF).