Closure problem
In graph theory and combinatorial optimization, a closure of a directed graph is a set of vertices C, such that no edges leave C. The closure problem is the task of finding the maximum-weight or minimum-weight closure in a vertex-weighted directed graph.[1][2] It may be solved in polynomial time using a reduction to the maximum flow problem. It may be used to model various application problems of choosing an optimal subset of tasks to perform, with dependencies between pairs of tasks, one example being in open pit mining.
Algorithms
Condensation
The maximum-weight closure of a given graph G is the same as the complement of the minimum-weight closure on the transpose graph of G, so the two problems are equivalent in computational complexity. If two vertices of the graph belong to the same strongly connected component, they must behave the same as each other with respect to all closures: it is not possible for a closure to contain one vertex without containing the other. For this reason, the input graph to a closure problem may be replaced by its condensation, in which every strongly connected component is replaced by a single vertex. The condensation is always a directed acyclic graph.
Reduction to maximum flow
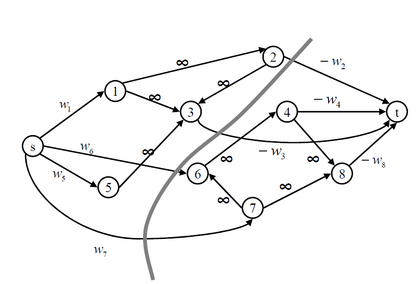
As (Picard 1976) showed,[2][3] a maximum-weight closure may be obtained from G by solving a maximum flow problem on a graph H constructed from G by adding to it two additional vertices s and t. For each vertex v with positive weight in G, the augmented graph H contains an edge from s to v with capacity equal to the weight of v, and for each vertex v with negative weight in G, the augmented graph H contains an edge from v to t whose capacity is the negation of the weight of v. All of the edges in G are given infinite capacity in H.[1]
A minimum cut separating s from t in this graph cannot have any edges of G passing in the forward direction across the cut: a cut with such an edge would have infinite capacity and would not be minimum. Therefore, the set of vertices on the same side of the cut as s automatically forms a closure C. The capacity of the cut equals the weight of all positive-weight vertices minus the weight of the vertices in C, which is minimized when the weight of C is maximized. By the max-flow min-cut theorem, a minimum cut, and the optimal closure derived from it, can be found by solving a maximum flow problem.[1]
Alternative algorithms
Alternative algorithms for the maximum closure problem that do not compute flows have also been studied.[4][5][6] Their running time is similar to that of the fastest known flow algorithms.[4]
Applications
Open pit mining
An open pit mine may be modeled as a set of blocks of material which may be removed by mining it once all the blocks directly above it have been removed. A block has a total value, equal to the value of the minerals that can be extracted from it minus the cost of removal and extraction; in some cases, a block has no extraction value but must still be removed to reach other blocks, giving it a negative value. One may define an acyclic network that has as its vertices the blocks of a mine, with an edge from each block to the blocks above it that must be removed earlier than it. The weight of each vertex in this network is the total value of its block, and the most profitable plan for mining can be determined by finding a maximum weight closure, and then forming a topological ordering of the blocks in this closure.[1][5][7]
Military targeting
In military operations, high-value targets such as command centers are frequently protected by layers of defense systems, which may in turn be protected by other systems. In order to reach a target, all of its defenses must be taken down, making it into a secondary target. Each target needs a certain amount of resources to be allocated to it in order to perform a successful attack. The optimal set of targets to attack, to obtain the most value for the resources expended, can be modeled as a closure problem.[1][8]
Transportation network design
The problem of planning a freight delivery system may be modeled by a network in which the vertices represent cities and the (undirected) edges represent potential freight delivery routes between pairs of cities. Each route can achieve a certain profit, but can only be used if freight depots are constructed at both its ends, with a certain cost. The problem of designing a network that maximizes the difference between the profits and the costs can be solved as a closure problem, by subdividing each undirected edge into two directed edges, both directed outwards from the subdivision point. The weight of each subdivision point is a positive number, the profit of the corresponding route, and the weight of each original graph vertex is a negative number, the cost of building a depot in that city.[1]Cite error: Closing </ref> missing for <ref> tag[9]
Although (as Lawler shows) this scheduling problem is NP-complete in general, Sidney describes a decomposition method that can help solve the problem by reducing it to several smaller problems of the same type. In particular, if S is a subset of the tasks that (among all subsets) has the largest possible ratio of its total weight to its total processing time, and in addition S is minimal among all sets with the same ratio, then there exists an optimal schedule in which all tasks in S are performed before all other tasks. As long as S is not the whole set of tasks, this partition of the tasks splits the scheduling problem into two smaller problems, one of scheduling S and one of scheduling the remaining tasks.[10] Although S is a closure (for a graph with reversed edges from G) the problem of finding S is not exactly a maximum weight closure problem, because the value of S is a ratio rather than a sum of weights. Nevertheless, Lawler shows that S may be found in polynomial time by a binary search algorithm in which each step of the search uses an instance of the closure problem as a subroutine.[9]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 "19.2 Maximum weight closure of a graph", Network flows, Englewood Cliffs, NJ: Prentice Hall Inc., 1993, pp. 719–724, ISBN 0-13-617549-X.
- ↑ 2.0 2.1 "Optimal closure in a digraph", Combinatorial Optimization, Wiley Series in Discrete Mathematics and Optimization, 33, John Wiley & Sons, 2011, pp. 49–50, ISBN 9781118031391, https://books.google.com/books?id=tarLTNwM3gEC&pg=PA49.
- ↑ Picard, Jean-Claude (1976), "Maximal closure of a graph and applications to combinatorial problems", Management Science 22 (11): 1268–1272, doi:10.1287/mnsc.22.11.1268.
- ↑ 4.0 4.1 "A new-old algorithm for minimum-cut and maximum-flow in closure graphs", Networks 37 (4): 171–193, 2001, doi:10.1002/net.1012.
- ↑ 5.0 5.1 Lerchs, H.; Grossmann, I. F. (1965), "Optimum design of open-pit mines", Transactions of the Canadian Institute of Mining and Metallurgy 68: 17–24. As cited by (Hochbaum 2001).
- ↑ Faaland, Bruce; Kim, Kiseog; Schmitt, Tom (1990), "A new algorithm for computing the maximal closure of a graph", Management Science 36 (3): 315–331, doi:10.1287/mnsc.36.3.315.
- ↑ Johnson, T. B. (1968), Optimum pit mine production scheduling, Technical Report, University of California, Berkeley, CA. As cited by (Ahuja Magnanti).
- ↑ Orlin, D. (1987), "Optimal weapons allocation against layered defenses", Naval Research Logistics Quarterly 34 (5): 605–617, doi:10.1002/1520-6750(198710)34:5<605::aid-nav3220340502>3.0.co;2-l. As cited by (Ahuja Magnanti).
- ↑ 9.0 9.1 "Sequencing jobs to minimize total weighted completion time subject to precedence constraints", Ann. Discrete Math., Annals of Discrete Mathematics 2: 75–90, 1978, doi:10.1016/S0167-5060(08)70323-6, ISBN 9780720410433, https://books.google.com/books?id=YvdjzQxSMLMC&pg=PA75.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedsidney75
 |
