Cofunction
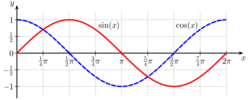
In mathematics, a function f is cofunction of a function g if f(A) = g(B) whenever A and B are complementary angles (pairs that sum to one right angle).[1] This definition typically applies to trigonometric functions.[2][3] The prefix "co-" can be found already in Edmund Gunter's Canon triangulorum (1620).[4][5]
For example, sine (Latin: sinus) and cosine (Latin: cosinus,[4][5] sinus complementi[4][5]) are cofunctions of each other (hence the "co" in "cosine"):
| [math]\displaystyle{ \sin\left(\frac{\pi}{2} - A\right) = \cos(A) }[/math][1][3] | [math]\displaystyle{ \cos\left(\frac{\pi}{2} - A\right) = \sin(A) }[/math][1][3] |
The same is true of secant (Latin: secans) and cosecant (Latin: cosecans, secans complementi) as well as of tangent (Latin: tangens) and cotangent (Latin: cotangens,[4][5] tangens complementi[4][5]):
| [math]\displaystyle{ \sec\left(\frac{\pi}{2} - A\right) = \csc(A) }[/math][1][3] | [math]\displaystyle{ \csc\left(\frac{\pi}{2} - A\right) = \sec(A) }[/math][1][3] |
| [math]\displaystyle{ \tan\left(\frac{\pi}{2} - A\right) = \cot(A) }[/math][1][3] | [math]\displaystyle{ \cot\left(\frac{\pi}{2} - A\right) = \tan(A) }[/math][1][3] |
These equations are also known as the cofunction identities.[2][3]
This also holds true for the versine (versed sine, ver) and coversine (coversed sine, cvs), the vercosine (versed cosine, vcs) and covercosine (coversed cosine, cvc), the haversine (half-versed sine, hav) and hacoversine (half-coversed sine, hcv), the havercosine (half-versed cosine, hvc) and hacovercosine (half-coversed cosine, hcc), as well as the exsecant (external secant, exs) and excosecant (external cosecant, exc):
| [math]\displaystyle{ \operatorname{ver}\left(\frac{\pi}{2} - A\right) = \operatorname{cvs}(A) }[/math][6] | [math]\displaystyle{ \operatorname{cvs}\left(\frac{\pi}{2} - A\right) = \operatorname{ver}(A) }[/math] |
| [math]\displaystyle{ \operatorname{vcs}\left(\frac{\pi}{2} - A\right) = \operatorname{cvc}(A) }[/math][7] | [math]\displaystyle{ \operatorname{cvc}\left(\frac{\pi}{2} - A\right) = \operatorname{vcs}(A) }[/math] |
| [math]\displaystyle{ \operatorname{hav}\left(\frac{\pi}{2} - A\right) = \operatorname{hcv}(A) }[/math] | [math]\displaystyle{ \operatorname{hcv}\left(\frac{\pi}{2} - A\right) = \operatorname{hav}(A) }[/math] |
| [math]\displaystyle{ \operatorname{hvc}\left(\frac{\pi}{2} - A\right) = \operatorname{hcc}(A) }[/math] | [math]\displaystyle{ \operatorname{hcc}\left(\frac{\pi}{2} - A\right) = \operatorname{hvc}(A) }[/math] |
| [math]\displaystyle{ \operatorname{exs}\left(\frac{\pi}{2} - A\right) = \operatorname{exc}(A) }[/math] | [math]\displaystyle{ \operatorname{exc}\left(\frac{\pi}{2} - A\right) = \operatorname{exs}(A) }[/math] |
See also
- Hyperbolic functions
- Lemniscatic cosine
- Jacobi elliptic cosine
- Cologarithm
- Covariance
- List of trigonometric identities
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). "Chapter II. The Acute Angle [10 Functions of complementary angles"]. Trigonometry. Part I: Plane Trigonometry. New York: Henry Holt and Company. pp. 11–12. https://archive.org/stream/planetrigonometr00hallrich#page/n26/mode/1up.
- ↑ 2.0 2.1 Algebra and Trigonometry (8 ed.). Cengage Learning. 2014. p. 528. ISBN 978-128596583-3. https://books.google.com/books?id=JEDAAgAAQBAJ&pg=PA528. Retrieved 2017-07-28.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 3.7 "5.1 The Elementary Identities". Precalculus. 2012. http://jwbales.home.mindspring.com/precal/part5/part5.1.html.
- ↑ 4.0 4.1 4.2 4.3 4.4 Canon triangulorum. 1620.
- ↑ 5.0 5.1 5.2 5.3 5.4 Roegel, Denis, ed (2010-12-06). "A reconstruction of Gunter's Canon triangulorum (1620)". HAL. https://hal.inria.fr/inria-00543938/document.
- ↑ "Coversine". MathWorld. Wolfram Research, Inc.. http://mathworld.wolfram.com/Coversine.html.
- ↑ "Covercosine". MathWorld. Wolfram Research, Inc.. http://mathworld.wolfram.com/Covercosine.html.
 |  |
