Commandino's theorem
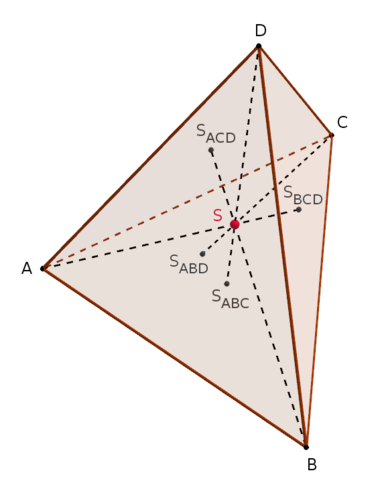
Commandino's theorem, named after Federico Commandino (1509–1575), states that the four medians of a tetrahedron are concurrent at a point S, which divides them in a 3:1 ratio. In a tetrahedron a median is a line segment that connects a vertex with the centroid of the opposite face – that is, the centroid of the opposite triangle. The point S is also the centroid of the tetrahedron.[1][2][3]
History
The theorem is attributed to Commandino, who stated, in his work De Centro Gravitatis Solidorum (The Center of Gravity of Solids, 1565), that the four medians of the tetrahedron are concurrent. However, according to the 19th century scholar Guillaume Libri, Francesco Maurolico (1494–1575) claimed to have found the result earlier. Libri nevertheless thought that it had been known even earlier to Leonardo da Vinci, who seemed to have used it in his work. Julian Coolidge shared that assessment but pointed out that he couldn't find any explicit description or mathematical treatment of the theorem in da Vinci's works.[4] Other scholars have speculated that the result may have already been known to Greek mathematicians during antiquity.[5]
Generalizations
Commandino's theorem has a direct analog for simplexes of any dimension:[6]
- Let be a -simplex of some dimension in and let be its vertices. Furthermore, let , be the medians of , the lines joining each vertex with the centroid of the opposite -dimensional facet . Then, these lines intersect each other in a point , in a ratio of .
Full generality
The former analog is easy to prove via the following, more general result, which is analogous to the way levers in physics work:[7]
- Let and be natural numbers, so that in an -vector space , pairwise different points are given.
- Let be the centroid of the points , let be the centroid of the points , and let be the centroid of all of these points.
- Then, one has
- In particular, the centroid lies on the line and divides it in a ratio of .
Reusch's theorem
The previous theorem has further interesting consequences other than the aforementioned generalization of Commandino's theorem. It can be used to prove the following theorem about the centroid of a tetrahedron, first described in the Mathematische Unterhaltungen by the German physicist Friedrich Eduard Reusch (de):[8][9]
- One may find the centroid of a tetrahedron by taking the midpoints of two pairs of two of its opposite edges and connecting the corresponding midpoints through their respective midline. The intersection point of both midlines will be the centroid of the tetrahedron.
Since a tetrahedron has six edges in three opposite pairs, one obtains the following corollary:[8]
- In a tetrahedron, the three midlines corresponding to opposite edge midpoints are concurrent, and their intersection point is the centroid of the tetrahedron.
Varignon's theorem
A specific case of Reusch's theorem where all four vertices of a tetrahedron are coplanar and lie on a single plane, thereby degenerating into a quadrilateral, Varignon's theorem, named after Pierre Varignon, states the following:[10][11]
- Let a quadrilateral in be given. Then the two midlines connecting opposite edge midpoints intersect in the centroid of the quadrilateral and are divided in half by it.
References
- ↑ Claudi Alsina, Roger B. Nelsen: A Mathematical Space Odyssey: Solid Geometry in the 21st Century. The Mathematical Association of America, 2015, ISBN 9780883853580, pp. 97–98
- ↑ Nathan Altshiller-Court: The Tetrahedron and Its Circumscribed Parallelepiped. The Mathematics Teacher, Vol. 26, No. 1 (JANUARY 1933), pp. 46–52 (JSTOR)
- ↑ Norman Schaumberger: Commandino's theorem. The Two-Year College Mathematics Journal, Vol. 13, No. 5 (Nov., 1982), p. 331 (JSTOR)
- ↑ Nathan Altshiller Court: Notes on the centroid. The Mathematics Teacher, Vol. 53, No. 1 (JANUARY 1960), pp. 34 (JSTOR)
- ↑ Howard Eves: Great Moments in Mathematics (before 1650). MAA, 1983, ISBN 9780883853108, p. 225
- ↑ Egbert Harzheim (1978) (in de). Einführung in die kombinatorische Topologie. Darmstadt: Wissenschaftliche Buchgesellschaft. pp. 33. ISBN 3-534-07016-X.
- ↑ Egbert Harzheim (1978) (in de), Einführung in die Kombinatorische Topologie, Darmstadt, p. 31, ISBN 3-534-07016-X
- ↑ 8.0 8.1 Friedrich Joseph Pythagoras Riecke (Hrsg.): Mathematische Unterhaltungen. Zweites Heft. 1973, S. 100, 128
- ↑ In den Mathematische Unterhaltungen (Zweites Heft, S. 128) wird auf die S. 36 von Reuschs Abhandlung Der Spitzbogen verwiesen.
- ↑ Coxeter, op. cit., S. 242
- ↑ DUDEN: Rechnen und Mathematik. 1985, S. 652
External links
- Weisstein, Eric W.. "Commandino's Theorem". http://mathworld.wolfram.com/CommandinosTheorem.html.
- A Couple of Nice Extensions of the Median Properties
 |
