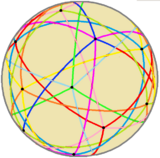
Compound of ten tetrahedra
| Compound of ten tetrahedra | |
|---|---|
| |
| Type | regular compound |
| Coxeter symbol | 2{5,3}[10{3,3}]2{3,5}[1] |
| Index | UC6, W25 |
| Elements (As a compound) |
10 tetrahedra: F = 40, E = 60, V = 20 |
| Dual compound | Self-dual |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | chiral tetrahedral (T) |
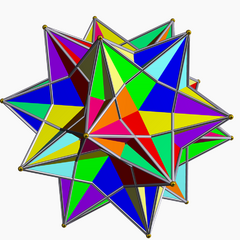
File:Compound of ten tetrahedra (full).stl The compound of ten tetrahedra is one of the five regular polyhedral compounds. This polyhedron can be seen as either a stellation of the icosahedron or a compound. This compound was first described by Edmund Hess in 1876.
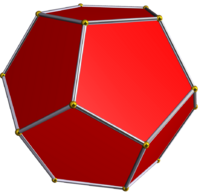
It can be seen as a faceting of a regular dodecahedron.
As a compound
It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry (Ih). It is one of five regular compounds constructed from identical Platonic solids.
It shares the same vertex arrangement as a dodecahedron.
The compound of five tetrahedra represents two chiral halves of this compound (it can therefore be seen as a "compound of two compounds of five tetrahedra").
It can be made from the compound of five cubes by replacing each cube with a stella octangula on the cube's vertices (which results in a "compound of five compounds of two tetrahedra").
As a stellation
This polyhedron is a stellation of the icosahedron, and given as Wenninger model index 25.
| Stellation diagram | Stellation core | Convex hull |
|---|---|---|

|
 Icosahedron |
 Dodecahedron |
As a facetting
It is also a facetting of the dodecahedron, as shown at left. Concave pentagrams can be seen on the compound where the pentagonal faces of the dodecahedron are positioned.
As a simple polyhedron
If it is treated as a simple non-convex polyhedron without self-intersecting surfaces, it has 180 faces (120 triangles and 60 concave quadrilaterals), 122 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, and 20 with degree 12), and 300 edges, giving an Euler characteristic of 122-300+180 = +2.
See also
References
- ↑ Regular polytopes, p.98
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3 (1st Edn University of Toronto (1938))
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN:0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
External links
- Weisstein, Eric W.. "Tetrahedron 10-Compound". http://mathworld.wolfram.com/Tetrahedron10-Compound.html.
- VRML model: [1]
- Compounds of 5 and 10 Tetrahedra by Sándor Kabai, The Wolfram Demonstrations Project.
- Klitzing, Richard. "3D compound". https://bendwavy.org/klitzing/dimensions/../incmats/e.htm.
 |