Convergent-beam electron diffraction

From HandWiki
Short description: Convergent beam electron diffraction technique

Convergent beam electron diffraction (CBED) is a diffraction technique where a convergent or divergent beam (conical electron beam) of electrons is used to study materials.

Schematic of the convergent beam electron diffraction technique. Adapted from W. Kossel & G. Möllenstedt, 1939.

History

This technique was first introduced in 1939 by Kossel and Möllenstedt, who worked with large (~40 μm) probes and small convergence angles.[1] The development of the Field Emission Gun (FEG) in the 1970s,[2] the Scanning Transmission Electron Microscopy (STEM), energy filtering devices and so on, made possible smaller probe diameters and larger convergence angles, and all this made CBED more popular. In the seventies, CBED was being used for the determination of the point group and space group symmetries by Goodman and Lehmpfuh,[3] Steeds,[4] Incorrect reference here Buxton[5] and starting on 1985, by Tanaka et al. by using different techniques of CBED which covered different applications.[6][7][8][9]

Applications

By using CBED, different types of information can be obtained:

  • crystal structural parameters such as lattice parameters,[10] sample thickness[11]
  • strain information[12]
  • defects such as stacking faults,[13] dislocations,[14] grain boundaries,[15] 3-dimensional deformations, lattice displacements[16]
  • crystal symmetry information - by looking at the symmetries that appear in the disks, point group[17] and space group determination is performed.[18][19]

Main parameters

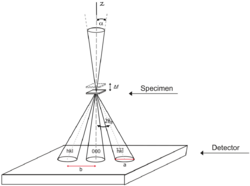
In CBED, the diameter of the electron beam is relatively small, usually 1–100 nm. This small diameter of the beam in real space, opens up a greater angular range in reciprocal space. Consequently, instead of diffraction peaks, diffraction disks are seen. The beam semi-convergence angle, α, is of the order of milliradians, ranging from 0.1˚ - 1˚.[20] For small semi-convergence angle, the disks do not overlap with each-other, whereas for larger semi-convergence angles, the disks overlap.[21] When a CBED pattern is formed, there are some variables that need to be controlled:

  • the beam semi-convergence angle α - is controlled by the C2 aperture. The size of the diffraction disks depends on α:

2α = 2θ B a/b

where θB is the Bragg angle of the specimen, a is the width of the diffraction disks and b is the distance between the 000 disk and the hkl disks (see Figure).

  • the focus of the pattern – in a Transmission Electron Microscope (TEM), the image is focused when the specimen is at eucentric height, so one way to defocus the image is by moving the specimen up or down in the z direction. The distance between the crossover of the incident beam and the z position of the specimen is called defocus distance Δf. In exact focus, no spatial information is present in the CBED discs. At a defocus distance, both the direct space and reciprocal space information will start to be visible in the CBED pattern.[22]

CBED and the related techniques

A CBED pattern can be obtained by many different techniques, such as:

  • Conventional (C)TEM-CBED. In CTEM-CBED different shape condenser apertures are used to obtain the intensity distribution over the entire Brillouin zone.[23]
  • Large Angle (LA)CBED - is performed with a large incident angle, ranging from 1˚ - 10˚. LACBED makes it possible to obtain non-overlapping disks with larger diameter than the one determined by the Bragg angle. With LACBED I one can obtain one selected CBED disk at a time on a detector.[24] In LACBED II, with a slight change in the focusing conditions of the intermediate lens, bright field patterns and dark field patterns can be obtained simultaneously, without overlapping each-other on the fluorescent screen.[25] A disadvantage of LACBED is that it requires a large flat specimen.
  • 4D-STEM - in this technique a beam is raster scanned on a specimen in a 2D array and in each position of the array, a 2D diffraction pattern is obtained, thus generating a 4D data set. After acquisition, by using different phase techniques such as ptychography, one can recover the transmittion function and the induced phase-shift.[26] In some application, 4D-STEM is called STEM-CBED.[27]
  • Beam Rocking (BR)-CBED - with this technique, by rocking the incident beam with a rocking coil placed above the specimen, a virtual convergent beam is produced. Given that the diameter of the beam on the specimen is few micrometers, this method has made CBED possible to materials that are susceptible to strong convergent beams. Furthermore, the large size of the illuminated specimen area and the low density current of the beam make specimen contamination insignificant.[28][29]
  • BR-LACBED - in this technique, additionally to the rocking coil above the specimen, there is a rocking coil placed under the projector lens, which is used to bring the preferred beam to the STEM detector. Every time the incident beam is being rocked, the second coil is simultaneously driven so that the beam always falls on the STEM detector.[30]
  • Signal processing and BR-CBED - in order to enhance contrast in BR-CBED, a band-pass filter can be used which filters a certain frequency band in the CBED pattern. The combination of these two techniques makes the symmetries appearing in the patterns more clear.[31]
  • CB-LEED (Low Energy Electron Diffraction) - rocking curves are analyzed at a single energy using a convergent probe.[32] Advantages of this method are: mapping of LEED diffraction spots into CBLEED disks, the diffraction patterns originate from a localized region of the specimen which enables extraction of localized structural information,[33] mapping out of the surfaces, sensitivity enhancement of small atomic displacements etc.[34]
  • Ptychography is a technique for recovering the phase of the exit electron wave. The reconstruction is done by applying an iterative phase retrieval algorithm which returns a real-space image with both phase and amplitude information. By using electron ptychography, in 2018, images of MoS2 with atomic resolution of 0.39 Å were reported by Jiang et al. which set the new world record in highest resolution microscope.[35][36]

Relation to other techniques

In literature, there are used several terms referring to electron diffraction patterns that are acquired with a convergent beam. Such terms are CBED, microdiffraction, nanodiffraction etc. When the CBED technique is used for the acquisition of conventional diffraction information like lattice structure, interplanar spacing from very small areas, then the term microdiffraction is used.[37] On the other hand, the term nanodiffraction is used when there are used very small probes (< 1 nm or less in diameter).[38][39]

Advantages and disadvantages of CBED

Since the diameter of the convergent beam is smaller than the parallel one, most of the obtained information from CBED is generated from very small regions, where other methods cannot reach. For example, in Selected Area Electron Diffraction (SAED), where a parallel beam illumination is used, the smallest area that can be selected is 0.5 µm at 100 kV, whereas in CBED is possible to go to areas smaller than 100 nm.[40] Also, the amount of information that is obtained from a CBED pattern is larger than that from a SAED pattern. Nonetheless, CBED has also its disadvantages. The focused probe may generate contamination which can cause localized stresses. But this was more of a problem in the past and now with the high vacuum conditions, one should be able to probe a clean region of the specimen from minutes to hours. Another disadvantage is that the convergent beam may heat or damage the chosen region of the specimen.[41] Since 1939, CBED has been mainly used to study thicker materials. Recently, work on 2D monolayer crystals and van der Waals structures has been conducted, where deformations at a nanometer resolution have been retrieved, the interlayer distance of a bilayer crystal has been reconstructed and so on by using CBED.[42]

References

  1. ↑ Kossel, W.; Möllenstedt, G. (1939). "Elektroneninterferenzen im konvergenten Bündel". Annalen der Physik 428 (2): 113–140. doi:10.1002/andp.19394280204. Bibcode: 1939AnP...428..113K. 
  2. ↑ Crewe, A. V.; Isaacson, M.; Johnson, D. (February 1969). "A Simple Scanning Electron Microscope". Review of Scientific Instruments 40 (2): 241–246. doi:10.1063/1.1683910. Bibcode: 1969RScI...40..241C. https://digital.library.unt.edu/ark:/67531/metadc1061663/. 
  3. ↑ Goodman, P.; Lehmpfuhl, G. (1 May 1968). "Observation of the breakdown of Friedel's law in electron diffraction and symmetry determination from zero-layer interactions". Acta Crystallographica Section A 24 (3): 339–347. doi:10.1107/S0567739468000677. Bibcode: 1968AcCrA..24..339G. 
  4. ↑ Hren, John J (1979). Introduction to Analytical Electron Microscopy. Boston, MA. ISBN 147575583X. 
  5. ↑ Buxton, B. F.; Eades, J. A.; Steeds, John Wickham; Rackham, G. M.; Frank, Frederick Charles (11 March 1976). "The symmetry of electron diffraction zone axis patterns". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 281 (1301): 171–194. doi:10.1098/rsta.1976.0024. Bibcode: 1976RSPTA.281..171B. https://doi.org/10.1098/rsta.1976.0024. 
  6. ↑ Tanaka, Michiyoshi; Terauchi, Masami (1985). Convergent-Beam Electron Diffraction I. JEOL Ltd. 
  7. ↑ Tanaka, Michiyoshi; Terauchi, Masami (1988). Convergent beam electron diffraction II. JEOL Ltd. 
  8. ↑ Tanaka, Michiyoshi; Terauchi, Masami; Tsuda, Kenji (1994). Convergent beam electron diffraction III. JEOL Ltd. 
  9. ↑ Tanaka, Michiyoshi; Terauchi, Masami; Tsuda, Kenji; Saitoh, Koh (2002). Convergent beam electron diffraction IV. 
  10. ↑ Jones, P. M.; Rakham, G. M.; Steeds, John Wick (30 May 1977). "Higher order Laue zone effects in electron diffraction and their use in lattice parameter determination". Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences 354 (1677): 197–222. doi:10.1098/rspa.1977.0064. Bibcode: 1977RSPSA.354..197J. 
  11. ↑ Kelly, P. M.; Jostsons, A.; Blake, R. G.; Napier, J. G. (16 October 1975). "The determination of foil thickness by scanning transmission electron microscopy". Physica Status Solidi A 31 (2): 771–780. doi:10.1002/pssa.2210310251. Bibcode: 1975PSSAR..31..771K. 
  12. ↑ Clément, L.; Pantel, R.; Kwakman, L. F. Tz.; Rouvière, J. L. (26 July 2004). "Strain measurements by convergent-beam electron diffraction: The importance of stress relaxation in lamella preparations". Applied Physics Letters 85 (4): 651–653. doi:10.1063/1.1774275. Bibcode: 2004ApPhL..85..651C. 
  13. ↑ Morniroli, J. P. (September 2006). "CBED and LACBED characterization of crystal defects". Journal of Microscopy 223 (3): 240–245. doi:10.1111/j.1365-2818.2006.01630.x. PMID 17059540. 
  14. ↑ Carpenter, R. W.; Spence, J. C. H. (1 January 1982). "Three-dimensional strain-field information in convergent-beam electron diffraction patterns". Acta Crystallographica Section A 38 (1): 55–61. doi:10.1107/S0567739482000102. Bibcode: 1982AcCrA..38...55C. 
  15. ↑ Wu, Lijun; Zhu, Yimei; Tafto, J.; Welch, D. O.; Suenaga, M. (19 September 2002). "Quantitative analysis of twist boundaries and stacking faults in Bi-based superconductors by parallel recording of dark-field images with a coherent electron source". Physical Review B 66 (10): 104517. doi:10.1103/PhysRevB.66.104517. Bibcode: 2002PhRvB..66j4517W. 
  16. ↑ Wu, Lijun; Zhu, Yimei; Tafto, J. (11 December 2000). "Picometer Accuracy in Measuring Lattice Displacements Across Planar Faults by Interferometry in Coherent Electron Diffraction". Physical Review Letters 85 (24): 5126–5129. doi:10.1103/PhysRevLett.85.5126. PMID 11102202. Bibcode: 2000PhRvL..85.5126W. 
  17. ↑ Tanaka, M.; Saito, R.; Sekii, H. (1 May 1983). "Point-group determination by convergent-beam electron diffraction". Acta Crystallographica Section A: Foundations of Crystallography 39 (3): 357–368. doi:10.1107/S010876738300080X. 
  18. ↑ Goodman, P. (1 November 1975). "A practical method of three-dimensional space-group analysis using convergent-beam electron diffraction". Acta Crystallographica Section A 31 (6): 804–810. doi:10.1107/S0567739475001738. Bibcode: 1975AcCrA..31..804G. 
  19. ↑ Tanaka, M.; Sekii, H.; Nagasawa, T. (1 November 1983). "Space-group determination by dynamic extinction in convergent-beam electron diffraction". Acta Crystallographica Section A: Foundations of Crystallography 39 (6): 825–837. doi:10.1107/S0108767383001695. 
  20. ↑ Tanaka, Michiyoshi; Terauchi, Masami (1985). Convergent-Beam Electron Diffraction I. 
  21. ↑ Morniroli, J. P. (2006). "CBED and LACBED characterization of crystal defects" (in en). Journal of Microscopy 223 (3): 240–245. doi:10.1111/j.1365-2818.2006.01630.x. ISSN 1365-2818. PMID 17059540. https://onlinelibrary.wiley.com/doi/10.1111/j.1365-2818.2006.01630.x. 
  22. ↑ Cowley, J. M. (1987). Advances in electronics and electron physics. 
  23. ↑ Tanaka, Michiyoshi (1986). "Conventional Transmission-Electron-Microscopy Techniques in Convergent-Beam Electron Diffraction". Journal of Electron Microscopy. doi:10.1093/oxfordjournals.jmicro.a050584. 
  24. ↑ Tanaka, Michiyoshi; Saito, Ryuichi; Ueno, Katsuyoshi; Harada, Yoshiyasu (1980). "Large-Angle Convergent-Beam Electron Diffraction". Journal of Electron Microscopy. doi:10.1093/oxfordjournals.jmicro.a050262. 
  25. ↑ Tanaka, Michiyoshi; Terauchi, Masami (1985). Convergent-Beam Electron Diffraction I. 
  26. ↑ O'Leary, C. M.; Allen, C. S.; Huang, C.; Kim, J. S.; Liberti, E.; Nellist, P. D.; Kirkland, A. I. (23 March 2020). "Phase reconstruction using fast binary 4D STEM data". Applied Physics Letters 116 (12): 124101. doi:10.1063/1.5143213. Bibcode: 2020ApPhL.116l4101O. https://ora.ox.ac.uk/objects/uuid:fda0236e-162d-4cd7-b91a-11ca5211d8c2. 
  27. ↑ Tsuda, Kenji; Yasuhara, Akira; Tanaka, Michiyoshi (19 August 2013). "Two-dimensional mapping of polarizations of rhombohedral nanostructures in the tetragonal phase of BaTiO 3 by the combined use of the scanning transmission electron microscopy and convergent-beam electron diffraction methods". Applied Physics Letters 103 (8): 082908. doi:10.1063/1.4819221. Bibcode: 2013ApPhL.103h2908T. 
  28. ↑ van Oostrum, K. J.; Leenhouts, A.; Jore, A. (September 1973). "A new scanning microdiffraction technique". Applied Physics Letters 23 (5): 283–284. doi:10.1063/1.1654890. Bibcode: 1973ApPhL..23..283V. 
  29. ↑ Tanaka, Michiyoshi; Terauchi, Masami (1985). Convergent-Beam Electron Diffraction I. 
  30. ↑ TANAKA, Michiyoshi; SAITO, Ryuichi; UENO, Katsuyoshi; HARADA, Yoshiyasu (1 January 1980). "Large-Angle Convergent-Beam Electron Diffraction". Journal of Electron Microscopy 29 (4): 408–412. doi:10.1093/oxfordjournals.jmicro.a050262. ISSN 0022-0744. https://academic.oup.com/jmicro/article/29/4/408/882709/LargeAngle-ConvergentBeam-Electron-Diffraction. 
  31. ↑ Tanaka, Michiyoshi; Ueno, Katsuyoshi; Hirata, Yoshihiro (April 1980). "Signal Processing of Convergent-Beam Electron Diffraction Patterns Obtained by the Beam-Rocking Method". Japanese Journal of Applied Physics 19 (4): L201–L204. doi:10.1143/JJAP.19.L201. Bibcode: 1980JaJAP..19L.201T. 
  32. ↑ Spence, J.C.H.; Poon, H.C.; Saldin, D.K. (February 2004). "Convergent-Beam Low Energy Electron Diffraction (CBLEED) and the Measurement of Surface Dipole Layers". Microscopy and Microanalysis 10 (1): 128–133. doi:10.1017/S1431927604040346. PMID 15306076. Bibcode: 2004MiMic..10..128S. 
  33. ↑ Ruben, G.; Jesson, D.E.; Paganin, D.M.; Smith, A.E. (May 2009). "Kinematic simulation of convergent beam low-energy electron diffraction patterns". Optik 120 (9): 401–408. doi:10.1016/j.ijleo.2007.10.006. Bibcode: 2009Optik.120..401R. 
  34. ↑ Constantinou, Procopios C.; Jesson, David E. (September 2019). "On the sensitivity of convergent beam low energy electron diffraction patterns to small atomic displacements". Applied Surface Science 489: 504–509. doi:10.1016/j.apsusc.2019.05.274. Bibcode: 2019ApSS..489..504C. 
  35. ↑ Jiang, Yi; Chen, Zhen; Han, Yimo; Deb, Pratiti; Gao, Hui; Xie, Saien; Purohit, Prafull; Tate, Mark W. et al. (July 2018). "Electron ptychography of 2D materials to deep sub-ångström resolution". Nature 559 (7714): 343–349. doi:10.1038/s41586-018-0298-5. PMID 30022131. Bibcode: 2018Natur.559..343J. 
  36. ↑ "Highest resolution microscope". Guinness World Records. https://www.guinnessworldrecords.com/world-records/highest-resolution-microscope. 
  37. ↑ Carpenter, R. W.; Spence, J. C. H. (November 1984). "Applications of modern microdiffraction to materials science". Journal of Microscopy 136 (2): 165–178. doi:10.1111/j.1365-2818.1984.tb00526.x. 
  38. ↑ Williams, David B. (2009). Transmission electron microscopy : a textbook for materials science (2nd ed.). New York: Springer. ISBN 978-0-387-76501-3. 
  39. ↑ Steeds, John Wickham; Hren, J. J.; Goldstein, J. I.; Joy, D. C. (1979). Introduction to Analytical Electron Microscopy. Plenum Press. pp. 387. 
  40. ↑ Champness, P. E. (March 1987). "Convergent beam electron diffraction". Mineralogical Magazine 51 (359): 33–48. doi:10.1180/minmag.1987.051.359.04. Bibcode: 1987MinM...51...33C. 
  41. ↑ Williams, David B. (2009). Transmission electron microscopy : a textbook for materials science (2nd ed.). New York: Springer. ISBN 978-0-387-76501-3. 
  42. ↑ Latychevskaia, Tatiana; Woods, Colin Robert; Wang, Yi Bo; Holwill, Matthew; Prestat, Eric; Haigh, Sarah J.; Novoselov, Kostya S. (17 July 2018). "Convergent beam electron holography for analysis of van der Waals heterostructures". Proceedings of the National Academy of Sciences 115 (29): 7473–7478. doi:10.1073/pnas.1722523115. PMID 29970422. Bibcode: 2018PNAS..115.7473L. 




Retrieved from "https://handwiki.org/wiki/index.php?title=Convergent-beam_electron_diffraction&oldid=3369128"