Physics:Bragg's law

From HandWiki
Short description: Physical law regarding scattering angles of radiation through a medium

In many areas of science, Bragg's law, Wulff–Bragg's condition or Laue–Bragg interference, are a special case of Laue diffraction, giving the angles for coherent scattering of waves from a large crystal lattice. It describes how the superposition of wave fronts scattered by lattice planes leads to a strict relation between the wavelength and scattering angle. This law was initially formulated for X-rays, but it also applies to all types of matter waves including neutron and electron waves if there are a large number of atoms, as well as visible light with artificial periodic microscale lattices.

History

X-rays interact with the atoms in a crystal.
See also: X-ray crystallography#History

Bragg diffraction (also referred to as the Bragg formulation of X-ray diffraction) was first proposed by Lawrence Bragg and his father, William Henry Bragg, in 1913[1] after their discovery that crystalline solids produced surprising patterns of reflected X-rays (in contrast to those produced with, for instance, a liquid). They found that these crystals, at certain specific wavelengths and incident angles, produced intense peaks of reflected radiation.

According to the 2θ deviation, the phase shift causes constructive (left figure) or destructive (right figure) interferences.

Lawrence Bragg explained this result by modeling the crystal as a set of discrete parallel planes separated by a constant parameter d. He proposed that the incident X-ray radiation would produce a Bragg peak if reflections off the various planes interfered constructively. The interference is constructive when the phase difference between the wave reflected off different atomic planes is a multiple of 2π; this condition (see Bragg condition section below) was first presented by Lawrence Bragg on 11 November 1912 to the Cambridge Philosophical Society.[2] Although simple, Bragg's law confirmed the existence of real particles at the atomic scale, as well as providing a powerful new tool for studying crystals. Lawrence Bragg and his father, William Henry Bragg, were awarded the Nobel Prize in physics in 1915 for their work in determining crystal structures beginning with NaCl, ZnS, and diamond.[3] They are the only father-son team to jointly win.

The concept of Bragg diffraction applies equally to neutron diffraction[4] and approximately to electron diffraction.[5] In both cases the wavelengths are comparable with inter-atomic distances (~ 150 pm). Many other types of matter waves have also been shown to diffract,[6][7] and also light from objected with a larger ordered structure such as opals.[8]

Bragg condition

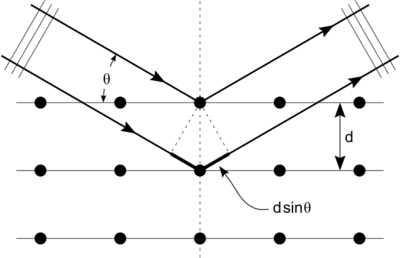
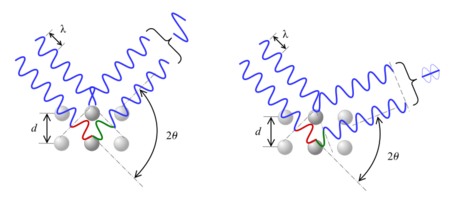
Bragg diffraction[9]:16 Two beams with identical wavelength and phase approach a crystalline solid and are scattered off two different atoms within it. The lower beam traverses an extra length of 2dsinθ. Constructive interference occurs when this length is equal to an integer multiple of the wavelength of the radiation.

Bragg diffraction occurs when radiation of a wavelength λ comparable to atomic spacings is scattered in a specular fashion (mirror-like reflection) by planes of atoms in a crystalline material, and undergoes constructive interference.[10] When the scattered waves are incident at a specific angle, they remain in phase and constructively interfere. The glancing angle θ (see figure on the right, and note that this differs from the convention in Snell's law where θ is measured from the surface normal), the wavelength λ, and the "grating constant" d of the crystal are connected by the relation:[11]:1026[math]\displaystyle{ n\lambda = 2 d\sin\theta }[/math]where [math]\displaystyle{ n }[/math] is the diffraction order ([math]\displaystyle{ n = 1 }[/math] is first order, [math]\displaystyle{ n = 2 }[/math] is second order,[10]:221 [math]\displaystyle{ n = 3 }[/math] is third order[11]:1028). This equation, Bragg's law, describes the condition on θ for constructive interference.[12]

A map of the intensities of the scattered waves as a function of their angle is called a diffraction pattern. Strong intensities known as Bragg peaks are obtained in the diffraction pattern when the scattering angles satisfy Bragg condition. This is a special case of the more general Laue equations, and the Laue equations can be shown to reduce to the Bragg condition with additional assumptions.[13]

Heuristic derivation

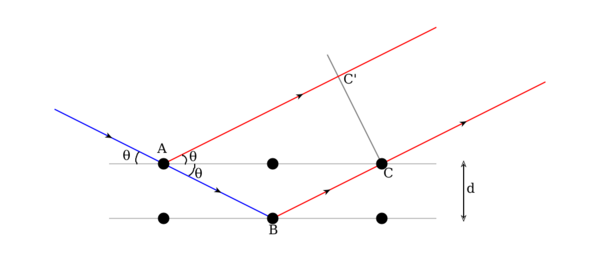
Suppose that a plane wave (of any type) is incident on planes of lattice points, with separation [math]\displaystyle{ d }[/math], at an angle [math]\displaystyle{ \theta }[/math] as shown in the Figure. Points A and C are on one plane, and B is on the plane below. Points ABCC' form a quadrilateral.

Bragg's law.svg

There will be a path difference between the ray that gets reflected along AC' and the ray that gets transmitted along AB, then reflected along BC. This path difference is [math]\displaystyle{ (AB + BC) - \left(AC'\right) \,. }[/math]

The two separate waves will arrive at a point (infinitely far from these lattice planes) with the same phase, and hence undergo constructive interference, if and only if this path difference is equal to any integer value of the wavelength, i.e. [math]\displaystyle{ n\lambda =(AB + BC) - \left(AC'\right) }[/math]

where [math]\displaystyle{ n }[/math] and [math]\displaystyle{ \lambda }[/math] are an integer and the wavelength of the incident wave respectively.

Therefore, from the geometry [math]\displaystyle{ AB = BC = \frac{d}{\sin\theta} \text{ and } AC = \frac{2d}{\tan\theta} \,, }[/math]

from which it follows that [math]\displaystyle{ AC' = AC\cdot\cos\theta = \frac{2d}{\tan\theta}\cos\theta = \left(\frac{2d}{\sin\theta}\cos\theta\right)\cos\theta = \frac{2d}{\sin\theta}\cos^2\theta \,. }[/math]

Putting everything together, [math]\displaystyle{ n\lambda = \frac{2d}{\sin\theta} - \frac{2d}{\sin\theta}\cos^2\theta = \frac{2d}{\sin\theta}\left(1 - \cos^2\theta\right) = \frac{2d}{\sin\theta}\sin^2\theta }[/math]

which simplifies to [math]\displaystyle{ n\lambda = 2d\sin\theta \,, }[/math] which is Bragg's law shown above.

If only two planes of atoms were diffracting, as shown in the Figure then the transition from constructive to destructive interference would be gradual as a function of angle, with gentle maxima at the Bragg angles. However, since many atomic planes are participating in most real materials, sharp peaks are typical.[5][13]

A rigorous derivation from the more general Laue equations is available (see page: Laue equations).

Beyond Bragg's law

See also: Electron diffraction
Typical selected area electron diffraction pattern. Each spot corresponds to a different diffracted direction.

The Bragg condition is correct for very large crystals. Because the scattering of X-rays and neutrons is relatively weak, in many cases quite large crystals with sizes of 100 nm or more are used. While there can be additional effects due to crystal defects, these are often quite small. In contrast, electrons interact thousands of times more strongly with solids than X-rays,[5] and also lose energy (inelastic scattering).[14] Therefore samples used in transmission electron diffraction are much thinner. Typical diffraction patterns, for instance the Figure, show spots for different directions (plane waves) of the electrons leaving a crystal. The angles that Bragg's law predicts are still approximately right, but in general there is a lattice of spots which are close to projections of the reciprocal lattice that is at right angles to the direction of the electron beam. (In contrast, Bragg's law predicts that only one or perhaps two would be present, not simultaneously tens to hundreds.) With low-energy electron diffraction where the electron energies are typically 30-1000 electron volts, the result is similar with the electrons reflected back from a surface.[15] Also similar is reflection high-energy electron diffraction which typically leads to rings of diffraction spots.[16]

With X-rays the effect of having small crystals is described by the Scherrer equation.[13][17][18] This leads to broadening of the Bragg peaks which can be used to estimate the size of the crystals.

Bragg scattering of visible light by colloids

A colloidal crystal is a highly ordered array of particles that forms over a long range (from a few millimeters to one centimeter in length); colloidal crystals have appearance and properties roughly analogous to their atomic or molecular counterparts.[8] It has been known for many years that, due to repulsive Coulombic interactions, electrically charged macromolecules in an aqueous environment can exhibit long-range crystal-like correlations, with interparticle separation distances often being considerably greater than the individual particle diameter. Periodic arrays of spherical particles give rise to interstitial voids (the spaces between the particles), which act as a natural diffraction grating for visible light waves, when the interstitial spacing is of the same order of magnitude as the incident lightwave.[19][20][21] In these cases brilliant iridescence (or play of colours) is attributed to the diffraction and constructive interference of visible lightwaves according to Bragg's law, in a matter analogous to the scattering of X-rays in crystalline solid. The effects occur at visible wavelengths because the interplanar spacing d is much larger than for true crystals. Precious opal is one example of a colloidal crystal with optical effects.

Volume Bragg gratings

Main page: Physics:Volume hologram

Volume Bragg gratings (VBG) or volume holographic gratings (VHG) consist of a volume where there is a periodic change in the refractive index. Depending on the orientation of the modulation of the refractive index, VBG can be used either to transmit or reflect a small bandwidth of wavelengths.[22] Bragg's law (adapted for volume hologram) dictates which wavelength will be diffracted:[23]

[math]\displaystyle{ 2\Lambda\sin(\theta + \varphi)=m\lambda_B \,, }[/math]

where m is the Bragg order (a positive integer), λB the diffracted wavelength, Λ the fringe spacing of the grating, θ the angle between the incident beam and the normal (N) of the entrance surface and φ the angle between the normal and the grating vector (KG). Radiation that does not match Bragg's law will pass through the VBG undiffracted. The output wavelength can be tuned over a few hundred nanometers by changing the incident angle (θ). VBG are being used to produce widely tunable laser source or perform global hyperspectral imagery (see Photon etc.).[23]

Selection rules and practical crystallography

Main page: Physics:X-ray crystallography

The measurement of the angles can be used to determine crystal structure, see x-ray crystallography for more details.[5][13] As a simple example, Bragg's law, as stated above, can be used to obtain the lattice spacing of a particular cubic system through the following relation:

[math]\displaystyle{ d = \frac{a}{\sqrt{h^2 + k^2 + \ell^2}} \,, }[/math]

where [math]\displaystyle{ a }[/math] is the lattice spacing of the cubic crystal, and h, k, and ℓ are the Miller indices of the Bragg plane. Combining this relation with Bragg's law gives:

[math]\displaystyle{ \left(\frac{\lambda}{2a}\right)^2 = \left(\frac{\lambda}{2d}\right)^2 \frac{1}{h^2 + k^2 + \ell^2} }[/math]

One can derive selection rules for the Miller indices for different cubic Bravais lattices as well as many others, a few of the selection rules are given in the table below.

Selection rules for the Miller indices
Bravais lattices Example compounds Allowed reflections Forbidden reflections
Simple cubic Po Any h, k, ℓ None
Body-centered cubic Fe, W, Ta, Cr h + k + ℓ = even h + k + ℓ = odd
Face-centered cubic (FCC) Cu, Al, Ni, NaCl, LiH, PbS h, k, ℓ all odd or all even h, k, ℓ mixed odd and even
Diamond FCC Si, Ge All odd, or all even with h + k + ℓ = 4n h, k, ℓ mixed odd and even, or all even with h + k + ℓ ≠ 4n
Triangular lattice Ti, Zr, Cd, Be ℓ even, h + 2k ≠ 3n h + 2k = 3n for odd ℓ

These selection rules can be used for any crystal with the given crystal structure. KCl has a face-centered cubic Bravais lattice. However, the K+ and the Cl− ion have the same number of electrons and are quite close in size, so that the diffraction pattern becomes essentially the same as for a simple cubic structure with half the lattice parameter. Selection rules for other structures can be referenced elsewhere, or derived. Lattice spacing for the other crystal systems can be found here.

See also

References

  1. ↑ Bragg, W. H.; Bragg, W. L. (1913). "The Reflexion of X-rays by Crystals". Proc. R. Soc. Lond. A 88 (605): 428–38. doi:10.1098/rspa.1913.0040. Bibcode: 1913RSPSA..88..428B. 
  2. ↑ There are some sources, like the Academic American Encyclopedia, that attribute the discovery of the law to both W.L Bragg and his father W.H. Bragg, but the official Nobel Prize site and the biographies written about him ("Light Is a Messenger: The Life and Science of William Lawrence Bragg", Graeme K. Hunter, 2004 and "Great Solid State Physicists of the 20th Century", Julio Antonio Gonzalo, Carmen Aragó López) make a clear statement that Lawrence Bragg alone derived the law.
  3. ↑ "The Nobel Prize in Physics 1915". https://www.nobelprize.org/prizes/physics/1915/summary/. 
  4. ↑ Shull, Clifford G. (1995). "Early development of neutron scattering". Reviews of Modern Physics 67 (4): 753–757. doi:10.1103/revmodphys.67.753. ISSN 0034-6861. http://dx.doi.org/10.1103/revmodphys.67.753. 
  5. ↑ 5.0 5.1 5.2 5.3 John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN:0-444-10791-6.
  6. ↑ Estermann, I.; Stern, O. (1930). "Beugung von Molekularstrahlen" (in de). Zeitschrift fur Physik 61 (1-2): 95–125. doi:10.1007/BF01340293. ISSN 1434-6001. http://link.springer.com/10.1007/BF01340293. 
  7. ↑ Arndt, Markus; Nairz, Olaf; Vos-Andreae, Julian; Keller, Claudia; van der Zouw, Gerbrand; Zeilinger, Anton (1999). "Wave–particle duality of C60 molecules" (in en). Nature 401 (6754): 680–682. doi:10.1038/44348. ISSN 0028-0836. https://www.nature.com/articles/44348. 
  8. ↑ 8.0 8.1 Pieranski, P (1983). "Colloidal Crystals". Contemporary Physics 24: 25–73. doi:10.1080/00107518308227471. Bibcode: 1983ConPh..24...25P. 
  9. ↑ Bragg, W. H.; Bragg, W. L. (1915). X Rays and Crystal Structure. G. Bell and Sons, Ltd. https://archive.org/details/xrayscrystalstru00braguoft/page/n5/mode/2up?ref=ol&view=theater. 
  10. ↑ 10.0 10.1 Moseley, Henry H. G. J.; Darwin, Charles G. (July 1913). "on the Reflexion of the X-rays". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 26 (151): 210–232. doi:10.1080/14786441308634968. https://scholar.archive.org/work/flhqgmpfrjfilkbsyj63usnhyu/access/ia_file/crossref-pre-1923-scholarly-works/10.1080%252F14786441108637173.zip/10.1080%252F14786441308634968.pdf. Retrieved 2021-04-27. 
  11. ↑ 11.0 11.1 Moseley, Henry G. J. (1913). Smithsonian Libraries. "The High-Frequency Spectra of the Elements". The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science. 6 (London-Edinburgh: London : Taylor & Francis) 26: 1024–1034. doi:10.1080/14786441308635052. https://archive.org/details/londonedinburg6261913lond/page/1024/mode/2up. 
  12. ↑ H. P. Myers (2002). Introductory Solid State Physics. Taylor & Francis. ISBN 0-7484-0660-3. 
  13. ↑ 13.0 13.1 13.2 13.3 Warren, Bertram Eugene (1990). X-ray diffraction. Dover books on physics and chemistry. New York: Dover. ISBN 978-0-486-66317-3. 
  14. ↑ Egerton, R. F. (2009). "Electron energy-loss spectroscopy in the TEM". Reports on Progress in Physics 72 (1): 016502. doi:10.1088/0034-4885/72/1/016502. Bibcode: 2009RPPh...72a6502E. 
  15. ↑ Moritz, Wolfgang; Van Hove, Michel (2022). Surface structure determination by LEED and X-rays. Cambridge, United Kingdom. ISBN 978-1-108-28457-8. OCLC 1293917727. https://www.worldcat.org/oclc/1293917727. 
  16. ↑ Ichimiya, Ayahiko; Cohen, Philip (2004). Reflection high-energy electron diffraction. Cambridge, U.K.: Cambridge University Press. ISBN 0-521-45373-9. OCLC 54529276. https://www.worldcat.org/oclc/54529276. 
  17. ↑ Scherrer, P. (1918). "Bestimmung der Größe und der inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1918: 98–100. https://eudml.org/doc/59018. 
  18. ↑ Patterson, A. L. (1939). "The Scherrer Formula for X-Ray Particle Size Determination". Physical Review 56 (10): 978–982. doi:10.1103/PhysRev.56.978. Bibcode: 1939PhRv...56..978P. https://link.aps.org/doi/10.1103/PhysRev.56.978. 
  19. ↑ Hiltner, PA; IM Krieger (1969). "Diffraction of Light by Ordered Suspensions". Journal of Physical Chemistry 73 (7): 2386–2389. doi:10.1021/j100727a049. 
  20. ↑ Aksay, IA (1984). "Microstructural Control through Colloidal Consolidation". Proceedings of the American Ceramic Society 9: 94. 
  21. ↑ Luck, Werner; Klier, Manfred; Wesslau, Hermann (1963). "Über Bragg-Reflexe mit sichtbarem Licht an monodispersen Kunststofflatices. II". Berichte der Bunsengesellschaft für physikalische Chemie 67 (1): 84–85. doi:10.1002/bbpc.19630670114. ISSN 0005-9021. 
  22. ↑ Barden, S.C.; Williams, J.B.; Arns, J.A.; Colburn, W.S. (2000). "Tunable Gratings: Imaging the Universe in 3-D with Volume-Phase Holographic Gratings (Review)". ASP Conf. Ser. 195: 552. Bibcode: 2000ASPC..195..552B. https://ui.adsabs.harvard.edu/link_gateway/2000ASPC..195..552B/ADS_PDF. 
  23. ↑ 23.0 23.1 C. Kress, Bernard; Meyruels, Patrick (2009). Applied Digital Optics : From Micro-optics to Nanophotonics. Wiley. pp. Chpt 8. ISBN 978-0-470-02263-4. https://download.e-bookshelf.de/download/0000/5677/23/L-G-0000567723-0002356955.pdf. 

Further reading

  • Neil W. Ashcroft and N. David Mermin, Solid State Physics (Harcourt: Orlando, 1976).
  • Bragg, W.L. (1913). "The Diffraction of Short Electromagnetic Waves by a Crystal". Proceedings of the Cambridge Philosophical Society 17: 43–57. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Bragg%27s_law&oldid=3277007"