Critical graph

Short description: Undirected graph

On the left-top a vertex critical graph with chromatic number 6; next all the N-1 subgraphs with chromatic number 5.

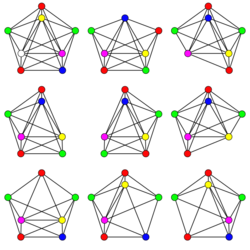
In graph theory, a critical graph is an undirected graph all of whose proper subgraphs have smaller chromatic number. In such a graph, every vertex or edge is a critical element, in the sense that its deletion would decrease the number of colors needed in a graph coloring of the given graph. The decrease in the number of colors cannot be by more than one.

Variations

A [math]\displaystyle{ k }[/math]-critical graph is a critical graph with chromatic number [math]\displaystyle{ k }[/math]. A graph [math]\displaystyle{ G }[/math] with chromatic number [math]\displaystyle{ k }[/math] is [math]\displaystyle{ k }[/math]-vertex-critical if each of its vertices is a critical element. Critical graphs are the minimal members in terms of chromatic number, which is a very important measure in graph theory.

Some properties of a [math]\displaystyle{ k }[/math]-critical graph [math]\displaystyle{ G }[/math] with [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ m }[/math] edges:

• [math]\displaystyle{ G }[/math] has only one component.
• [math]\displaystyle{ G }[/math] is finite (this is the de Bruijn–Erdős theorem).
• The minimum degree [math]\displaystyle{ \delta(G) }[/math] obeys the inequality [math]\displaystyle{ \delta(G)\ge k-1 }[/math]. That is, every vertex is adjacent to at least [math]\displaystyle{ k-1 }[/math] others. More strongly, [math]\displaystyle{ G }[/math] is [math]\displaystyle{ (k-1) }[/math]-edge-connected.
• If [math]\displaystyle{ G }[/math] is a regular graph with degree [math]\displaystyle{ k-1 }[/math], meaning every vertex is adjacent to exactly [math]\displaystyle{ k-1 }[/math] others, then [math]\displaystyle{ G }[/math] is either the complete graph [math]\displaystyle{ K_k }[/math] with [math]\displaystyle{ n=k }[/math] vertices, or an odd-length cycle graph. This is Brooks' theorem.
• [math]\displaystyle{ 2m\ge(k-1)n+k-3 }[/math].
• [math]\displaystyle{ 2m\ge (k-1)n+\lfloor(k-3)/(k^2-3)\rfloor n }[/math].
• Either [math]\displaystyle{ G }[/math] may be decomposed into two smaller critical graphs, with an edge between every pair of vertices that includes one vertex from each of the two subgraphs, or [math]\displaystyle{ G }[/math] has at least [math]\displaystyle{ 2k-1 }[/math] vertices. More strongly, either [math]\displaystyle{ G }[/math] has a decomposition of this type, or for every vertex [math]\displaystyle{ v }[/math] of [math]\displaystyle{ G }[/math] there is a [math]\displaystyle{ k }[/math]-coloring in which [math]\displaystyle{ v }[/math] is the only vertex of its color and every other color class has at least two vertices.

Graph [math]\displaystyle{ G }[/math] is vertex-critical if and only if for every vertex [math]\displaystyle{ v }[/math], there is an optimal proper coloring in which [math]\displaystyle{ v }[/math] is a singleton color class.

As (Hajós 1961) showed, every [math]\displaystyle{ k }[/math]-critical graph may be formed from a complete graph [math]\displaystyle{ K_k }[/math] by combining the Hajós construction with an operation that identifies two non-adjacent vertices. The graphs formed in this way always require [math]\displaystyle{ k }[/math] colors in any proper coloring.

A double-critical graph is a connected graph in which the deletion of any pair of adjacent vertices decreases the chromatic number by two. It is an open problem to determine whether [math]\displaystyle{ K_k }[/math] is the only double-critical [math]\displaystyle{ k }[/math]-chromatic graph.

See also

• Factor-critical graph

Further reading

• Jensen, T. R.; Toft, B. (1995), Graph coloring problems, New York: Wiley-Interscience, ISBN 0-471-02865-7 
• Stiebitz, Michael; Tuza, Zsolt; Voigt, Margit (6 August 2009), "On list critical graphs", Discrete Mathematics (Elsevier) 309 (15): 4931–4941, doi:10.1016/j.disc.2008.05.021