Crossed ladders problem

Short description: Mathematical puzzle

The crossed ladders problem is a puzzle of unknown origin that has appeared in various publications and regularly reappears in Web pages and Usenet discussions.

The problem

Crossed ladders of lengths a and b. h is half the harmonic mean of A and B; equivalently, the reciprocals of A and B sum to the reciprocal of h (the optic equation). Given a, b, and h, find w.

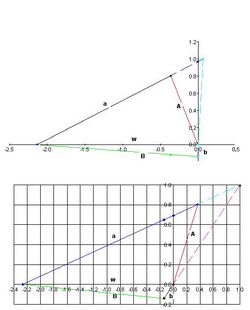
Two ladders of lengths a and b lie oppositely across an alley, as shown in the figure. The ladders cross at a height of h above the alley floor. What is the width of the alley?

Martin Gardner presents and discusses the problem in his book of mathematical puzzles published in 1979 and cites references to it as early as 1895. The crossed ladders problem may appear in various forms, with variations in name, using various lengths and heights, or requesting unusual solutions such as cases where all values are integers. Its charm has been attributed to a seeming simplicity which can quickly devolve into an "algebraic mess" (characterization attributed by Gardner to D. F. Church).

Solution

The problem description implies that w > 0, that a > w, and b > w, that h > 0, and that A > h, B > h, where A and B are the heights of the walls where sides of lengths b and a respectively lean (as in the above graph).

Both solution methods below rely on the property that A, B, and H satisfy the optic equation, i.e. [math]\displaystyle{ \tfrac{1}{A} + \tfrac{1}{B} = \tfrac{1}{h}, }[/math], which can be seen as follows:

Divide the baseline into two parts at the point where it meets [math]\displaystyle{ h }[/math], and call the left and right parts [math]\displaystyle{ w_1 }[/math] and [math]\displaystyle{ w_2 }[/math] respectively. The angle where [math]\displaystyle{ a }[/math] meets [math]\displaystyle{ w }[/math] is common to two similar triangles with bases [math]\displaystyle{ w }[/math] and [math]\displaystyle{ w_1 }[/math] respectively. The angle where [math]\displaystyle{ b }[/math] meets [math]\displaystyle{ w }[/math] is common to two similar triangles with bases [math]\displaystyle{ w }[/math] and [math]\displaystyle{ w_2 }[/math] respectively. This tells us that

[math]\displaystyle{ \frac{B}{w} = \frac{h}{w_1} \quad \text{and} \quad \frac{A}{w} = \frac{h}{w_2}, \quad \text{where} \quad w_1 \gt 0, w_2 \gt 0, }[/math]

which we can then re-arrange (using [math]\displaystyle{ w_1 + w_2 = w }[/math]) to get

[math]\displaystyle{ \frac{1}{A} + \frac{1}{B} = \frac{1}{h}. }[/math]

First method

Two statements of the Pythagorean theorem (see figure above)

[math]\displaystyle{ A^2 + w^2 = b^2 }[/math]

and

[math]\displaystyle{ B^2 + w^2 = a^2 }[/math]

can be subtracted one from the other to eliminate w, and the result can be combined with [math]\displaystyle{ \tfrac{1}{A} + \tfrac{1}{B} = \tfrac{1}{h} }[/math] with alternately A or B solved out to yield the quartic equations

[math]\displaystyle{ A^4 - 2hA^3 + (h - A)^2 (a^2 - b^2) = 0, }[/math]

[math]\displaystyle{ B^4 - 2hB^3 + (h - B)^2 (b^2 - a^2) = 0. }[/math]

These can be solved algebraically or numerically for the wall heights A and B, and the Pythagorean theorem on one of the triangles can be used to solve for the width w.

Second method

The problem may be reduced to the quartic equation x³(x − c) − 1 = 0, which can be solved by approximation methods, as suggested by Gardner, or the quartic may be solved in closed form by Ferrari's method. Once x is obtained, the width of the alley is readily calculated. A derivation of the quartic is given below, along with the desired width in terms of the quartic solution. Note that the requested unknown w does not appear directly in most of the derivation.

From [math]\displaystyle{ \tfrac{1}{A} + \tfrac{1}{B} = \tfrac{1}{h}, }[/math] we get

[math]\displaystyle{ \text{(Eq. 1)} \quad A B = h (A + B). }[/math]

Using the Pythagorean theorem, we can see that

[math]\displaystyle{ w^2 + B^2 = a^2 }[/math] and [math]\displaystyle{ w^2 + A^2 = b^2. }[/math]

By isolating [math]\displaystyle{ w^2 }[/math] on both equations, we see that

[math]\displaystyle{ a^2 - B^2 = b^2 - A^2, }[/math]

which can be rearranged and factored into

[math]\displaystyle{ \text{(Eq. 2)} \quad a^2 - b^2 = (B + A) (B - A). }[/math]

Square (Eq. 2) and combine with (Eq. 1):

[math]\displaystyle{ (a^2 - b^2)^2 = (B + A)^2 (B - A)^2, }[/math]

[math]\displaystyle{ (a^2 - b^2)^2 = (B + A)^2 (B^2 - 2AB + A^2). }[/math]

Rearrange to get

[math]\displaystyle{ (a^2 - b^2)^2 = (A + B)^2 (A^2 + B^2 - 2AB). }[/math]

Then

[math]\displaystyle{ (a^2 - b^2)^2 = (A + B)^2 (A^2 + B^2 + 2AB - 4AB), }[/math]

[math]\displaystyle{ (a^2 - b^2)^2 = (A + B)^2 \big((A^2 + 2AB + B^2) - 4AB\big), }[/math]

[math]\displaystyle{ (a^2 - b^2)^2 = (A + B)^2 \big((A + B)^2 - 4AB\big). }[/math]

Now, combine with (Eq. 1):

[math]\displaystyle{ (a^2 - b^2)^2 = (A + B)^2 \big((A + B)^2 - 4h(A + B)\big), }[/math]

[math]\displaystyle{ (a^2 - b^2)^2 = (A + B)^2 (A + B)\big((A + B) - 4h\big). }[/math]

Finally,

[math]\displaystyle{ \text{(Eq. 3)} \quad (a^2 - b^2)^2 = (A + B)^3 (A + B - 4h). }[/math]

Let

[math]\displaystyle{ x = \frac{A + B}{\sqrt{a^2 - b^2}}, }[/math]

[math]\displaystyle{ c = \frac{4 h}{\sqrt{a^2-b^2}}. }[/math]

Then

[math]\displaystyle{ x^3(x - c) - 1 = 0. }[/math] (same as Eq. 3 with the sides reversed)

The above fourth-power equation can be solved for x using any available method. The width of the alley is then found by using the value found for x: The identity

[math]\displaystyle{ A + B = A + \sqrt{A^2 + (a^2 - b^2)} }[/math]

can be used to find A, and w can finally be found by

[math]\displaystyle{ w = \sqrt{b^2 - A^2}. }[/math]

A quartic equation has four solutions, and only one solution for this equation matches the problem as presented. Another solution is for a case where one ladder (and wall) is below ground level and the other above ground level. In this case the ladders do not actually cross, but their extensions do so at the specified height. The other two solutions are a pair of conjugate complex numbers. The equation does not have the ladder lengths explicitly defined, only the difference of their squares, so one could take the length as any value that makes them cross, and the wall spacing would be defined as between where the ladders intersect the walls.

As the wall separation approaches zero, the height of the crossing approaches [math]\displaystyle{ h = \frac{ab}{a + b}. }[/math] This is because [math]\displaystyle{ \tfrac{1}{A} + \tfrac{1}{B} = \tfrac{1}{h} }[/math] (proven at the start) implies [math]\displaystyle{ h = \tfrac{AB}{A + B}, }[/math] and as w goes to zero, b goes to A and a goes to B according to the top diagram.

As the solutions to the equation involve square roots, negative roots are equally valid. They can be interpreted as both ladders and walls being below ground level and with them in opposing sense, they can be interchanged.

The complex solutions can be interpreted as wall A leaning to the left or right and wall B below ground, so the intersection is between extensions to the ladders as shown for the case a, b, h = 3, 2, 1. The ladders a and b and [math]\displaystyle{ a^2 - b^2 }[/math] are not as specified. The base w is a function of A, B, and h, and the complex values of A and B can be found from the alternative quartic

[math]\displaystyle{ x^4 - 2 h x^3 + D x^2 - 2 h D x + h^2 D = 0 }[/math]

with D being [math]\displaystyle{ a^2 - b^2 }[/math] for one wall and [math]\displaystyle{ b^2 - a^2 }[/math] for the other (±5 in the example). Note that the imaginary solutions are horizontal and the real ones are vertical. The value D is found in the solution as the real part of the difference in the squares of the complex coordinates of the two walls. The imaginary part = 2X_aY_a = 2X_bY_b (walls a and b). The short ladder in the complex solution in the 3, 2, 1 case appears to be tilted at 45 degrees, but actually slightly less with a tangent of 0.993. Other combinations of ladder lengths and crossover height have comparable complex solutions. With combination 105, 87, 35 the short ladder tangent is approximately 0.75.

Integer solutions

There are solutions in which all parameters are integers. For example, (a, b, A, B, w₁, w₂, w, h) = (119, 70, 42, 105, 16, 40, 56, 30). Such solutions involve Pythagorean triples for the two right triangles with sides (A, w, b) and (B, w, a) and integer solutions of the optic equation [math]\displaystyle{ \tfrac{1}{A}+\tfrac{1}{B}=\tfrac{1}{h}. }[/math]

Application to paper folding

Folding a rectangular sheet of paper into thirds using the crossed ladders problem

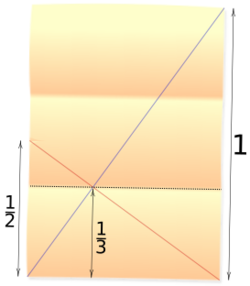
The optic equation of the crossed ladders problem can be applied to folding rectangular paper into three equal parts:

1/1/2 + 1/1 = 1/h   ∴   2 + 1 = 1/h   ∴   h = 1/2 + 1 = 1/3

One side (left in the illustration) is partially folded in half and pinched to leave a mark. The intersection of a line from this mark to an opposite corner (red) with a diagonal (blue) is exactly one third from the bottom edge. The top edge can then be folded down to meet the intersection.

It is also exactly one third horizontally from the left edge; folding the right edge to meet the intersection lets the paper be folded into thirds lengthwise.

Similarly, folding the left side twice to get quarters lets one fold the sheet into five equal parts:

1/1/4 + 1/1 = 1/h′   ∴   4 + 1 = 1/h′   ∴   h′ = 1/4 + 1 = 1/5

and folding it thrice to get eights lets one fold the sheet into nine equal parts, etc.:

1/1/8 + 1/1 = 1/h″   ∴   8 + 1 = 1/h″   ∴   h″ = 1/8 + 1 = 1/9

Extended crossed ladders theorem

The crossed ladders theorem was extended to crossed ladders within a triangle. In 2002, Harold Joseph Stengel (1947–2007), an American secondary school teacher of mathematics, proved the extended theorem.

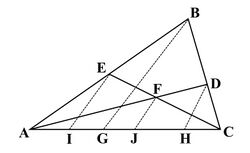
Let AC be the base of a triangle ABC. Let ladder (line) AD have its foot at A and intersect BC at D; likewise, let ladder CE have its foot at C and intersect AB at E. Let AD intersect CE at F. Extend parallel lines from the points E, B, F, and D, intersecting AC at the points I, G, J, and H, respectively. Then

1/EI + 1/DH = 1/FJ + 1/BG

whence it follows that

1/area (△ AEC) + 1/area (△ ADC) = 1/area (△ AFC) + 1/area (△ ABC).

See also

• Right trapezoid, the quadrilateral with vertices at the tops and bottoms of the two ladders

External links

• Crossed Ladders Theorem by Jay Warendorff, the Wolfram Demonstrations Project.
• Solving the crossing ladders puzzle (with Python, GNU GSL, Octave, Maxima and Sage).