Cubinder
In four-dimensional geometry, the cubinder (otherwise known as cubical cylinder or hypercylinder) is one way to generalise the 3D cylinder to 4D. Like the duocylinder and spherinder, it is also analogous to a cylinder in 3-space, which is the Cartesian product of a disk with a line segment.
- [math]\displaystyle{ D = \{(x,y,z,w) \mid x^2 + y^2 = 1, |z| = 1, |w| = 1 \} }[/math][1]
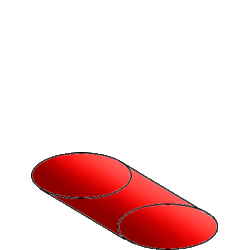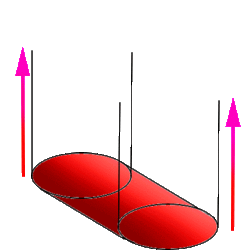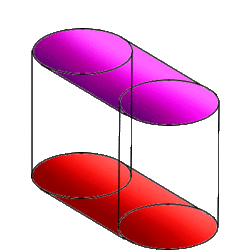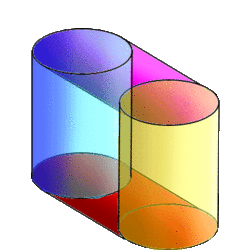
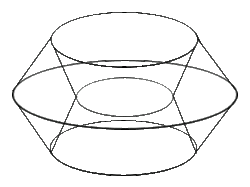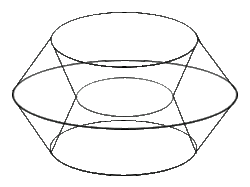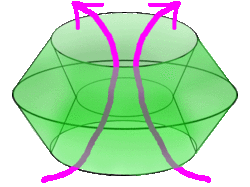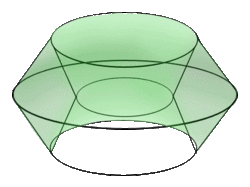
The Cubinder is the Cartesian Product of a circle and a square, and it is a rotachoron. It can be constructed by extrusion of a 3D cylinder along the W- axis by a unit distance.[2] The net of a cubinder is given by a single cube, surrounded by 4 cylinders.
Geometry
Formulae
- [math]\displaystyle{ \text{volume} = 2\pi rh(h+2r) }[/math]
- [math]\displaystyle{ \text{bulk} = \pi r^2h^2 }[/math][3]
Subfacets
| Tera (4D) | 1 cubinder |
|---|---|
| Cells (3D) | 4 cylinders and 1 cell bounded by a square torus[citation needed] |
| Faces (2D) | 4 discs and 4 tubes |
| Edges (1D) | 4 circles |
| Vertices (0D) | none |
Rolling
The square torus that binds the cubinder forms a circular surface on which the cubinder can roll. Like a circle and a cylinder, it can only roll the space of a line. The cubinder cannot roll on the 4 cylinders, as they are flat in 4D.[4]
Projection
The diagram is a perspective projection of the cubinder. The cubinder is rotated 45 degrees in the ZW plane. This allows us to observe that the cubinder is made up of four cylinders. However the square torus joining the cylinders cannot be observed from this perspective.
Relationship to other shapes
In 4-space, there are three intermediate forms between the tesseract (1 ball × 1 ball × 1 ball × 1 ball) and the hypersphere (4-ball). These are as follows:
- cubinder (2-ball × 1-ball × 1-ball)
- spherinder (3-ball × 1-ball)
- duocylinder (2-ball × 2-ball).
The cubinder is also a rotatope (more specifically a rotachoron), along with other shapes such as the tesseract, duocylinder, spherinder, and glome. A rotachoron is a four dimensional shape which can by formed by extensions and rotations.[5] The cubinder is a rotachoron as it can be formed via extension of a cylinder or rotation of a cube.
| Dimension | n-type | n-cube | m-sphere
crosses |
n-sphere | n-ball |
|---|---|---|---|---|---|
| 2nd | rotagon | square | circle | disk | |
| 3rd | rotahedron | cube | cylinder | sphere | ball |
| 4th | rotachoron | tesseract | cubinder,
spherinder |
glome | gongyl |
The rotation of cubinder to 5D is non-unique: rotating it around a cubic cross-section will lead to the shape, spherisquare. However, if you rotate it around its cylindrical cross-section, you will get a different rotatope called "dual cylinder", which can be also gotten by extending the duocylinder.[7]
See also
References
- ↑ Chandra, Satapathy Suresh; Biswal, Bhabendra Narayan; Udgata, Siba K.; Mandal, J. K. (2014-10-31) (in en). Proceedings of the 3rd International Conference on Frontiers of Intelligent Computing: Theory and Applications (FICTA) 2014. Springer. ISBN 9783319120126. https://books.google.ie/books?id=cb4hBQAAQBAJ&pg=PA504&lpg=PA504&dq=cubinder&source=bl&ots=wqUa_cxJus&sig=rmy2IIMcIfVNa3V1x0je5R1iTQE&hl=en&sa=X&ved=0ahUKEwiig4XsmNHRAhWJOsAKHaeLA4wQ6AEIUzAO#v=onepage&q=cubinder&f=false.
- ↑ Banerjee, Agnijo. "Four dimensional space". http://www.agnijomaths.com/categories/geometry/Euclidean_geometry/four_dimensional_space.html.
- ↑ "Rotachora". http://hi.gher.space/classic/shapes/rotachora.htm.
- ↑ "The Cubical Cylinder" (in en). http://eusebeia.dyndns.org/4d/cubinder.
- ↑ "Appendix:List of protologisms/Q–Z – Wiktionary" (in en). https://en.wiktionary.org/wiki/Appendix:List_of_protologisms/Q%E2%80%93Z#rotatope.
- ↑ "Fourth Dimension Glossary". http://hi.gher.space/classic/glossary.htm.
- ↑ "Hi.gher. Space • View topic – Disagreement with the Duocylinder" (in en-gb). http://hi.gher.space/forum/viewtopic.php?f=24&t=409&start=0.