DSatur

Short description: Graph colouring algorithm by Daniel Brélaz

DSatur

Class	Graph coloring
Worst-case space complexity	Ο(n2)

DSatur is a graph colouring algorithm put forward by Daniel Brélaz in 1979. Similarly to the greedy colouring algorithm, DSatur colours the vertices of a graph one after another, adding a previously unused colour when needed. Once a new vertex has been coloured, the algorithm determines which of the remaining uncoloured vertices has the highest number of colours in its neighbourhood and colours this vertex next. Brélaz defines this number as the degree of saturation of a given vertex. The contraction of the term "degree of saturation" forms the name of the algorithm. DSatur is a heuristic graph colouring algorithm, yet produces exact results for bipartite, cycle, and wheel graphs. DSatur has also been referred to as saturation LF in the literature.

Pseudocode

Let the "degree of saturation" of a vertex be the number of different colours being used by its neighbors. Given a simple, undirected graph [math]\displaystyle{ G }[/math] compromising a vertex set [math]\displaystyle{ V }[/math] and edge set [math]\displaystyle{ E }[/math], the algorithm assigns colors to all of the vertices using color labels [math]\displaystyle{ 1,2,3,... }[/math]. The algorithm operates as follows:

1. Let [math]\displaystyle{ v }[/math] be the uncolored vertex in [math]\displaystyle{ G }[/math] with the highest degree of saturation. In cases of ties, choose the vertex among these with the largest degree in the subgraph induced by the uncolored vertices.
2. Assign [math]\displaystyle{ v }[/math] to the lowest color label not being used by any of its neighbors.
3. If all vertices have been colored, then end; otherwise return to Step 1.

Step 2 of this algorithm assigns colors to vertices using the same scheme as the greedy colouring algorithm. The main differences between the two approaches arises in Step 1 above, where vertices seen to be the most "constrained" are coloured first.

Example

Wheel graph with seven vertices and twelve edges

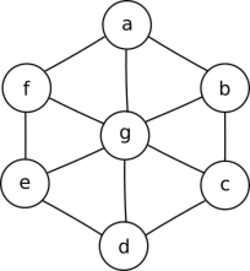
Consider the graph [math]\displaystyle{ G=(V,E) }[/math] shown on the right. This is a wheel graph and will therefore be optimally colored by the DSatur algorithm. Executing the algorithm results in the vertices being selected and colored as follows. (In this example, where ties occur in both of DSatur's heuristics, the vertex with lowest lexicographic labelling among these is chosen.)

1. Vertex [math]\displaystyle{ g }[/math] (color 1)
2. Vertex [math]\displaystyle{ a }[/math] (color 2)
3. Vertex [math]\displaystyle{ b }[/math] (color 3)
4. Vertex [math]\displaystyle{ c }[/math] (color 2)
5. Vertex [math]\displaystyle{ d }[/math] (color 3)
6. Vertex [math]\displaystyle{ e }[/math] (color 2)
7. Vertex [math]\displaystyle{ f }[/math] (color 3)

This gives the final three-colored solution [math]\displaystyle{ \mathcal{S} = \{\{g\}, \{a, c, e\}, \{b, d, f\}\} }[/math].

Performance

The worst-case complexity of DSatur is [math]\displaystyle{ O(n^2) }[/math], where [math]\displaystyle{ n }[/math] is the number of vertices in the graph. This is because the process of selecting the next vertex to colour takes [math]\displaystyle{ O(n) }[/math] time, and this process is carried out [math]\displaystyle{ n }[/math] times. The algorithm can also be implemented using a binary heap to store saturation degrees, operating in [math]\displaystyle{ O((n+m)\log n) }[/math], or [math]\displaystyle{ O(m+n\log n) }[/math] using Fibonacci heap, where [math]\displaystyle{ m }[/math] is the number of edges in the graph. This produces much faster runs with sparse graphs.

DSatur is known to be exact for bipartite graphs, as well as for cycle and wheel graphs. In an empirical comparison by Lewis in 2021, DSatur produced significantly better vertex colourings than the greedy algorithm on random graphs with edge probability [math]\displaystyle{ p=0.5 }[/math], while in turn producing significantly worse colourings than the recursive largest first algorithm.

External links

• High-Performance Graph Colouring Algorithms Suite of graph colouring algorithms (implemented in C++) used in the book A Guide to Graph Colouring: Algorithms and Applications (Springer International Publishers, 2021).
• C++ implementation of the DSatur Algorithm, presented as part of the article The DSatur Algorithm for Graph Coloring, Geeks for Geeks (2021)