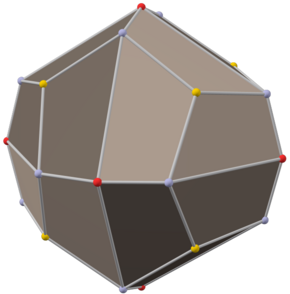
Dyakis dodecahedron
| Dyakis dodecahedron | |
|---|---|
 (rotating and 3D model) | |
| Type | Non-uniform |
| Face polygon | Chiral quadrilateral with 2 unequal acute angles & 2 unequal obtuse angles |
| Faces | 24, congruent |
| Edges | 48 |
| Vertices | 26 |
| Face configuration | V3.4.4.4 |
| Symmetry group | Pyritohedral |
| Dual polyhedron | Cantic snub octahedron |
| Properties | convex, face-transitive |
| |
In geometry, the dyakis dodecahedron or diploid is a variant of the deltoidal icositetrahedron with pyritohedral symmetry, transforming the kite faces into chiral quadrilaterals. It is the dual of the cantic snub octahedron. It can be constructed by enlarging 24 of the 48 faces of the disdyakis dodecahedron, and is inscribed in the dyakis dodecahedron,[1] which exists as a hemihedral form of it with indices {hkl}.[2] It can be constructed into two non regular pentagonal dodecahedra, the pyritohedron and the tetartoid. The transformation to the pyritohedron can be made by combining two adjacent trapezoids that share a long edge together into one hexagon face, which is a pyritohedral pentagon with an extra vertex added. The edges that bend at it can be combined and the vertex removed to finally get the pentagon. The transformation to the tetartoid can be made by enlarging 12 of the dyakis dodecahedron's 24 faces.
Since the quadrilaterals are chiral and non-regular, the dyakis dodecahedron is a non-uniform polyhedron, a type of polyhedron that isn't vertex transitive and doesn't have regular polygon faces. Since it is face-transitive, it is an isohedron.[3] The name diploid derives from the Greek word διπλάσιος (diplásios), meaning twofold since it has 2-fold symmetry along its 6 octahedral vertices. It has the same number of faces, edges and vertices as the deltoidal icositetrahedron as they are topologically identical.
In crystallography
In crystallography, the dyakis dodecahedron only exists in one crystal, which is pyrite. Pyrite has other forms other than the dyakis dodecahedron, including tetrahedra, octahedra, cubes and pyritohedra. Though the cube and octahedron are in the cubic crystal system, the dyakis dodecahedron and the pyritohedon are in the isometric crystal system and the tetrahedron is in the tetrahedral crystal system. Though the dyakis dodecahedron has 3-fold axes like the pyritohedron and cube, it doesn't have 4-fold axes but it does have order-4 vertices, as when the dyakis dodecahedron is rotated 90 or 270° along an order-4 vertex, it is not the same as before, because the order-4 vertices act as 2-fold axes, as when they are rotated a full turn or 180°, the polyhedron looks the same as before.
References
- ↑ Wadsworth, Marshman Edward (1909) (in en). Crystallography: An Elementary Manual for the Laboratory. J.J. McVey. https://books.google.co.uk/books?id=GyQ-AAAAIAAJ&pg=PA246&lpg=PA246&dq=%22dyakis+dodecahedron%22&source=bl&ots=hnIi6qCBRh&sig=ACfU3U0OumyNVsx_svWtDy_htNMfUabbKA&hl=en&sa=X&redir_esc=y#v=onepage&q=dyakis&f=false.
- ↑ Spencer, Leonard James (1911). "Crystallography". Encyclopædia Britannica. 7 (11th ed.). pp. 569-591.
- ↑ 24q Isohedra
 |
