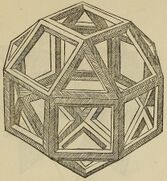
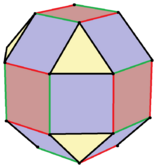
Rhombicuboctahedron

Short description: Archimedean solid with 26 faces

Rhombicuboctahedron
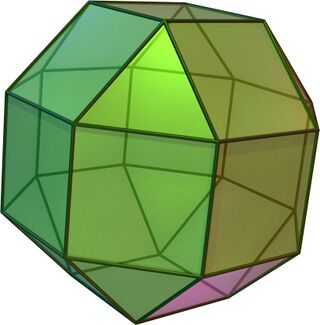(Click here for rotating model)
Type	Archimedean solid Uniform polyhedron
Elements	F = 26, E = 48, V = 24 (χ = 2)
Faces by sides	8{3}+(6+12){4}
Conway notation	eC or aaC aaaT
Schläfli symbols	rr{4,3} or [math]\displaystyle{ r\begin{Bmatrix} 4 \\ 3 \end{Bmatrix} }[/math]
	t0,2{4,3}
Wythoff symbol	3 4 | 2
Coxeter diagram
Symmetry group	Oh, B3, [4,3], (*432), order 48
Rotation group	O, [4,3]+, (432), order 24
Dihedral angle	3-4: 144°44′08″ (144.74°) 4-4: 135°
References	U10, C22, W13
Properties	Semiregular convex
Colored faces	3.4.4.4 (Vertex figure)
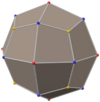Deltoidal icositetrahedron (dual polyhedron)	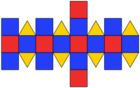Net

In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is a polyhedron with eight triangular, six square, and twelve rectangular faces. There are 24 identical vertices, with one triangle, one square, and two rectangles meeting at each one. If all the rectangles are themselves square (equivalently, all the edges are the same length, ensuring the triangles are equilateral), it is an Archimedean solid. The polyhedron has octahedral symmetry, like the cube and octahedron. Its dual is called the deltoidal icositetrahedron or trapezoidal icositetrahedron, although its faces are not really true trapezoids.

Names

Johannes Kepler in Harmonices Mundi (1618) named this polyhedron a rhombicuboctahedron, being short for truncated cuboctahedral rhombus, with cuboctahedral rhombus being his name for a rhombic dodecahedron. There are different truncations of a rhombic dodecahedron into a topological rhombicuboctahedron: Prominently its rectification (left), the one that creates the uniform solid (center), and the rectification of the dual cuboctahedron (right), which is the core of the dual compound.

It can also be called an expanded or cantellated cube or octahedron, from truncation operations on either uniform polyhedron.

Geometric relations

The rhombicuboctahedron can be seen as either an expanded cube (the blue faces) or an expanded octahedron (the red faces).

There are distortions of the rhombicuboctahedron that, while some of the faces are not regular polygons, are still vertex-uniform. Some of these can be made by taking a cube or octahedron and cutting off the edges, then trimming the corners, so the resulting polyhedron has six square and twelve rectangular faces. These have octahedral symmetry and form a continuous series between the cube and the octahedron, analogous to the distortions of the rhombicosidodecahedron or the tetrahedral distortions of the cuboctahedron. However, the rhombicuboctahedron also has a second set of distortions with six rectangular and sixteen trapezoidal faces, which do not have octahedral symmetry but rather T_h symmetry, so they are invariant under the same rotations as the tetrahedron but different reflections.

The lines along which a Rubik's Cube can be turned are, projected onto a sphere, similar, topologically identical, to a rhombicuboctahedron's edges. In fact, variants using the Rubik's Cube mechanism have been produced which closely resemble the rhombicuboctahedron.

The rhombicuboctahedron is used in three uniform space-filling tessellations: the cantellated cubic honeycomb, the runcitruncated cubic honeycomb, and the runcinated alternated cubic honeycomb.

Dissection

The rhombicuboctahedron can be dissected into two square cupolae and a central octagonal prism. A rotation of one cupola by 45 degrees creates the pseudo­rhombi­cubocta­hedron. Both of these polyhedra have the same vertex figure: 3.4.4.4.

The triangles are staggered in a pseudo­rhombi­cubocta­hedron (top) but aligned in a rhombi­cubocta­hedron (bottom)

There are three pairs of parallel planes that each intersect the rhombicuboctahedron in a regular octagon. The rhombicuboctahedron may be divided along any of these to obtain an octagonal prism with regular faces and two additional polyhedra called square cupolae, which count among the Johnson solids; it is thus an elongated square orthobicupola. These pieces can be reassembled to give a new solid called the elongated square gyrobicupola or pseudorhombicuboctahedron, with the symmetry of a square antiprism. In this the vertices are all locally the same as those of a rhombicuboctahedron, with one triangle and three squares meeting at each one, but are not all identical with respect to the entire polyhedron, since some are closer to the symmetry axis than others.

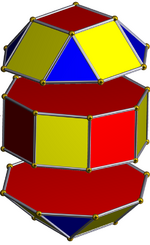
	Rhombicuboctahedron
	Pseudorhombicuboctahedron

Orthogonal projections

The rhombicuboctahedron has six special orthogonal projections, centered, on a vertex, on two types of edges, and three types of faces: triangles, and two squares. The last two correspond to the B₂ and A₂ Coxeter planes.

Orthogonal projections

Centered by	Vertex	Edge 3-4	Edge 4-4	Face Square-1	Face Square-2	Face Triangle
Solid
Wireframe
Projective symmetry	[2]	[2]	[2]	[2]	[4]	[6]
Dual

Spherical tiling

The rhombicuboctahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

	(6) square-centered	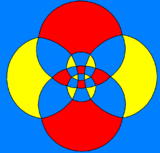(6) square-centered	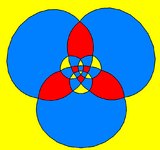(8) triangle-centered
Orthogonal projection	Stereographic projections

Pyritohedral symmetry

A half symmetry form of the rhombicuboctahedron, , exists with pyritohedral symmetry, [4,3⁺], (3*2) as Coxeter diagram , Schläfli symbol s₂{3,4}, and can be called a cantic snub octahedron. This form can be visualized by alternatingly coloring the edges of the 6 squares. These squares can then be distorted into rectangles, while the 8 triangles remain equilateral. The 12 diagonal square faces will become isosceles trapezoids. In the limit, the rectangles can be reduced to edges, and the trapezoids become triangles, and an icosahedron is formed, by a snub octahedron construction, , s{3,4}. (The compound of two icosahedra is constructed from both alternated positions.)

Pyritohedral symmetry variations
Uniform geometry	Nonuniform geometry	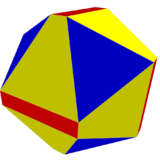Nonuniform geometry	In the limit, an icosahedron snub octahedron, , from one of two positions.	Compound of two icosahedra from both alternated positions.

Algebraic properties

Cartesian coordinates

Cartesian coordinates for the vertices of a rhombicuboctahedron centred at the origin, with edge length 2 units, are all the even permutations of

(±1, ±1, ±(1 + √2)).

If the original rhombicuboctahedron has unit edge length, its dual strombic icositetrahedron has edge lengths

[math]\displaystyle{ \frac{2}{7}\sqrt{10-\sqrt{2}} \quad \text{and} \quad \sqrt{4-2\sqrt{2}}. }[/math]

Area and volume

The area A and the volume V of the rhombicuboctahedron of edge length a are:

[math]\displaystyle{ \begin{align} A &= \left(18+2\sqrt{3}\right)a^2 &&\approx 21.464\,1016a^2 \\ V &= \frac{12+10\sqrt{2}}{3} a^3 &&\approx 8.714\,045\,21a^3. \end{align} }[/math]

Close-packing density

The optimal packing fraction of rhombicuboctahedra is given by

[math]\displaystyle{ \eta = \tfrac{4}{3} \left( 4\sqrt{2} - 5 \right) }[/math].

It was noticed that this optimal value is obtained in a Bravais lattice by de Graaf (2011). Since the rhombicuboctahedron is contained in a rhombic dodecahedron whose inscribed sphere is identical to its own inscribed sphere, the value of the optimal packing fraction is a corollary of the Kepler conjecture: it can be achieved by putting a rhombicuboctahedron in each cell of the rhombic dodecahedral honeycomb, and it cannot be surpassed, since otherwise the optimal packing density of spheres could be surpassed by putting a sphere in each rhombicuboctahedron of the hypothetical packing which surpasses it.

In the arts

Portrait of Luca Pacioli (c. 1495)

Leonardo da Vinci's illustration in Divina proportione (1509)

The 1495 Portrait of Luca Pacioli, traditionally attributed to Jacopo de' Barbari, includes a glass rhombicuboctahedron half-filled with water, which may have been painted by Leonardo da Vinci. The first printed version of the rhombicuboctahedron was by Leonardo and appeared in Pacioli's Divina proportione (1509).

A spherical 180° × 360° panorama can be projected onto any polyhedron; but the rhombicuboctahedron provides a good enough approximation of a sphere while being easy to build. This type of projection, called Philosphere, is possible from some panorama assembly software. It consists of two images that are printed separately and cut with scissors while leaving some flaps for assembly with glue.

Objects

During the Rubik's Cube craze of the 1980s, at least two twisty puzzles sold had the form of a rhombicuboctahedron (the mechanism was similar to that of a Rubik's Cube).

• 

  Sundial (1596)

• 

  Sundial

• 

  Street lamp in Mainz

• 

  Die with 18 labelled faces

• 

  Cabela's shooting target

• 

  Rubik's Snake

• 

  Rubik's Cube variation

• 

  Pyrite crystal

Related polyhedra

The rhombicuboctahedron is one of a family of uniform polyhedra related to the cube and regular octahedron.

Symmetry mutations

This polyhedron is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.

Vertex arrangement

It shares its vertex arrangement with three nonconvex uniform polyhedra: the stellated truncated hexahedron, the small rhombihexahedron (having the triangular faces and six square faces in common), and the small cubicuboctahedron (having twelve square faces in common).

Rhombicuboctahedron

Small cubicuboctahedron

Small rhombihexahedron

Stellated truncated hexahedron

Rhombicuboctahedral graph
4-fold symmetry
Vertices	24
Edges	48
Automorphisms	48
Properties	Quartic graph, Hamiltonian, regular
Table of graphs and parameters

Rhombicuboctahedral graph

The rhombicuboctahedral graph is the graph of vertices and edges of the rhombicuboctahedron. It has 24 vertices and 48 edges, and is a quartic Archimedean graph.

See also

• Compound of five rhombicuboctahedra
• Cube
• Cuboctahedron
• Nonconvex great rhombicuboctahedron
• Truncated rhombicuboctahedron
• Elongated square gyrobicupola
• Moravian star
• Octahedron
• Rhombicosidodecahedron
• Rubik's Snake – puzzle that can form a Rhombicuboctahedron "ball"
• National Library of Belarus – its architectural main component has the shape of a rhombicuboctahedron.
• Truncated cuboctahedron (great rhombicuboctahedron)

Further reading

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Section 3–9)
• Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2. 
• Coxeter, H.S.M.; Longuet-Higgins, M.S.; Miller, J.C.P. (May 13, 1954). "Uniform Polyhedra". Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences 246 (916): 401–450. doi:10.1098/rsta.1954.0003. Bibcode: 1954RSPTA.246..401C. 
• de Graaf, J.; van Roij, R.; Dijkstra, M. (2011), "Dense Regular Packings of Irregular Nonconvex Particles", Physical Review Letters 107 (15): 155501, doi:10.1103/PhysRevLett.107.155501, PMID 22107298, Bibcode: 2011PhRvL.107o5501D 
• Betke, U.; Henk, M. (2000), "Densest Lattice Packings of 3-Polytopes", Computational Geometry 16 (3): 157–186, doi:10.1016/S0925-7721(00)00007-9 
• Torquato, S.; Jiao, Y. (2009), "Dense packings of the Platonic and Archimedean solids", Nature 460 (7257): 876–879, doi:10.1038/nature08239, PMID 19675649, Bibcode: 2009Natur.460..876T 
• Hales, Thomas C. (2005), "A proof of the Kepler conjecture", Annals of Mathematics 162 (3): 1065–1185, doi:10.4007/annals.2005.162.1065 

External links

• Eric W. Weisstein, Rhombicuboctahedron (Archimedean solid) at MathWorld.
  • Weisstein, Eric W.. "Small rhombicuboctahedral graph". http://mathworld.wolfram.com/SmallRhombicuboctahedralGraph.html. 
• Klitzing, Richard. "3D convex uniform polyhedra x3o4x - sirco". https://bendwavy.org/klitzing/dimensions/polyhedra.htm. 
• The Uniform Polyhedra
• Virtual Reality Polyhedra The Encyclopedia of Polyhedra
• Editable printable net of a rhombicuboctahedron with interactive 3D view
• Rhombicuboctahedron Star by Sándor Kabai, Wolfram Demonstrations Project.
• Rhombicuboctahedron: paper strips for plaiting