Earth:Bearing (angle)

From HandWiki
Short description: In navigation, horizontal angle between the direction of an object and another object
A standard Brunton compass, used commonly by geologists and surveyors to obtain a bearing in the field

In navigation, bearing or azimuth is the horizontal angle between the direction of an object and north or another object. The angle value can be specified in various angular units, such as degrees, mils, or grad. More specifically:

  • Absolute bearing refers to the clockwise angle between the magnetic north (magnetic bearing) or true north (true bearing) and an object. For example, an object to due east would have an absolute bearing of 90 degrees. Thus, it is the same as azimuth.[1]
  • Relative bearing refers to the angle between the craft's forward direction (heading) and the location of another object. For example, an object relative bearing of 0 degrees would be immediately in front; an object relative bearing 180 degrees would be behind.[2] Bearings can be measured in mils, points, or degrees. Thus, it is the same as an azimuth difference (modulo +/- 360 degrees).

Alternatively, the US Army defines the bearing from point A to point B as the smallest angle between the ray AB and either north or south, whichever is closest. The bearing is expressed in terms of 2 characters and 1 number: first, the character is either N or S; next is the angle numerical value; third, the character representing the perpendicular direction, either E or W. The bearing angle value will always be less than 90 degrees.[1] For example, if Point B is located exactly southeast of Point A, the bearing from Point A to Point B is "S 45° E".[3] For example, if the bearing between Point A and Point B is S 45° E, the azimuth between Point A and Point B is 135°.[1][3]

Azimuths and bearings.

Types

Absolute

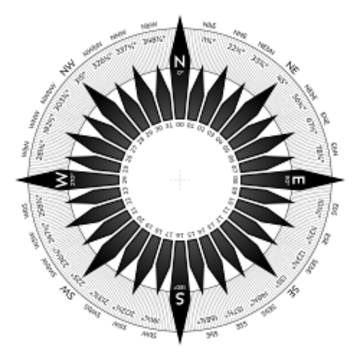
A compass rose, showing absolute bearings in degrees.

In nautical navigation the absolute bearing is the clockwise angle between north and an object observed from the vessel.

If the north used as reference is the true geographical north then the bearing is a true bearing whereas if the reference used is magnetic north then the bearing is a magnetic bearing. An absolute bearing is measured with a bearing compass.

The measurement of absolute bearings of fixed landmarks and other navigation aids is useful for the navigator because this information can be used on the nautical chart together with simple geometrical techniques to aid in determining the position of the vessel.

A grid bearing (also known as grid azimuth) is measured in relation to the fixed horizontal reference plane of grid north, that is, using the direction northwards along the grid lines of the map projection as a reference point.

A compass bearing, as in vehicle or marine navigation, is measured in relation to the magnetic compass of the navigator's vehicle or vessel (if aboard ship). It should be very close to the magnetic bearing. The difference between a magnetic bearing and a compass bearing is the deviation caused to the compass by ferrous metals and local magnetic fields generated by any variety of vehicle or shipboard sources (steel vehicle bodies/frames or vessel hulls, ignition systems, etc.)[4]

Relative

In nautical navigation the relative bearing of an object is the clockwise angle from the heading of the vessel to a straight line drawn from the observation station on the vessel to the object.

The relative bearing is measured with a pelorus or other optical and electronic aids to navigation such as a periscope, sonar system, and radar systems. Since World War II, relative bearings of such diverse point sources have been and are calibrated carefully to one another. The United States Navy operates a special range off Puerto Rico and another on the west coast to perform such systems integration. Relative bearings then serve as the baseline data for converting relative directional data into true bearings (N-S-E-W, relative to the Earth's true geography). By contrast, Compass bearings have a varying error factor at differing locations about the globe, and are less reliable than the compensated or true bearings.

The measurement of relative bearings of fixed landmarks and other navigational aids is useful for the navigator because this information can be used on the nautical chart together with simple geometrical techniques to aid in determining the vessel's position, speed, course, etc.

The measurement of relative bearings of other vessels and objects in movement is useful to the navigator in avoiding the danger of collision. For example:

  • The navigator on a ship observes a lighthouse when its relative bearing is 45° and again when it is 90°. He now knows that the distance from the ship to the lighthouse is equal to the distance travelled by the vessel between both observations.
  • The pilot of a boat observes that the relative bearing of another boat is less than 180° and decreasing (that is, it is now closer to dead ahead than before). He now knows he will pass astern of the other boat. If the bearing were to remain constant, the two boats would be on a collision course.

Examples

Piloting
A bearing can be taken on another vessel to aid piloting. If the two vessels are travelling towards each other and the relative bearing remains the same over time, there is likelihood of collision and action needs to be taken by one or both vessels to prevent this from happening.
Warfare

A bearing can be taken to a fixed or moving object in order to target it with gunfire or missiles. This is mainly used by ground troops when planning on using an air-strike on the target.

Search and rescue
A bearing can be taken to a person or vessel in distress in order to go to their aid.

Usages

The bearing between Cape Town and Melbourne along the geodesic (the shortest route) changes from 141° to 42°. Azimuthal orthographic projection and Miller cylindrical projection.

There are several methods used to measure navigation bearings including:

  1. In land navigation, a 'bearing' is ordinarily calculated in a clockwise direction starting from a reference direction of 0° and increasing to 359.9 degrees.[5] Measured in this way, a bearing is referred to as an azimuth by the US Army but not by armies in other English speaking nations, which use the term bearing.[6] If the reference direction is north (either true north, magnetic north, or grid north), the bearing is termed an absolute bearing. In a contemporary land navigation context, true, magnetic, and grid bearings are always measured in this way, with true north, magnetic north, or grid north being 0° in a 360-degree system.[5]
  2. In aircraft navigation, an angle is normally measured from the aircraft's track or heading, in a clockwise direction. If the aircraft encounters a target that is not ahead of the aircraft and not on an identical track, then the angular bearing to that target is called a relative bearing.[clarification needed][7]
  3. In marine navigation, starboard bearings are 'green' and port bearings are 'red'. Thus, in ship navigation, a target directly off the starboard side would be 'Green090' or 'G090'.[8] This method is only used for a relative bearing. A navigator on watch does not always have a corrected compass available with which to give an accurate bearing. If available, the bearing might not be numerate. Therefore, every forty-five degrees of direction from north on the compass was divided into four 'points'. Thus, 32 points of 11.25° each makes a circle of 360°. An object at 022.5° relative would be 'two points off the starboard bow', an object at 101.25° relative would be 'one point abaft the starboard beam' and an object at 213.75° relative would be 'three points on the port quarter'. This method is only used for a relative bearing.
  4. An informal method of measuring a relative bearing is by using the 'clock method'. In this method, the direction a vessel, aircraft or object is measured as if a clock face is laid over the vessel or aircraft, with the number twelve pointing forward. Something straight ahead is at 'twelve o'clock', while something directly off to the right is at 'three o'clock'. This method is only used for a relative bearing.[9]
  5. In land surveying, a bearing is the clockwise or counterclockwise angle between north or south and a direction. For example, bearings are recorded as N57°E, S51°E, S21°W, N87°W, or N15°W. In surveying, bearings can be referenced to true north, magnetic north, grid north (the Y axis of a map projection), or a previous map, which is often a historical magnetic north.[citation needed]
  6. If navigating by gyrocompass, the reference direction is true north, in which case the terms true bearing and geodetic bearing are used.
  7. In stellar navigation, the reference direction is that of the North Star, Polaris.
  8. In satellite broadcasting, a bearing is the combination of antenna azimuth and elevation required to point (aim) a satellite dish antenna in a given direction. The bearing for geostationary satellites is constant. The bearing for polar-orbiting satellites varies continuously.
A and B are near the North Pole and facing each other. Though A is facing east, B is not facing west. If B were to face west, her direction (dashed arrow) would be tangential to her latitude circle (dashed circle). Only on the equator is it true that if A faces east and B faces west that they can face each other.

Arcs

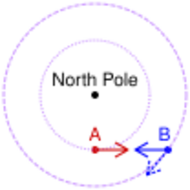
Moving from A to B along a great circle can be considered as always going in the same direction (the direction of B), but not in the sense of keeping the same bearing, which applies when following a rhumb line. Accordingly, the direction at A of B, expressed as a bearing, is not in general the opposite of the direction at B of A (when traveling on the great circle formed by A and B). For example, assume A and B in the northern hemisphere have the same latitude, and at A the direction to B is east-northeast. Then going from A to B, one arrives at B with the direction east-southeast, and conversely, the direction at B of A is west-northwest.

Latitude circles near the North Pole are shown in red. For A and B to face each other, A has to look East but B not to the West. If B were to look West, she would see a bear eyeing her as his next meal. For A and C to face each other, both would have to face North.

To "keep to a bearing" is not, in general, the same as going in a straight direction along a great circle. Conversely, one can keep to a great circle and the bearing may change. Thus the bearing of a straight path crossing the North Pole changes abruptly at the Pole from North to South. When travelling East or West, it is only on the Equator that one can keep East or West and be going straight (without the need to adjust). Anywhere else, maintaining latitude requires a change in direction, requires adjustment. This change in direction becomes increasingly negligible as one moves to a lower latitude

See also

References

  1. ↑ 1.0 1.1 1.2 U.S. Army, Advanced Map and Aerial Photograph Reading, Headquarters, War Department, Washington, D.C. (17 September 1941), pp. 24-25 [1]
  2. ↑ Rutstrum, Carl (2000). The Wilderness Route Finder. University of Minnesota Press. p. 194. ISBN 0-8166-3661-3. 
  3. ↑ 3.0 3.1 U.S. Army, Map Reading and Land Navigation, FM 21-26, Headquarters, Dept. of the Army, Washington, D.C. (28 March 1956), ch. 3, pp. 69-70
  4. ↑ Estopinal, Stephen V. (2009) (in en). A Guide to Understanding Land Surveys. John Wiley & Sons. pp. 35. ISBN 978-0-470-23058-9. https://books.google.com/books?id=g_Jvc0zBVwgC&dq=Grid+north&pg=PA35. 
  5. ↑ 5.0 5.1 Keay, pp. 133-134
  6. ↑ U.S. Army, Map Reading and Land Navigation, FM 21-26, Headquarters, Dept. of the Army, Washington, D.C. (7 May 1993), ch. 6, p. 2
  7. ↑ "Relative Bearing - an overview | ScienceDirect Topics". https://www.sciencedirect.com/topics/engineering/relative-bearing. 
  8. ↑ This method is used by the Royal Navy and the Royal Australian Navy in accordance with the Admiralty Manual of Navigation, BR45.
  9. ↑ Gilzean, Don. "Bearings" (in en-US). https://tdgil.com/bearings/. 

Further reading

  • Keay, Waly, Land Navigation: Routefinding with Map & Compass, Coventry, UK: Clifford Press Ltd. (1995), ISBN:0-319-00845-2, ISBN:978-0-319-00845-4
  • Rutstrum, Carl, The Wilderness Route Finder, University of Minnesota Press (2000), ISBN:0-8166-3661-3

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Earth:Bearing_(angle)&oldid=3298442"