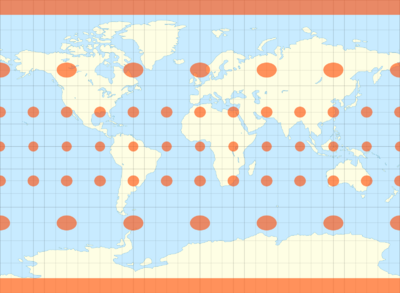
Miller cylindrical projection

The Miller cylindrical projection is a modified Mercator projection, proposed by Osborn Maitland Miller in 1942. The latitude is scaled by a factor of 4⁄5, projected according to Mercator, and then the result is multiplied by 5⁄4 to retain scale along the equator.[1] Hence:
[math]\displaystyle{ \begin{align} x &= \lambda \\ y &= \frac{5}{4}\ln\left[\tan\left(\frac{\pi}{4} + \frac{2\varphi}{5}\right)\right] = \frac{5}{4}\sinh^{-1}\left(\tan\frac{4\varphi}{5}\right)\end{align} }[/math]
or inversely,
[math]\displaystyle{ \begin{align} \lambda &= x \\ \varphi &= \frac{5}{2}\tan^{-1}e^\frac{4 y}{5} - \frac{5\pi}{8} = \frac{5}{4}\tan^{-1}\left(\sinh\frac{4 y}{5}\right)\end{align} }[/math]
where λ is the longitude from the central meridian of the projection, and φ is the latitude.[2] Meridians are thus about 0.733 the length of the equator.
In GIS applications, this projection is known as: "ESRI:54003 – World Miller Cylindrical".[3]
Compact Miller projection is similar to Miller but spacing between parallels stops growing after 55 degrees.[4]
See also
References
- ↑ Flattening the Earth: Two Thousand Years of Map Projections, John P. Snyder, 1993, pp. 179, 183, ISBN:0-226-76747-7.
- ↑ "Miller Cylindrical Projection". Wolfram MathWorld. http://mathworld.wolfram.com/MillerCylindricalProjection.html.
- ↑ "Projected coordinate systems". ESRI. http://resources.arcgis.com/en/help/arcgis-rest-api/index.html#/Projected_coordinate_systems/02r3000000vt000000/.
- ↑ Patterson, Tom; Šavrič, Bojan; Jenny, Bernhard (2015). "Introducing the Patterson Cylindrical Projection". Cartographic Perspectives (78): 77–81. doi:10.14714/CP78.1270. http://cartographicperspectives.org/index.php/journal/article/view/cp78-patterson-et-al/1362.
External links
 |