Earth:Topographic Rossby waves
Topographic Rossby waves are geophysical waves that form due to bottom irregularities. For ocean dynamics, the bottom irregularities are on the ocean floor such as the mid-ocean ridge. For atmospheric dynamics, the other primary branch of geophysical fluid dynamics, the bottom irregularities are found on land, for example in the form of mountains. Topographic Rossby waves are one of two types of geophysical waves named after the meteorologist Carl-Gustaf Rossby. The other type of Rossby waves are called planetary Rossby waves and have a different physical origin. Planetary Rossby waves form due to the changing Coriolis parameter over the earth. Rossby waves are quasi-geostrophic, dispersive waves. This means that not only the Coriolis force and the pressure-gradient force influence the flow, as in geostrophic flow, but also inertia.
Physical derivation
This section describes the mathematically simplest situation where topographic Rossby waves form: a uniform bottom slope.
Shallow water equations
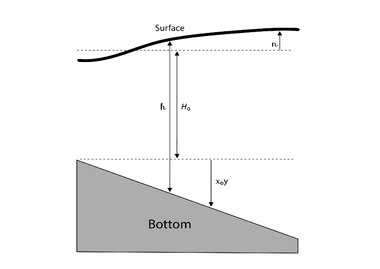
A coordinate system is defined with x in eastward direction, y in northward direction and z as the distance from the earth's surface. The coordinates are measured from a certain reference coordinate on the earth's surface with a reference latitude [math]\displaystyle{ \varphi_0 }[/math] and a mean reference layer thickness [math]\displaystyle{ H_0 }[/math]. The derivation begins with the shallow water equations:
[math]\displaystyle{ \begin{align} {\partial u\over\partial t}&+u{\partial u\over\partial x}+v{\partial u\over\partial y}-f_0v = -g{\partial \eta\over\partial x}\\[3pt] {\partial v\over\partial t}&+u{\partial v\over\partial x}+v{\partial v\over\partial y}+f_0u = -g{\partial \eta\over\partial y}\\[3pt] {\partial \eta\over\partial t}&+{\partial \over\partial x}hu + {\partial \over\partial y}hv=0, \end{align} }[/math]
where
| [math]\displaystyle{ u }[/math] | is the velocity in the x direction, or zonal velocity |
| [math]\displaystyle{ v }[/math] | is the velocity in the y direction, or meridional velocity |
| [math]\displaystyle{ h }[/math] | is the local and instantaneous fluid layer thickness |
| [math]\displaystyle{ \eta }[/math] | is the height deviation of the fluid from its mean height |
| [math]\displaystyle{ g }[/math] | is the acceleration due to gravity |
| [math]\displaystyle{ f_0 }[/math] | is the Coriolis parameter at the reference coordinate with [math]\displaystyle{ f_0 = 2 \Omega \sin(\varphi_0) }[/math], where [math]\displaystyle{ \Omega }[/math] is the angular frequency of the Earth and [math]\displaystyle{ \varphi_0 }[/math] is the reference latitude |
In the equation above, friction (viscous drag and kinematic viscosity) is neglected. Furthermore, a constant Coriolis parameter is assumed ("f-plane approximation"). The first and the second equation of the shallow water equations are respectively called the zonal and meridional momentum equations, and the third equation is the continuity equation. The shallow water equations assume a homogeneous and barotropic fluid.
Linearization
For simplicity, the system is limited by means of a weak and uniform bottom slope that is aligned with the y-axis, which in turn enables a better comparison to the results with planetary Rossby waves. The mean layer thickness [math]\displaystyle{ H }[/math] for an undisturbed fluid is then defined as
[math]\displaystyle{ H = H_0 + \alpha_0y \qquad \text{with} \qquad \alpha ={\left\vert \alpha_{0} \right\vert L \over H_0}\ll1, }[/math]
where [math]\displaystyle{ \alpha_0 }[/math] is the slope of bottom, [math]\displaystyle{ \alpha }[/math] the topographic parameter and [math]\displaystyle{ L }[/math] the horizontal length scale of the motion. The restriction on the topographic parameter guarantees that there is a weak bottom irregularity. The local and instantaneous fluid thickness [math]\displaystyle{ h }[/math] can be written as
[math]\displaystyle{ h(x,y,t)=H_0+\alpha_0 y+\eta (x,y,t). }[/math]
Utilizing this expression in the continuity equation of the shallow water equations yields
[math]\displaystyle{ {\partial \eta\over\partial t}+\left(u{\partial \eta \over\partial x}+ v{\partial \eta \over\partial y}\right)+\eta\left({\partial u \over\partial x}+{\partial v \over\partial y}\right)+ (H_0+\alpha_0y)\left({\partial u \over\partial x}+{\partial v \over\partial y}\right)+\alpha_0v=0. }[/math]
The set of equations is made linear to obtain a set of equations that is easier to solve analytically. This is done by assuming a Rossby number Ro (= advection / Coriolis force), which is much smaller than the temporal Rossby number RoT (= inertia / Coriolis force). Furthermore, the length scale of [math]\displaystyle{ \eta }[/math] [math]\displaystyle{ \Delta H }[/math] is assumed to be much smaller than the thickness of the fluid [math]\displaystyle{ H }[/math]. Finally, the condition on the topographic parameter is used and the following set of linear equations is obtained:
[math]\displaystyle{ \begin{align} {\partial u\over\partial t}&-f_0v = -g{\partial \eta\over\partial x}\\[3pt] {\partial v\over\partial t}&+f_0u = -g{\partial \eta\over\partial y}\\[3pt] {\partial \eta\over\partial t}&+H_0\left({\partial u \over\partial x} + {\partial v \over\partial y}\right)+\alpha_0v=0. \end{align} }[/math]
Quasi-geostrophic approximation
Next, the quasi-geostrophic approximation Ro, RoT [math]\displaystyle{ \ll }[/math] 1 is made, such that
[math]\displaystyle{ \begin{align} u = \bar{u}+\tilde{u} \qquad &\text{with} \qquad \bar{u}=-{g \over f_0}{\partial \eta \over \partial y}\\[3pt] v = \bar{v}+\tilde{v} \qquad &\text{with} \qquad \bar{v}={g \over f_0}{\partial \eta \over \partial x},\\[3pt] \end{align} }[/math]
where [math]\displaystyle{ \bar{u} }[/math] and [math]\displaystyle{ \bar{v} }[/math] are the geostrophic flow components and [math]\displaystyle{ \tilde{u} }[/math] and [math]\displaystyle{ \tilde{v} }[/math] are the ageostrophic flow components with [math]\displaystyle{ \tilde{u}\ll\bar{u} }[/math] and [math]\displaystyle{ \tilde{v}\ll\bar{v} }[/math]. Substituting these expressions for [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] in the previously acquired set of equations, yields:
[math]\displaystyle{ \begin{align} &-{g \over f_0}{\partial^2 \eta \over \partial y \partial t}+{\partial \tilde{u} \over\partial t}-f_0\tilde{v} = 0\\[3pt] &{g \over f_0}{\partial^2 \eta \over \partial x \partial t}+{\partial \tilde{v} \over\partial t}+f_0\tilde{u} = 0\\[3pt] &{\partial \eta\over\partial t}+H_0\left({\partial \tilde{u} \over\partial x} + {\partial \tilde{v} \over\partial y}\right)+\alpha_0 {g \over f_0}{\partial \eta \over \partial x}+ \alpha_0\tilde{v}=0. \end{align} }[/math]
Neglecting terms where small component terms ([math]\displaystyle{ \tilde{u}, \tilde{v}, {\partial\over\partial t} }[/math] and [math]\displaystyle{ \alpha_0 }[/math]) are multiplied, the expressions obtained are:
[math]\displaystyle{ \begin{align} &\tilde{v} = -{g \over f_0^2}{\partial^2 \eta \over \partial y \partial t}\\[3pt] &\tilde{u} = -{g \over f_0^2}{\partial^2 \eta \over \partial x \partial t}\\[3pt] &{\partial \eta\over\partial t}+H_0\left({\partial \tilde{u} \over\partial x} + {\partial \tilde{v} \over\partial y}\right)+\alpha_0 {g \over f_0}{\partial \eta \over \partial x}=0. \end{align} }[/math]
Substituting the components of the ageostrophic velocity in the continuity equation the following result is obtained:
[math]\displaystyle{ {\partial \eta \over\partial t}-R^2{\partial\over\partial t}\nabla^2 \eta + \alpha_0{g \over f_0}{\partial \eta \over \partial x}=0, }[/math]
in which R, the Rossby radius of deformation, is defined as
[math]\displaystyle{ R = {\sqrt{gH_0}\over f_0}. }[/math]
Dispersion relation
Taking for [math]\displaystyle{ \eta }[/math] a plane monochromatic wave of the form
[math]\displaystyle{ \eta = A \cos(k_xx+k_yy-\omega t+\phi), }[/math]
with [math]\displaystyle{ A }[/math] the amplitude, [math]\displaystyle{ k_x }[/math] and [math]\displaystyle{ k_y }[/math] the wavenumber in x- and y- direction respectively, [math]\displaystyle{ \omega }[/math] the angular frequency of the wave, and [math]\displaystyle{ \phi }[/math] a phase factor, the following dispersion relation for topographic Rossby waves is obtained:
[math]\displaystyle{ \omega = {\alpha_0 g \over f_0}{k_x \over 1+R^2(k_x^2+k_y^2)}. }[/math]
If there is no bottom slope ([math]\displaystyle{ \alpha_{0}=0 }[/math]), the expression above yields no waves, but a steady and geostrophic flow. This is the reason why these waves are called topographic Rossby waves.
The maximum frequency of the topographic Rossby waves is
[math]\displaystyle{ \left\vert \omega \right\vert _{max} ={ \left\vert \alpha_0 \right\vert g \over 2\left\vert f_0 \right\vert R }, }[/math]
which is attained for [math]\displaystyle{ k_x = R^{-1} }[/math] and [math]\displaystyle{ k_y = 0 }[/math]. If the forcing creates waves with frequencies above this threshold, no Rossby waves are generated. This situation rarely happens, unless [math]\displaystyle{ \alpha_0 }[/math] is very small. In all other cases [math]\displaystyle{ \left\vert \omega \right\vert_{max} }[/math] exceeds [math]\displaystyle{ \left\vert f_0 \right\vert }[/math] and the theory breaks down. The reason for this is that the assumed conditions: [math]\displaystyle{ \alpha \ll 1 }[/math] and RoT [math]\displaystyle{ \ll 1 }[/math] are no longer valid. The shallow water equations used as a starting point also allow for other types of waves such as Kelvin waves and inertia-gravity waves (Poincaré waves). However, these do not appear in the obtained results because of the quasi-geostrophic assumption which is used to obtain this result. In wave dynamics this is called filtering.
Phase speed
The phase speed of the waves along the isobaths (lines of equal depth, here the x-direction) is
[math]\displaystyle{ c_x = {\omega \over k_x}={\alpha_0g\over f_0}{1 \over 1 + R^2(k_x^2+k_y^2)}, }[/math]
which means that on the northern hemisphere the waves propagate with the shallow side at their right and on the southern hemisphere with the shallow side at their left. The equation of [math]\displaystyle{ c_x }[/math] shows that the phase speed varies with wavenumber so the waves are dispersive. The maximum of [math]\displaystyle{ c_x }[/math] is
[math]\displaystyle{ \left\vert c_x \right\vert_{max} = {\alpha_0g \over f_0}, }[/math]
which is the speed of very long waves ([math]\displaystyle{ k_x^2+k_y^2\rightarrow 0 }[/math]). The phase speed in the y-direction is
[math]\displaystyle{ c_y = {\omega \over k_y}={k_x \over k_y}c_x, }[/math]
which means that [math]\displaystyle{ c_y }[/math] can have any sign. The phase speed is given by
[math]\displaystyle{ c = {\omega \over k} = {k_x \over k}c_x, }[/math]
from which it can be seen that [math]\displaystyle{ \left\vert c \right\vert \leq \left\vert c_x \right\vert }[/math] as [math]\displaystyle{ \left\vert k \right\vert = \sqrt{k_x^2+k_y^2} \geq \left\vert k_x \right\vert }[/math]. This implies that the maximum of [math]\displaystyle{ \left\vert c_x \right\vert }[/math] is the maximum of [math]\displaystyle{ \left\vert c \right\vert }[/math].[1]
Analogy between topographic and planetary Rossby waves
Planetary and topographic Rossby waves are the same in the sense that, if the term [math]\displaystyle{ {\alpha_0 g/f_0} }[/math] is exchanged for [math]\displaystyle{ -\beta_0R^2 }[/math] in the expressions above, where [math]\displaystyle{ \beta_0 }[/math] is the beta-parameter or Rossby parameter, the expression of planetary Rossby waves is obtained. The reason for this similarity is that for the nonlinear shallow water equations for a frictionless, homogeneous flow the potential vorticity q is conserved:
[math]\displaystyle{ {dq \over dt}=0 \qquad \text{with} \qquad q={\zeta + f \over h}, }[/math]
with [math]\displaystyle{ \zeta }[/math] being the relative vorticity, which is twice the rotation speed of fluid elements about the z-axis, and is mathematically defined as
[math]\displaystyle{ \zeta = {\partial v \over \partial x}-{\partial u \over \partial y}, }[/math]
with [math]\displaystyle{ \zeta \gt 0 }[/math] an anticlockwise rotation about the z-axis. On a beta-plane and for a linearly sloping bottom in the meridional direction, the potential vorticity becomes
[math]\displaystyle{ q = {f_0+\beta_0 y + \zeta \over H_0 + \alpha_0 y + \eta}. }[/math].
In the derivations above it was assumed that
[math]\displaystyle{ \begin{align} \beta_0L \ll \left\vert f_0 \right\vert &\text{ : small planetary number }\beta \\[3pt] [\zeta] \ll \left\vert f_0 \right\vert &\text{ : small Rossby number Ro}\\[3pt] \alpha_0L \ll H_0&\text{ : small topographic parameter }\alpha \\[3pt] \Delta H \ll H &\text{ : linear dynamics}, \end{align} }[/math]
so
[math]\displaystyle{ q = { f_0 \left(1+{\beta_0y \over f_0} + {\zeta \over f_0} \right)\over H_0 \left(1+{\alpha_0y \over H_0}+ {\eta \over H_0}\right)}={f_0\over H_0} \left(1+{\beta_0y \over f_0} + {\zeta \over f_0} \right)\left(1-{\alpha_0y \over H_0}- {\eta \over H_0} + \ldots\right), }[/math]
where a Taylor expansion was used on the denominator and the dots indicate higher order terms. Only keeping the largest terms and neglecting the rest, the following result is obtained:
[math]\displaystyle{ q\approx {f_0 \over H_0}\left(1+{\beta_0y \over f_0} + {\zeta \over f_0}-{\alpha_0y \over H_0} -{\eta \over H_0}\right). }[/math]
Consequently, the analogy that appears in potential vorticity is that [math]\displaystyle{ \beta_0/f_0 }[/math] and [math]\displaystyle{ -\alpha_0/H_0 }[/math] play the same role in the potential vorticity equation. Rewriting these terms a bit differently, this boils down to the earlier seen [math]\displaystyle{ -\beta_0R^2 }[/math] and [math]\displaystyle{ {\alpha_0 g/f_0} }[/math], which demonstrates the similarity between planetary and topographic Rossby waves. The equation for potential vorticity shows that planetary and topographic Rossby waves exist because of a background gradient in potential vorticity.
The analogy between planetary and topographic Rossby waves is exploited in laboratory experiments that study geophysical flows to include the beta effect which is the change of the Coriolis parameter over the earth. The water vessels used in those experiments are far too small for the Coriolis parameter to vary significantly. The beta effect can be mimicked to a certain degree in these experiments by using a tank with a sloping bottom. The substitution of the beta effect by a sloping bottom is only valid for a gentle slope, slow fluid motions and in the absence of stratification.[1]
Conceptual explanation
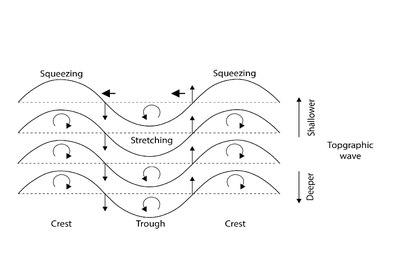
As shown in the last section, Rossby waves are formed because potential vorticity must be conserved. When the surface has a slope, the thickness of the fluid layer [math]\displaystyle{ h }[/math] is not constant. The conservation of the potential vorticity forces the relative vorticity [math]\displaystyle{ \zeta }[/math] or the Coriolis parameter [math]\displaystyle{ f }[/math] to change. Since the Coriolis parameter is constant at a given latitude, the relative vorticity must change. In the figure a fluid moves to a shallower environment, where [math]\displaystyle{ h }[/math] is smaller, causing the fluid to form a crest. When the height is smaller, the relative vorticity must also be smaller. In the figure, this becomes a negative relative vorticity (on the northern hemisphere a clockwise spin) shown with the rounded arrows. On the southern hemisphere this is an anticlockwise spin, because the Coriolis parameter is negative on the southern hemisphere. If a fluid moves to a deeper environment, the opposite is true. The fluid parcel on the original depth is sandwiched between two fluid parcels with one of them having a positive relative vorticity and the other one a negative relative vorticity. This causes a movement of the fluid parcel to the left in the figure. In general, the displacement causes a wave pattern that propagates with the shallower side to the right on the northern hemisphere and to the left on the southern hemisphere.[1]

Measurements of topographic Rossby waves on earth
From 1 January 1965 till 1 January 1968, The Buoy Project at the Woods Hole Oceanographic Institution dropped buoys on the western side of the Northern Atlantic to measure the velocities. The data has several gaps because some of the buoys went missing. Still they managed to measure topographic Rossby waves at 500 meters depth.[2] Several other research projects have confirmed that there are indeed topographic Rossby waves in the Northern Atlantic.[3][4][5]
In 1988, barotropic planetary Rossby waves were found in the Northwest Pacific basin.[6] Further research done in 2017 concluded that the Rossby waves are no planetary Rossby waves, but topographic Rossby waves.[7]
In 2021, research in the South China Sea confirmed that topographic Rossby waves exist.[8][9]
In 2016, research in the East Mediterranean showed that topographic Rossby Waves are generated south of Crete due to lateral shifts of a mesoscale circulation structure over the sloping bottom at 4000 m (https://doi.org/10.1016/j.dsr2.2019.07.008).
References
- ↑ Jump up to: 1.0 1.1 1.2 Cushman-Roisin, Benoit; Beckers, Jean-Marie (2011), Introduction, International Geophysics, 101, Elsevier, pp. 3–39, doi:10.1016/b978-0-12-088759-0.00001-8, ISBN 9780120887590, http://dx.doi.org/10.1016/b978-0-12-088759-0.00001-8, retrieved 2022-03-17
- ↑ Jump up to: 2.0 2.1 Thompson, Rory (January 1971). "Topographic Rossby waves at a site north of the Gulf Stream". Deep Sea Research and Oceanographic Abstracts 18 (1): 1–19. doi:10.1016/0011-7471(71)90011-8. ISSN 0011-7471. Bibcode: 1971DSRA...18....1T. http://dx.doi.org/10.1016/0011-7471(71)90011-8.
- ↑ Louis, John P.; Petrie, Brian D.; Smith, Peter C. (January 1982). <0047:ootrwo>2.0.co;2 "Observations of Topographic Rossby Waves on the Continental Margin off Nova Scotia". Journal of Physical Oceanography 12 (1): 47–55. doi:10.1175/1520-0485(1982)012<0047:ootrwo>2.0.co;2. ISSN 0022-3670. Bibcode: 1982JPO....12...47L. http://dx.doi.org/10.1175/1520-0485(1982)012<0047:ootrwo>2.0.co;2.
- ↑ Oey, L-Y.; Lee, H-C. (December 2002). "Deep Eddy Energy and Topographic Rossby Waves in the Gulf of Mexico". Journal of Physical Oceanography 32 (12): 3499–3527. doi:10.1175/1520-0485(2002)032<3499:deeatr>2.0.co;2. ISSN 0022-3670. Bibcode: 2002JPO....32.3499O.
- ↑ Hamilton, Peter (July 2009). "Topographic Rossby waves in the Gulf of Mexico". Progress in Oceanography 82 (1): 1–31. doi:10.1016/j.pocean.2009.04.019. ISSN 0079-6611. Bibcode: 2009PrOce..82....1H. http://dx.doi.org/10.1016/j.pocean.2009.04.019.
- ↑ Schmitz, William J. (March 1988). <0459:eotefi>2.0.co;2 "Exploration of the Eddy Field in the Midlatitude North Pacific". Journal of Physical Oceanography 18 (3): 459–468. doi:10.1175/1520-0485(1988)018<0459:eotefi>2.0.co;2. ISSN 0022-3670. Bibcode: 1988JPO....18..459S. http://dx.doi.org/10.1175/1520-0485(1988)018<0459:eotefi>2.0.co;2.
- ↑ Miyamoto, Masatoshi; Oka, Eitarou; Yanagimoto, Daigo; Fujio, Shinzou; Mizuta, Genta; Imawaki, Shiro; Kurogi, Masao; Hasumi, Hiroyasu (May 2017). "Characteristics and mechanism of deep mesoscale variability south of the Kuroshio Extension". Deep Sea Research Part I: Oceanographic Research Papers 123: 110–117. doi:10.1016/j.dsr.2017.04.003. ISSN 0967-0637. Bibcode: 2017DSRI..123..110M. http://dx.doi.org/10.1016/j.dsr.2017.04.003.
- ↑ QUAN, QI; CAI, ZHONGYA; JIN, GUANGZHEN; LIU, ZHIQIANG (2021-03-22). "Topographic Rossby Waves in the Abyssal South China Sea". Journal of Physical Oceanography 51 (6): 1795. doi:10.1175/jpo-d-20-0187.1. ISSN 0022-3670. Bibcode: 2021JPO....51.1795Q.
- ↑ Wang, Qiang; Zeng, Lili; Shu, Yeqiang; Li, Jian; Chen, Ju; He, Yunkai; Yao, Jinglong; Wang, Dongxiao et al. (October 2019). "Energetic Topographic Rossby Waves in the Northern South China Sea". Journal of Physical Oceanography 49 (10): 2697–2714. doi:10.1175/jpo-d-18-0247.1. ISSN 0022-3670. Bibcode: 2019JPO....49.2697W. http://dx.doi.org/10.1175/jpo-d-18-0247.1.
 |