Engineering:Class of accuracy in electrical measurements

Short description: Accuracy in electrical measurement

In electrical engineering class of accuracy is a figure which represents the error tolerance of a measuring device.

Class of accuracy

Measuring devices are labelled for the class of accuracy. This figure is the percentage of the inherent error of the measuring device with respect to full scale deflection. For example, if the class of accuracy is 2 that means an error of 2 volts in a full scale 100 volt reading.

Measurement

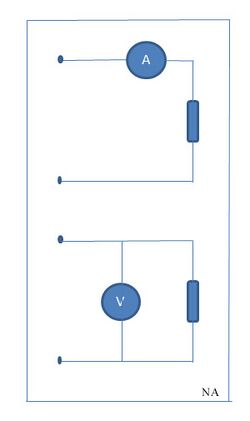
In electrical engineering, characteristics like current or voltage can be measured by an ammeter, a voltmeter, a multimeter, etc. The ammeter is used in series with the load, so the same current flows through the load and the ammeter. The voltmeter is used in parallel with the load, so the voltage between the two terminals of the load is equal to the voltage between the two terminals of the voltmeter. Ideally the measuring device should not affect the circuit parameters i.e., the internal impedance of the ammeter should be zero (no voltage drop over the ammeter) and the internal impedance of the voltmeter should be infinite (no current through the voltmeter). However, in actual case, ammeters have a low but non zero impedance and voltmeters have a high but not infinite internal impedance. Thus the measured parameters are somewhat altered during the measurements.

Example

Let V be the voltage (EMF) of the source R be the resistance of the load and r be the resistance of the ammeter. The current through the load is I

[math]\displaystyle{ I=\frac{V}{R} }[/math]

When the ammeter is connected in series with the load the current I₂ is

[math]\displaystyle{ I_2=\frac{V}{R+r} }[/math]

The difference introduced by the measuring device is then,

[math]\displaystyle{ \Delta I = I-I_2 =\frac{V\cdot r}{R^2+R\cdot r}\approx\frac{V\cdot r}{R^2} }[/math]

The ratio of the difference to the actual value is

[math]\displaystyle{ \frac{\Delta I}{I}\approx\frac{r}{R} }[/math]