Engineering:Damping factor

From HandWiki

In an audio system, the damping factor is defined as the ratio of the rated impedance of the loudspeaker (usually assumed to be 8 Ω) to the source impedance of the power amplifier,[1][2][3][4][5][6] and was proposed in 1941.[7] Only the magnitude of the loudspeaker impedance is used, and the power amplifier output impedance is assumed to be totally resistive.

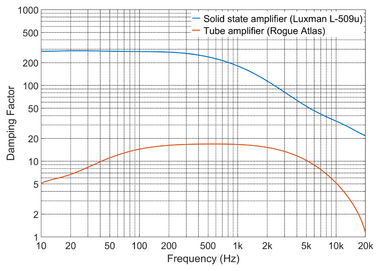
Comparison of damping factors for a solid state amplifier (Luxman L-509u) and a tube amplifier (Rogue Atlas)

In typical solid state and tube amplifiers, the damping factor varies as a function of frequency. In solid state amplifiers, the damping factor usually has a maximum value at low frequencies, and it reduces progressively at higher frequencies. The figure to the right shows the damping factor of two amplifiers. One is a solid state amplifier (Luxman L-509u) and the other is a tube amplifier (Rogue Atlas). These results are fairly typical of these two types of amplifiers, and they serve to illustrate the fact that tube amplifiers usually have much lower damping factors than modern solid state amplifiers, which is an undesirable characteristic.

Calculation

The source impedance (that is seen by the loudspeaker) includes the connecting cable impedance. The load impedance [math]\displaystyle{ Z_\mathrm{L} }[/math] and the source impedance [math]\displaystyle{ Z_\mathrm{S} }[/math] are shown in the circuit diagram.

Source and load circuit Z (2).svg

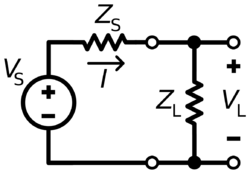
The definition of damping factor [math]\displaystyle{ DF }[/math] normally used to characterize audio amplifiers is:[7] [math]\displaystyle{ DF = \frac{Z_\mathrm{L}}{Z_\mathrm{S}} }[/math]

However, in this form [math]\displaystyle{ DF }[/math] is not in fact proportional to the electrical circuit damping. The load is the source of energy being damped, and if [math]\displaystyle{ Z_\mathrm{S} }[/math] = 0, the damping resistance in series with the energy source cannot fall below [math]\displaystyle{ Z_\mathrm{L} }[/math] itself (unless [math]\displaystyle{ Z_\mathrm{S} }[/math] is made negative, which is usually impractical). This fact was admitted and an improved definition was proposed:[8] [math]\displaystyle{ DF = \frac{Z_\mathrm{L}+Z_\mathrm{S}}{Z_\mathrm{L}} }[/math] But the former definition has nevertheless become standard.

Explanation

Pierce[4] undertook an analysis of the effects of amplifier damping factor on the decay time and frequency-dependent response variations of a closed-box, acoustic suspension loudspeaker system. The results indicated that any damping factor over 10 is going to result in inaudible differences between that and a damping factor equal to infinity. However, it was also determined that the frequency-dependent variation in the response of the loudspeaker due to the output resistance of the amplifier is much more significant than the effects on system damping. It is also important to not confuse these effects with damping effects, as they are caused by two quite different mechanisms. The calculations suggested that a damping factor in excess of 50 will not lead to audible improvements, all other things being equal.[4]

For audio power amplifiers employing some global negative feedback, this source impedance [math]\displaystyle{ Z_\mathrm{S} }[/math] is generally smaller than 0.1 Ω,[6] which from the point of view of the driver voice coil is a near short circuit.

The loudspeaker's nominal load impedance (input impedance) of [math]\displaystyle{ Z_\mathrm{L} }[/math] is usually around 4 to 8 Ω, although other impedance speakers are available, sometimes dropping as low as 1 Ω or 2 Ω. However, the impedance rating of a loudspeaker is simply a number that indicates the nominal minimum impedance of that loudspeaker over a representative portion of its operating frequency range. It needs to be kept in mind that most loudspeakers have an impedance that varies considerably with frequency.[6][9] For a dynamic loudspeaker driver, a peak in the impedance is present at the free-air resonance frequency of the driver, which can be significantly greater in magnitude than the nominal rated impedance. In addition, the electrical characteristics of every voice coil will change with temperature (high power levels increase voice coil temperature, and thus resistance), the inductance of voice-coil windings leads to a rising impedance at high frequencies, and passive crossover networks (composed of relatively large inductors, capacitors, and resistors) introduce further impedance variations in multi-way loudspeaker systems. Referring to the equation for [math]\displaystyle{ DF }[/math] that was given above, this frequency-dependent variation in loudspeaker load impedance results in the value of the damping factor of the amplifier varying with frequency when it is connected to a loudspeaker impedance load.

In loudspeaker systems, the value of the damping factor between a particular loudspeaker and a particular amplifier describes the ability of the amplifier to control undesirable movement of the speaker cone near the resonant frequency of the speaker system.[3] It is usually used in the context of low-frequency driver behavior, and especially so in the case of electrodynamic drivers, which use a magnetic motor to generate the forces which move the diaphragm. A high damping factor in an amplifier is sometimes considered to result in the amplifier having greater control over the movement of the speaker cone,[3] particularly in the bass region near the resonant frequency of the driver's mechanical resonance.

Speaker diaphragms have mass, and their compliant suspension components have stiffness. Together, these form a resonant system, and the mechanical cone resonance may be excited by electrical signals (for example, pulses) at audio frequencies. But a driver with a voice coil is also a current generator, since it has a coil attached to the cone and suspension, and that coil is immersed in a magnetic field. For every motion the coil makes, it will generate a current that will be seen by any electrically attached equipment, such as an amplifier. In fact, the output circuitry of the amplifier will be the main electrical load on the "voice coil current generator". If that load has low resistance, the current will be larger, and the voice coil will be more strongly forced to decelerate. A high damping factor (which requires low output impedance at the amplifier output) very rapidly damps unwanted cone movements induced by the mechanical resonance of the speaker, acting as the equivalent of a "brake" on the voice coil motion (just as a short circuit across the terminals of a rotary electrical generator will make it very hard to turn). It is generally (though not universally) thought that tighter control of voice coil motion is desirable, as it is believed to contribute to better-quality sound.[citation needed]

The damping circuit

The voltage generated by the moving voice coil forces current through three resistances:

  • The resistance of the voice coil itself
  • The resistance of the interconnecting cable
  • The output resistance of the amplifier

Effect of voice coil resistance

This is the key factor in limiting the amount of damping that can be achieved electrically, because its value is larger (say between 4 and 8 Ω typically) than any other resistance in the output circuitry of an amplifier that does not use an output transformer (nearly every solid-state amplifier on the mass market).

A loudspeaker's flyback current is not only dissipated through the amplifier output circuit, but also through the internal resistance of the loudspeaker itself. Therefore, the choice of different loudspeakers will lead to different damping factors when coupled with the same amplifier.

Effect of cable resistance

The damping factor is affected to some extent by the resistance of the speaker cables.[2][6] The higher the resistance of the speaker cables, the lower the damping factor.

Amplifier output impedance

Modern solid state amplifiers, which use relatively high levels of negative feedback to control distortion, have very low output impedances—one of the many consequences of using feedback—and small changes in an already low value change overall damping factor by only a small, and therefore negligible, amount.

Thus, high damping factor values do not, by themselves, say very much about the quality of a system; most modern amplifiers have them, but vary in quality nonetheless.

Vacuum-tube amplifiers typically have much lower feedback ratios, and in any case almost always have output transformers that limit how low the output impedance can be. Their lower damping factors are one of the reasons many audiophiles prefer tube amplifiers. Taken even further, some tube amplifiers are designed to have no negative feedback at all.

In practice

Typical modern solid-state amplifiers with negative feedback tend to have high damping factors, usually above 50 and sometimes even greater than 150. High damping factors tend to reduce the extent to which a loudspeaker "rings" (undergoes unwanted short-term oscillation after an impulse of power is applied), but the extent to which damping factors higher than about 20 help in this respect is easily overstated;[2] there will be significant effective internal resistance, as well as some resistance and reactance in crossover networks and speaker cables.[1] Older amplifiers, plus modern triode and even solid-state amplifiers with low negative feedback, will tend to have damping factors closer to unity, or even less than 1.[citation needed]

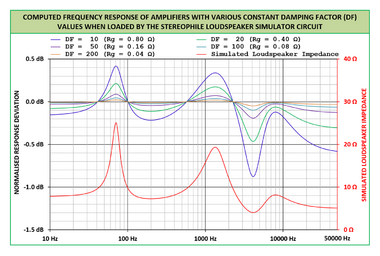
Effects of amplifier damping factor on the frequency response when connected to a simulated impedance load typical of a two-way closed box loudspeaker system

Although extremely high values of damping factor in an amplifier will not necessarily make the loudspeaker–amplifier combination sound better,[10] a high damping factor can serve to reduce the intensity of added frequency response variations that are undesirable. The figure on the right shows the effect of damping factor on the frequency response of an amplifier when that amplifier is connected to a simulated loudspeaker impedance load. This load is moderately demanding but not untypical of high-fidelity loudspeakers that are on the market, and it is based on the circuit proposed by Atkinson.[11] The audio magazines Stereophile and Australian Hi-Fi have recognised the importance of amplifier damping factor, and have made the use of the simulated loudspeaker load a routine part of their amplifier measurements. At around 4 kHz, the real-life difference between an amplifier with a moderate (100) damping factor and one with a low (20) damping factor is about 0.37 dB. However, the amplifier with the low damping factor is acting more like a subtle graphic equaliser than is the amplifier with the moderate damping factor, where the peaks and dips in the amplifier's frequency response correspond closely to the peaks and dips in the loudspeaker impedance response.[9]

It is clear from the various amplifier frequency response curves that low damping factor values result in significant changes in the frequency response of the amplifier in a number of frequency bands. This will result in broad levels of sound coloration that are highly likely to be audible. In addition, the frequency response changes will depend on the frequency-dependent impedance of whichever loudspeaker happens to be connected to the amplifier.[9] Hence, in high-fidelity sound reproduction systems, amplifiers with moderate to high damping factors are the preferred option if accurate sound reproduction is desired when those amplifiers are connected to typical multi-way loudspeaker impedance loads.

Some amplifier designers, such as Nelson Pass, claim that loudspeakers can sound better with lower electrical damping,[12] although this may be attributed to listener preference rather than technical merit. A lower damping factor helps to enhance the bass response of the loudspeaker by several decibels (where the impedance of the speaker would be at its maximum), which is useful if only a single speaker is used for the entire audio range. Therefore, some amplifiers, in particular vintage amplifiers from the 1950s, 1960s and 1970s, feature controls for varying the damping factor. While such bass "enhancement" may be pleasing to some listeners, it nonetheless represents a distortion of the input signal.[citation needed]

One example of a vintage amplifier with a damping control is the Accuphase E-202, which has a three-position switch described by the following excerpt from its owner's manual:[13]

Speaker Damping Control enhances characteristic tonal qualities of speakers. The damping factor of solid state amplifiers is generally very large and ideal for damping the speakers. However, some speakers require an amplifier with a low damping factor to reproduce rich, full-bodied sound. The E-202 has a Speaker Damping Control which permits choice of three damping factors and induces maximum potential performance from any speaker. Damping factor with an 8 Ω load becomes more than 50 when this control is set to NORMAL. Likewise, it is 5 at MEDIUM position, and 1 at SOFT position. It enables choosing the speaker sound that one prefers.

Damping is also a concern in guitar amplifiers (an application in which controlled distortion is desirable) and low damping can be better. Numerous guitar amplifiers have damping controls, and the trend to include this feature has been increasing since the 1990s. For instance the Marshall Valvestate 8008 rack-mounted stereo amplifier has a switch between "linear" and "Valvestate" mode:[14]

"Linear/Vstate selector. Slide to select linear or Valvestate performance. The Valvestate mode gives extra warm harmonics plus the richness of tone, which is unique to the Valvestate power stage. Linear mode produces a highly defined hi-fi tone that gives a totally different character to the sound and suits certain modern "metal" styles, or PA applications."

This is actually a damping control based on negative current feedback, which is evident from the schematic,[15] where the same switch is labeled as "Output Power Mode: Current/Voltage".

See also


References

  1. ↑ 1.0 1.1 Augspurger, George L. (January 1967). Stocklin, William A.. ed. "The Damping Factor Debate". Electronics World (Chicago, Illinois: Ziff Davis) 77 (1): 46–47. https://archive.org/details/Electronics_World_1967_01. 
  2. ↑ 2.0 2.1 2.2 Toole, Floyd E. (February 1975). Welling, Ernie. ed. "Damping, Damping Factor, and Damn Nonsense". AudioScene Canada (Toronto, Ontario: Maclean-Hunter) 12 (2): 16–17. https://archive.org/details/sim_audio-video-canada_1975-02_12_2. 
  3. ↑ 3.0 3.1 3.2 Ballou, Glen, ed (1987). Handbook for Sound Engineers: The New Audio Cyclopedia. IN, USA: Howard W. Sams & Company. 
  4. ↑ 4.0 4.1 4.2 Pierce, Dick (2002). "Damping Factor: Effects On System Response". http://www.cartchunk.org/audiotopics/DampingFactor.pdf. 
  5. ↑ Sinclair, Ian, ed (2009). Audio Engineering: Know It All. United Kingdom: Newnes. 
  6. ↑ 6.0 6.1 6.2 6.3 Duncan, Ben (1997). High Performance Audio Power Amplifiers for Music Performance and Reproduction. United Kingdom: Newnes. ISBN 0-7506-2629-1. 
  7. ↑ 7.0 7.1 Langford-Smith, F. (1941), Radiotron Designer’s Handbook, 3rd ed., The Wireless Press, p15
  8. ↑ Langford-Smith, F. (1955), Damping Factor: A New Approach. Wireless World, August, p367.
  9. ↑ 9.0 9.1 9.2 Norton, Thomas J. (6 January 1994). "Questions of Impedance Interaction". AVTech Media. https://www.stereophile.com/reference/810/index.html. 
  10. ↑ Elliott, Rod (20 January 2010). "Impedance, and how it affects audio equipment". https://sound-au.com/impedance.htm. 
  11. ↑ Atkinson, John (19 August 1995). "Real-Life Measurements". AVTech Media. https://www.stereophile.com/reference/60/index.html. 
  12. ↑ Pass, Nelson (2004). "Current Source Amplifiers and Sensitive / Full-Range Drivers". http://www.firstwatt.com/pdf/art_cs_amps.pdf. 
  13. ↑ "Accuphase E-202 Integrated Stereo Amplifier". https://www.fmtunerinfo.com/T-101brochure.pdf. 
  14. ↑ "Marshall Valvestate Power Amplifiers Handbook". https://drtube.com/schematics/marshall/8004-8008-hbk.pdf. 
  15. ↑ "Marshall 8008 Valvestate Schematic". http://www.drtube.com/schematics/marshall/8008.pdf. 

Further reading

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Engineering:Damping_factor&oldid=3255610"