Engineering:Necking (engineering)

Short description: Highly localized tensile deformation

The above image shows a test specimen, when of a certain kind of material, and experienced under a great enough load, experiences necking. The portion where necking occurs may be called the neck of the specimen.

In engineering and materials science, necking is a mode of tensile deformation where relatively large amounts of strain localize disproportionately in a small region of the material. The resulting prominent decrease in local cross-sectional area provides the basis for the name "neck". Because the local strains in the neck are large, necking is often closely associated with yielding, a form of plastic deformation associated with ductile materials, often metals or polymers. Once necking has begun, the neck becomes the exclusive location of yielding in the material, as the reduced area gives the neck the largest local stress.

Formation

Necking results from an instability during tensile deformation when the cross-sectional area of the sample decreases by a greater proportion than the material strain hardens. Armand Considère published the basic criterion for necking in 1885, in the context of the stability of large scale structures such as bridges. Three concepts provide the framework for understanding neck formation.

1. Before deformation, all real materials have heterogeneities such as flaws or local variations in dimensions or composition that cause local fluctuations in stresses and strains. To determine the location of the incipient neck, these fluctuations need only be infinitesimal in magnitude.
2. During plastic tensile deformation the material decreases in cross-sectional area due to the incompressibility of plastic flow. (Not due to the Poisson effect, which is linked to elastic behaviour.)
3. During plastic tensile deformation the material strain hardens. The amount of hardening varies with extent of deformation.

The latter two effects determine the stability while the first effect determines the neck's location.

The Considère treatment

Instability (onset of necking) is expected to occur when an increase in the (local) strain produces no net increase in the load, F. This will happen when

[math]\displaystyle{ \Delta F = 0 }[/math]

This leads to

[math]\displaystyle{ \begin{align} & F = A \sigma_T \\[4pt] \implies & dF = A d \sigma_T + \sigma_T dA = 0 \\[4pt] \implies & \frac{d\sigma_T}{\sigma_T} = -\frac{dA}{A} = \frac{dL}{L} = d\varepsilon_T \\ \implies & \sigma_T = \frac{d\sigma_T}{d\varepsilon_T} \end{align} }[/math]

with the T subscript being used to emphasize that these stresses and strains must be true values. Necking is thus predicted to start when the slope of the true stress / true strain curve falls to a value equal to the true stress at that point.

Application to metals

Necking commonly arises in both metals and polymers. However, while the phenomenon is caused by the same basic effect in both materials, they tend to have different types of (true) stress-strain curve, such that they should be considered separately in terms of necking behaviour. For metals, the (true) stress tends to rise monotonically with increasing strain, although the gradient (work hardening rate) tends to fall off progressively. This is primarily due to a progressive fall in dislocation mobility, caused by interactions between them. With polymers, on the other hand, the curve can be more complex. For example, the gradient can in some cases rise sharply with increasing strain, due to the polymer chains becoming aligned as they reorganise during plastic deformation. This can lead to a stable neck. No effect of this type is possible in metals.

The figure shows a screenshot from an interactive simulation available on the DoITPoMS educational website. The construction is shown for a (true) stress-strain curve represented by a simple analytical expression (Ludwik-Hollomon).

The Considère construction for prediction of the onset of necking, expressed as the gradient of the (true) stress-strain curve falling to the true stress, for a material conforming to the Ludwik-Hollomon relationship, with the parameter values shown.

The condition can also be expressed in terms of the nominal strain:

[math]\displaystyle{ \begin{align} \frac{d\sigma_T}{d\varepsilon_T} &= \frac{d\sigma_T}{d\varepsilon_N} \frac{d\varepsilon_N}{d\varepsilon_T} \\[4pt] &= \frac{d\sigma_T}{d\varepsilon_N} \frac{dL/L_0}{dL/L} \\[4pt] &= \frac{d\sigma_T}{d\varepsilon_N} \frac{L}{L_0} \\[4pt] &= \frac{d\sigma_T}{d\varepsilon_N} (1 + \varepsilon_\mathrm{N}) \end{align} }[/math]

Therefore, at the instability point:

[math]\displaystyle{ \sigma_T = \frac{d\sigma_T}{d\varepsilon_N} (1 + \varepsilon_N) }[/math]

It can therefore also be formulated in terms of a plot of true stress against nominal strain. On such a plot, necking will start where a line from the point ε_N = –1 forms a tangent to the curve. This is shown in the next figure, which was obtained using the same Ludwik-Hollomon representation of the true stress – true strain relationship as that of the previous figure.

The Considère construction for prediction of the onset of necking, expressed as the point where the gradient of the true stress – nominal strain curve extrapolates back to a nominal strain of -1 at zero stress, for a material conforming to the Ludwik-Hollomon relationship, with the parameter values shown.

Importantly, the condition also corresponds to a peak (plateau) in the nominal stress – nominal strain plot. This can be seen on obtaining the gradient of such a plot by differentiating the expression for σ_N with respect to ε_N.

[math]\displaystyle{ \begin{align} \sigma_N &= \frac{\sigma_T}{1 + \varepsilon_N} \\[4pt] \therefore \frac{d\sigma_N}{d\varepsilon_N} &= \frac{d\sigma_T}{d\varepsilon_N} \frac{1}{1 + \varepsilon_N}- \frac{\sigma_T}{(1 + \varepsilon_N)^2} \end{align} }[/math]

Substituting for the true stress – nominal strain gradient (at the onset of necking):

[math]\displaystyle{ \frac{d\sigma_N}{d\varepsilon_N} = \frac{\sigma_T}{1 + \varepsilon_N} \frac{1}{1 + \varepsilon_N} - \frac{\sigma_T}{(1 + \varepsilon_N)^2} = 0 }[/math]

This condition can also be seen in the two figures. Since many stress-strain curves are presented as nominal plots, and this is a simple condition that can be identified by visual inspection, it is in many ways the easiest criterion to use to establish the onset of necking. It also corresponds to the “strength” (ultimate tensile stress), at least for metals that do neck (which covers the majority of “engineering” metals). On the other hand, the peak in a nominal stress-strain curve is commonly a fairly flat plateau, rather than a sharp maximum, so accurate assessment of the strain at the onset of necking may be difficult. Nevertheless, this strain is a meaningful indication of the “ductility” of the metal – more so than the commonly-used “nominal strain at fracture”, which depends on the aspect ratio of the gauge length of the tensile test-piece – see the article on ductility.

Application to polymers

The tangent construction shown above is rarely used in interpreting the stress-strain curves of metals. However, it is popular for analysis of the tensile drawing of polymers. (since it allows study of the regime of stable necking). It may be noted that, for polymers, the strain is commonly expressed as a “draw ratio”, rather than a strain: in this case, extrapolation of the tangent is carried out to a draw ratio of zero, rather than a strain of -1.

Graphical construction indicating criteria for neck formation and neck stabilization.

Graphical construction for a material that deforms homogeneously at all draw ratios.

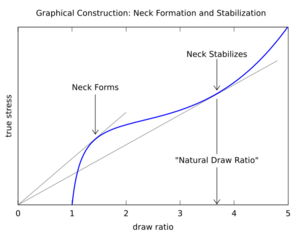
The plots relate (top) to a material that forms a stable neck and (bottom) a material that deforms homogeneously at all draw ratios.

As deformation proceeds, the geometric instability causes strain to continue concentrating in the neck until the material either ruptures or the necked material hardens enough, as indicated by the second tangent point in the top diagram, to cause other regions of the material to deform instead. The amount of strain in the stable neck is called the natural draw ratio because it is determined by the material's hardening characteristics, not the amount of drawing imposed on the material. Ductile polymers often exhibit stable necks because molecular orientation provides a mechanism for hardening that predominates at large strains.

See also

• Stress–strain curve
• Trace necking
• Universal testing machine