Engineering:Pareto front

Short description: Set of all Pareto efficient situations

In multi-objective optimization, the Pareto front (also called Pareto frontier or Pareto curve) is the set of all Pareto efficient solutions. Colloquially, this means when there are many distinct objectives to consider in an optimization problem, a Pareto front represents the set of solutions where no solution outperforms any other solution in the set at every objective, and every solution not in the set is outperformed by at least one solution in the Pareto front in every objective. The concept is widely used in engineering. It allows the designer to restrict attention to the set of efficient choices, and to make tradeoffs within this set, rather than considering the full range of every parameter.

Example of a Pareto frontier. The boxed points represent feasible choices, and smaller values are preferred to larger ones. Point C is not on the Pareto frontier because it is dominated by both point A and point B. Points A and B are not strictly dominated by any other, and hence lie on the frontier.

A production-possibility frontier. The red line is an example of a Pareto-efficient frontier, where the frontier and the area left and below it are a continuous set of choices. The red points on the frontier are examples of Pareto-optimal choices of production. Points off the frontier, such as N and K, are not Pareto-efficient, since there exist points on the frontier which Pareto-dominate them.

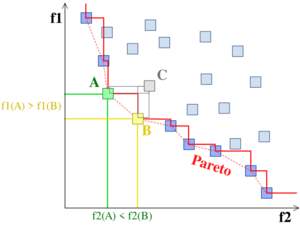
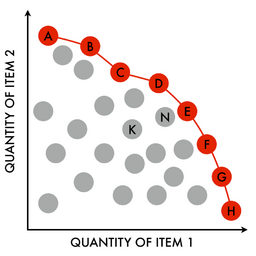
Definition

The Pareto frontier, P(Y), may be more formally described as follows. Consider a system with function $f:X\to {\mathbb{ℝ}}^m$, where X is a compact set of feasible decisions in the metric space ${\mathbb{ℝ}}^n$, and Y is the feasible set of criterion vectors in ${\mathbb{ℝ}}^m$, such that $Y=\{y\in {\mathbb{ℝ}}^m:y=f(x),x\in X\}$.

We assume that the preferred directions of criteria values are known. A point $y^{\prime \prime }\in {\mathbb{ℝ}}^m$ is preferred to (strictly dominates) another point $y^{\prime }\in {\mathbb{ℝ}}^m$, written as $y^{\prime \prime }\succ y^{\prime }$. The Pareto frontier is thus written as:

$P(Y)=\{y^{\prime }\in Y:\{y^{\prime \prime }\in Y:y^{\prime \prime }\succ y^{\prime },y^{\prime }\ne y^{\prime \prime }\}=\mathrm{\varnothing }\}.$

Marginal rate of substitution

A significant aspect of the Pareto frontier in economics is that, at a Pareto-efficient allocation, the marginal rate of substitution is the same for all consumers. A formal statement can be derived by considering a system with m consumers and n goods, and a utility function of each consumer as $z_i=f^i(x^i)$ where $x^i=(x_1^i,x_2^i,\dots ,x_n^i)$ is the vector of goods, both for all i. The feasibility constraint is $\sum _{i=1}^m{x}_j^i=b_j$ for $j=1,\dots ,n$. To find the Pareto optimal allocation, we maximize the Lagrangian:

$L_i((x_j^k{)}_{k,j},({\lambda }_k{)}_k,({\mu }_j{)}_j)=f^i(x^i)+\sum _{k=2}^m{\lambda }_k(z_k-f^k(x^k))+\sum _{j=1}^n{\mu }_j(b_j-\sum _{k=1}^m{x}_j^k)$

where $({\lambda }_k{)}_k$ and $({\mu }_j{)}_j$ are the vectors of multipliers. Taking the partial derivative of the Lagrangian with respect to each good $x_j^k$ for $j=1,\dots ,n$ and $k=1,\dots ,m$ gives the following system of first-order conditions:

$\frac{\partial L_i}{\partial x_j^i}=f_{x_j^i}^1-{\mu }_j=0\text{ for }j=1,\dots ,n,$

$\frac{\partial L_i}{\partial x_j^k}=-{\lambda }_k{f}_{x_j^k}^i-{\mu }_j=0\text{ for }k=2,\dots ,m\text{ and }j=1,\dots ,n,$

where $f_{x_j^i}$ denotes the partial derivative of $f$ with respect to $x_j^i$. Now, fix any $k\ne i$ and $j,s\in \{1,\dots ,n\}$. The above first-order condition imply that

$\frac{f_{x_j^i}^i}{f_{x_s^i}^i}=\frac{{\mu }_j}{{\mu }_s}=\frac{f_{x_j^k}^k}{f_{x_s^k}^k}.$

Computation

Algorithms for computing the Pareto frontier of a finite set of alternatives have been studied in computer science and power engineering. They include:

• "The maxima of a point set"
• "The maximum vector problem" or the skyline query
• "The scalarization algorithm" or the method of weighted sums
• "The $ϵ$-constraints method"
• Multi-objective Evolutionary Algorithms

Approximations

Since generating the entire Pareto front is often computationally-hard, there are algorithms for computing an approximate Pareto-front. For example, Legriel et al. call a set S an ε-approximation of the Pareto-front P, if the directed Hausdorff distance between S and P is at most ε. They observe that an ε-approximation of any Pareto front P in d dimensions can be found using (1/ε)^d queries.

Zitzler, Knowles and Thiele compare several algorithms for Pareto-set approximations on various criteria, such as invariance to scaling, monotonicity, and computational complexity.