Engineering:Strehl ratio
The Strehl ratio is a measure of the quality of optical image formation, originally proposed by Karl Strehl, after whom the term is named.[1][2] Used variously in situations where optical resolution is compromised due to lens aberrations or due to imaging through the turbulent atmosphere, the Strehl ratio has a value between 0 and 1, with a hypothetical, perfectly unaberrated optical system having a Strehl ratio of 1.
Mathematical definition
The Strehl ratio [math]\displaystyle{ S }[/math] is frequently defined[3] as the ratio of the peak aberrated image intensity from a point source compared to the maximum attainable intensity using an ideal optical system limited only by diffraction over the system's aperture. It is also often expressed in terms not of the peak intensity but the intensity at the image center (intersection of the optical axis with the focal plane) due to an on-axis source; in most important cases these definitions result in a very similar figure (or identical figure, when the point of peak intensity must be exactly at the center due to symmetry). Using the latter definition, the Strehl ratio [math]\displaystyle{ S }[/math] can be computed in terms of the wavefront-error [math]\displaystyle{ \delta(x,y) }[/math]: the offset of the wavefront due to an on-axis point source, compared to that produced by an ideal focusing system over the aperture A(x,y). Using Fraunhofer diffraction theory, one computes the wave amplitude using the Fourier transform of the aberrated pupil function evaluated at 0,0 (center of the image plane) where the phase factors of the Fourier transform formula are reduced to unity. Since the Strehl ratio refers to intensity, it is found from the squared magnitude of that amplitude:
- [math]\displaystyle{ S = |\langle e^{i\phi} \rangle|^2 = |\langle e^{i2\pi\delta/\lambda} \rangle|^2 }[/math]
where i is the imaginary unit, [math]\displaystyle{ \phi =2\pi\delta/\lambda }[/math] is the phase error over the aperture at wavelength λ, and the average of the complex quantity inside the brackets is taken over the aperture A(x,y).
The Strehl ratio can be estimated using only the statistics of the phase deviation [math]\displaystyle{ \phi }[/math], according to a formula rediscovered by Mahajan[4][5] but known long before in antenna theory as the Ruze formula[6]
- [math]\displaystyle{ S \approx {e^{-\sigma^2}} }[/math]
where sigma (σ) is the root mean square deviation over the aperture of the wavefront phase: [math]\displaystyle{ \sigma^2 = \langle (\phi - \bar\phi)^2 \rangle }[/math].
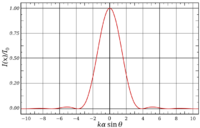
The Airy disk
Due to diffraction, even a focusing system which is perfect according to geometrical optics will have a limited spatial resolution. In the usual case of a uniform circular aperture, the point spread function (PSF) which describes the image formed from an object with no spatial extent (a "point source"), is given by the Airy disk as illustrated here. For a circular aperture, the peak intensity found at the center of the Airy disk defines the point source image intensity required for a Strehl ratio of unity. An imperfect optical system using the same physical aperture will generally produce a broader PSF in which the peak intensity is reduced according to the factor given by the Strehl ratio. An optical system with only minor imperfections in this sense may be referred to as "diffraction limited" as its PSF closely resembles the Airy disk; a Strehl ratio of greater than .8 is frequently cited as a criterion for the use of that designation.
Note that for a given aperture the size of the Airy disk grows linearly with the wavelength [math]\displaystyle{ \lambda }[/math], and consequently the peak intensity falls according to [math]\displaystyle{ \lambda^{-2} }[/math] so that the reference point for unity Strehl ratio is changed. Typically, as wavelength is increased, an imperfect optical system will have a broader PSF with a decreased peak intensity. However the peak intensity of the reference Airy disk would have decreased even more at that longer wavelength, resulting in a better Strehl ratio at longer wavelengths (typically) even though the actual image resolution is poorer.
Usage
The ratio is commonly used to assess the quality of astronomical seeing in the presence of atmospheric turbulence and assess the performance of any adaptive optical correction system. It is also used for the selection of short exposure images in the lucky imaging method.
In industry, the Strehl ratio has become a popular way to summarize the performance of an optical design because it gives the performance of a real system, of finite cost and complexity, relative to a theoretically perfect system, which would be infinitely expensive and complex to build and would still have a finite point spread function. It provides a simple method to decide whether a system with a Strehl ratio of, for example, 0.95 is good enough, or whether twice as much should be spent to try to get a Strehl ratio of perhaps 0.97 or 0.98.
Limitations
Characterizing the form of the point-spread function by a single number, as the Strehl Ratio does, will be meaningful and sensible only if the point-spread function is little distorted from its ideal (aberration-free) form, which will be true for a well-corrected system that operates close to the diffraction limit. That includes most telescopes and microscopes, but excludes most photographic systems, for example. The Strehl ratio has been linked via the work of André Maréchal[7] to an aberration tolerancing theory which is very useful to designers of well-corrected optical systems, allowing a meaningful link between the aberrations of geometrical optics and the diffraction theory of physical optics. A significant shortcoming of the Strehl ratio as a method of image assessment is that, although it is relatively easy to calculate for an optical design prescription on paper, it is normally difficult to measure for a real optical system, not least because the theoretical maximum peak intensity is not readily available.
See also
- Circle of confusion
- Fraunhofer diffraction
- Fraunhofer diffraction (mathematics)
- Huygens–Fresnel principle
- Optical transfer function
References
- ↑ Strehl, K. 1895, Aplanatische und fehlerhafte Abbildung im Fernrohr, Zeitschrift für Instrumentenkunde 15 (Oct.), 362-370.
- ↑ Strehl, K. 1902, Über Luftschlieren und Zonenfehler, Zeitschrift für Instrumentenkunde, 22 (July), 213-217. [PDF file]
- ↑ Sacek, Vladimir (July 14, 2006), "6.5. Strehl ratio", Notes on amateur telescope optics, http://www.telescope-optics.net/Strehl.htm, retrieved March 2, 2011
- ↑ Mahajan, Virendra (1983), "Strehl ratio for primary aberrations in terms of their aberration variance", J. Opt. Soc. Am. 73 (6): 860–861, doi:10.1364/JOSA.73.000860, http://www.opticsinfobase.org/josa/abstract.cfm?uri=josa-73-6-860
- ↑ "Strehl Ratio Formula - Wolfram|Alpha". Archived from the original on 2011-07-18. https://web.archive.org/web/20110718080036/http://www.wolframalpha.com/entities/calculators/Strehl_ratio_formula/av/uo/vo/. Retrieved 2011-03-03. Strehl ratio formula
- ↑ Kiedron, K.; Chian, C. T.; Chuang, K.L. (October–December 1986). "Statistical Analysis of the 70 Meter Antenna Surface Distortions". TDA Progress Report 42-88. http://tmo.jpl.nasa.gov/progress_report/42-88/88E.PDF.
- ↑ Maréchal André (1947). "Etude des effets combinés de la diffraction et des aberrations géométriques sur l'image d'un point lumineux". Rev. Opt. 2: 257–277.
External links
- Discussion page R.F. Royce' explanation of Strehl ratio in lay terms
- Strehl meter W.M. Keck Observatory Strehl calculator page
- Definition page Eric Weisstein's World of Physics
- Strehl ratio Telescope Optics Net practical explanation of Strehl ratio for amateur telescope makers
 |  |
