Physics:Irradiance
In radiometry, irradiance is the radiant flux received by a surface per unit area. The SI unit of irradiance is the watt per square metre (symbol W⋅m−2 or W/m2). The CGS unit erg per square centimetre per second (erg⋅cm−2⋅s−1) is often used in astronomy. Irradiance is often called intensity, but this term is avoided in radiometry where such usage leads to confusion with radiant intensity. In astrophysics, irradiance is called radiant flux.[1]
Spectral irradiance is the irradiance of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The two forms have different dimensions and units: spectral irradiance of a frequency spectrum is measured in watts per square metre per hertz (W⋅m−2⋅Hz−1), while spectral irradiance of a wavelength spectrum is measured in watts per square metre per metre (W⋅m−3), or more commonly watts per square metre per nanometre (W⋅m−2⋅nm−1).
Mathematical definitions
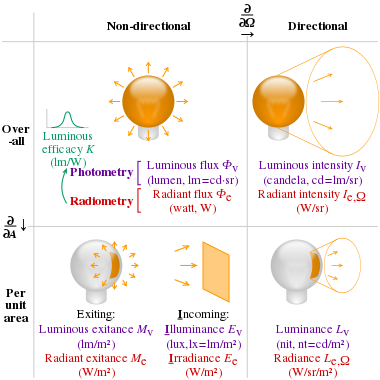
Irradiance
Irradiance of a surface, denoted Ee ("e" for "energetic", to avoid confusion with photometric quantities), is defined as[2]
where
- ∂ is the partial derivative symbol;
- Φe is the radiant flux received;
- A is the area.
The radiant flux emitted by a surface is called radiant exitance.
Spectral irradiance
Spectral irradiance in frequency of a surface, denoted Ee,ν, is defined as[2]
where ν is the frequency.
Spectral irradiance in wavelength of a surface, denoted Ee,λ, is defined as[2]
where λ is the wavelength.
Property
Irradiance of a surface is also, according to the definition of radiant flux, equal to the time-average of the component of the Poynting vector perpendicular to the surface:
where
- ⟨ • ⟩ is the time-average;
- S is the Poynting vector;
- α is the angle between a unit vector normal to the surface and S.
For a propagating sinusoidal linearly polarized electromagnetic plane wave, the Poynting vector always points to the direction of propagation while oscillating in magnitude. The irradiance of a surface is then given by[3]
where
- Em is the amplitude of the wave's electric field;
- n is the refractive index of the medium of propagation;
- c is the speed of light in vacuum;
- μ0 is the vacuum permeability;
- ε0 is the vacuum permittivity;
- is the impedance of free space.
This formula assumes that the magnetic susceptibility is negligible; i.e. that μr ≈ 1 (μ ≈ μ0) where μr is the relative magnetic permeability of the propagation medium. This assumption is typically valid in transparent media in the optical frequency range.
Point source
A point source of light produces spherical wavefronts. The irradiance in this case varies inversely with the square of the distance from the source.
where
- r is the distance;
- P is the radiant flux;
- A is the surface area of a sphere of radius r.
For quick approximations, this equation indicates that doubling the distance reduces irradiation to one quarter; or similarly, to double irradiation, reduce the distance to 71%.
In astronomy, stars are routinely treated as point sources even though they are much larger than the Earth. This is a good approximation because the distance from even a nearby star to the Earth is much larger than the star's diameter. For instance, the irradiance of Alpha Centauri A (radiant flux: 1.5 L☉, distance: 4.34 ly) is about 2.7 × 10−8 W/m2 on Earth.
Solar irradiance
The global irradiance on a horizontal surface on Earth consists of the direct irradiance Ee,dir and diffuse irradiance Ee,diff. On a tilted plane, there is another irradiance component, Ee,refl, which is the component that is reflected from the ground. The average ground reflection is about 20% of the global irradiance. Hence, the irradiance Ee on a tilted plane consists of three components:[4]
The integral of solar irradiance over a time period is called "solar exposure" or "insolation".[4][5]
Average solar irradiance at the top of the Earth's atmosphere is roughly 1361 W/m2, but at surface irradiance is approximately 1000 W/m2 on a clear day.
SI radiometry units
| Quantity | Unit | Dimension | Notes | |||||
|---|---|---|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol | ||||
| Radiant energy | Qe[nb 2] | joule | J | M⋅L2⋅T−2 | Energy of electromagnetic radiation. | |||
| Radiant energy density | we | joule per cubic metre | J/m3 | M⋅L−1⋅T−2 | Radiant energy per unit volume. | |||
| Radiant flux | Φe[nb 2] | watt | W = J/s | M⋅L2⋅T−3 | Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called "radiant power". | |||
| Spectral flux | Φe,ν[nb 3] | watt per hertz | W/Hz | M⋅L2⋅T−2 | Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅nm−1. | |||
| Φe,λ[nb 4] | watt per metre | W/m | M⋅L⋅T−3 | |||||
| Radiant intensity | Ie,Ω[nb 5] | watt per steradian | W/sr | M⋅L2⋅T−3 | Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity. | |||
| Spectral intensity | Ie,Ω,ν[nb 3] | watt per steradian per hertz | W⋅sr−1⋅Hz−1 | M⋅L2⋅T−2 | Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅nm−1. This is a directional quantity. | |||
| Ie,Ω,λ[nb 4] | watt per steradian per metre | W⋅sr−1⋅m−1 | M⋅L⋅T−3 | |||||
| Radiance | Le,Ω[nb 5] | watt per steradian per square metre | W⋅sr−1⋅m−2 | M⋅T−3 | Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called "intensity". | |||
| Spectral radiance | Le,Ω,ν[nb 3] | watt per steradian per square metre per hertz | W⋅sr−1⋅m−2⋅Hz−1 | M⋅T−2 | Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅m−2⋅nm−1. This is a directional quantity. This is sometimes also confusingly called "spectral intensity". | |||
| Le,Ω,λ[nb 4] | watt per steradian per square metre, per metre | W⋅sr−1⋅m−3 | M⋅L−1⋅T−3 | |||||
| Irradiance Flux density |
Ee[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux received by a surface per unit area. This is sometimes also confusingly called "intensity". | |||
| Spectral irradiance Spectral flux density |
Ee,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Irradiance of a surface per unit frequency or wavelength. This is sometimes also confusingly called "spectral intensity". Non-SI units of spectral flux density include jansky (1 Jy = 10−26 W⋅m−2⋅Hz−1) and solar flux unit (1 sfu = 10−22 W⋅m−2⋅Hz−1 = 104 Jy). | |||
| Ee,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiosity | Je[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called "intensity". | |||
| Spectral radiosity | Je,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. This is sometimes also confusingly called "spectral intensity". | |||
| Je,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiant exitance | Me[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. "Radiant emittance" is an old term for this quantity. This is sometimes also confusingly called "intensity". | |||
| Spectral exitance | Me,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. "Spectral emittance" is an old term for this quantity. This is sometimes also confusingly called "spectral intensity". | |||
| Me,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiant exposure | He | joule per square metre | J/m2 | M⋅T−2 | Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called "radiant fluence". | |||
| Spectral exposure | He,ν[nb 3] | joule per square metre per hertz | J⋅m−2⋅Hz−1 | M⋅T−1 | Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m−2⋅nm−1. This is sometimes also called "spectral fluence". | |||
| He,λ[nb 4] | joule per square metre, per metre | J/m3 | M⋅L−1⋅T−2 | |||||
| Hemispherical emissivity | ε | N/A | 1 | Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Spectral hemispherical emissivity | εν or ελ |
N/A | 1 | Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Directional emissivity | εΩ | N/A | 1 | Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface. | ||||
| Spectral directional emissivity | εΩ,ν or εΩ,λ |
N/A | 1 | Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Hemispherical absorptance | A | N/A | 1 | Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with "absorbance". | ||||
| Spectral hemispherical absorptance | Aν or Aλ |
N/A | 1 | Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with "spectral absorbance". | ||||
| Directional absorptance | AΩ | N/A | 1 | Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with "absorbance". | ||||
| Spectral directional absorptance | AΩ,ν or AΩ,λ |
N/A | 1 | Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with "spectral absorbance". | ||||
| Hemispherical reflectance | R | N/A | 1 | Radiant flux reflected by a surface, divided by that received by that surface. | ||||
| Spectral hemispherical reflectance | Rν or Rλ |
N/A | 1 | Spectral flux reflected by a surface, divided by that received by that surface. | ||||
| Directional reflectance | RΩ | N/A | 1 | Radiance reflected by a surface, divided by that received by that surface. | ||||
| Spectral directional reflectance | RΩ,ν or RΩ,λ |
N/A | 1 | Spectral radiance reflected by a surface, divided by that received by that surface. | ||||
| Hemispherical transmittance | T | N/A | 1 | Radiant flux transmitted by a surface, divided by that received by that surface. | ||||
| Spectral hemispherical transmittance | Tν or Tλ |
N/A | 1 | Spectral flux transmitted by a surface, divided by that received by that surface. | ||||
| Directional transmittance | TΩ | N/A | 1 | Radiance transmitted by a surface, divided by that received by that surface. | ||||
| Spectral directional transmittance | TΩ,ν or TΩ,λ |
N/A | 1 | Spectral radiance transmitted by a surface, divided by that received by that surface. | ||||
| Hemispherical attenuation coefficient | μ | reciprocal metre | m−1 | L−1 | Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Spectral hemispherical attenuation coefficient | μν or μλ |
reciprocal metre | m−1 | L−1 | Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Directional attenuation coefficient | μΩ | reciprocal metre | m−1 | L−1 | Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Spectral directional attenuation coefficient | μΩ,ν or μΩ,λ |
reciprocal metre | m−1 | L−1 | Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| See also: SI · Radiometry · Photometry | ||||||||
- ↑ Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
- ↑ 2.0 2.1 2.2 2.3 2.4 Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant exitance.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Spectral quantities given per unit frequency are denoted with suffix "ν" (Greek)—not to be confused with suffix "v" (for "visual") indicating a photometric quantity.
- ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 Spectral quantities given per unit wavelength are denoted with suffix "λ" (Greek).
- ↑ 5.0 5.1 Directional quantities are denoted with suffix "Ω" (Greek).

See also
- Albedo
- Fluence
- Illuminance
- Insolation
- Light diffusion
- PI curve (photosynthesis-irradiance curve)
- Solar azimuth angle
- Solar irradiance
- Solar noon
- Spectral flux density
- Stefan–Boltzmann law
References
- ↑ Carroll, Bradley W. (2017-09-07). An introduction to modern astrophysics. Cambridge University Press. p. 60. ISBN 978-1-108-42216-1. OCLC 991641816.
- ↑ 2.0 2.1 2.2 "Thermal insulation — Heat transfer by radiation — Physical quantities and definitions". ISO 9288:1989. ISO catalogue. 1989. https://www.iso.org/iso/home/store/catalogue_tc/catalogue_detail.htm?csnumber=16943.
- ↑ Griffiths, David J. (1999). Introduction to electrodynamics (3. ed., reprint. with corr. ed.). Upper Saddle River, NJ [u.a.]: Prentice-Hall. ISBN 0-13-805326-X. https://archive.org/details/introductiontoel00grif_0.
- ↑ 4.0 4.1 Quaschning, Volker (2003). "Technology fundamentals—The sun as an energy resource". Renewable Energy World 6 (5): 90–93. https://www.volker-quaschning.de/articles/fundamentals1/index_e.html.
- ↑ Liu, B. Y. H.; Jordan, R. C. (1960). "The interrelationship and characteristic distribution of direct, diffuse and total solar radiation". Solar Energy 4 (3): 1. doi:10.1016/0038-092X(60)90062-1. Bibcode: 1960SoEn....4....1L.
 |
