Eodermdrome
An eodermdrome is a form of word play wherein a word (or phrase) is formed from a set of letters (or words) in such a way that it has a non-planar spelling net. Gary S. Bloom, Allan Gewirtz, John W. Kennedy, and Peter J. Wexler first described the eodermdrome in May 1980,[1] and it subsequently became more widely known after publication in Word Ways: The Journal of Recreational Linguistics in August 1980.[2] It is well illustrated by the word eodermdrome itself. Eodermdrome contains only the letters e, o, d, r and m. When plotted as a graph, the lettered vertices are sequentially connected by edges to spell a word. If the graph is non-planar, the word is an eodermdrome. The graph of eodermdrome is the non-planar graph K5.
Eckler searched for all eodermdromes in Webster's Dictionary.[3] One of his examples is supersaturates. The graph of the complete word contains a subgraph which is a subdivision of the non-planar graph K3,3, and as such is itself non-planar.
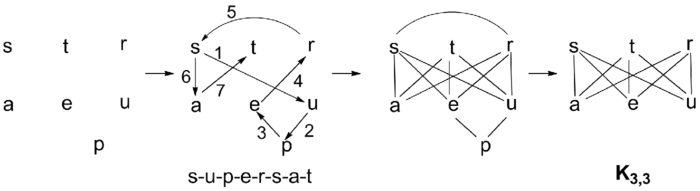
By extension, the vertices can be identified with words instead of letters to form eodermdromic phrases or sentences.
The concept has been studied within both mathematics and linguistics.[4][5]
See also
- Graph theory
- Kuratowski's theorem
- Palindrome
References
- ↑ Bloom, Gary S.; Gewirtz, Allan; Kennedy, John W.; Wexler, Peter J. (1981). "Eodermdromes: A Graph-Theoretical Tool for Linguistics". 4th International Conference on the Theory and Applications of Graphs, Western Michigan University, Kalamazoo, Michigan, May 6-9, 1980. pp. 81–94. ISBN 978-0-471-08473-0. OCLC 7171840.
- ↑ Bloom, Gary S.; Kennedy, John W.; Wexler, Peter J. (August 1980). "Ensnaring the Elusive Eodermdrome". Word Ways 13 (3): 131–140. http://digitalcommons.butler.edu/wordways/vol13/iss3/2/.
- ↑ Eckler, A. Ross (August 1980). "Dictionary Eodermdromes". Word Ways 13 (3): 141–146. http://digitalcommons.butler.edu/wordways/vol13/iss3/3/.
- ↑ Bloom, Gary S.; Kennedy, John W.; Quintas, Louis V. (1983). On Crossing Numbers and Linguistic Structures. Lecture Notes in Mathematics. 1018. pp. 14–22. doi:10.1007/BFb0071606. ISBN 978-3-540-12687-4.
- ↑ Kennedy, John W.; Wexler, Peter J.; Bloom, Gary S. (1980). "Linguistic Complexity and Minimal Eodermdromes". Linguistics 18 (1–2): 3–16. doi:10.1515/ling.1980.18.1-2.3. http://www.degruyter.com/view/j/ling.1980.18.issue-1-2/ling.1980.18.1-2.3/ling.1980.18.1-2.3.xml?rskey=u3xXnn&result=1.
 |  |
