Equation xy = yx

Short description: none

Graph of x^y = y^x. The line and curve intersect at (e, e).

In general, exponentiation fails to be commutative. However, the equation [math]\displaystyle{ x^y = y^x }[/math] has solutions, such as [math]\displaystyle{ x=2,\ y=4. }[/math]

History

The equation [math]\displaystyle{ x^y=y^x }[/math] is mentioned in a letter of Bernoulli to Goldbach (29 June 1728). The letter contains a statement that when [math]\displaystyle{ x\ne y, }[/math] the only solutions in natural numbers are [math]\displaystyle{ (2, 4) }[/math] and [math]\displaystyle{ (4, 2), }[/math] although there are infinitely many solutions in rational numbers, such as [math]\displaystyle{ (\tfrac{27}{8}, \tfrac{9}{4}) }[/math] and [math]\displaystyle{ (\tfrac{9}{4}, \tfrac{27}{8}) }[/math]. The reply by Goldbach (31 January 1729) contains a general solution of the equation, obtained by substituting [math]\displaystyle{ y=vx. }[/math] A similar solution was found by Euler.

J. van Hengel pointed out that if [math]\displaystyle{ r, n }[/math] are positive integers with [math]\displaystyle{ r \geq 3 }[/math], then [math]\displaystyle{ r^{r+n} \gt (r+n)^r; }[/math] therefore it is enough to consider possibilities [math]\displaystyle{ x = 1 }[/math] and [math]\displaystyle{ x = 2 }[/math] in order to find solutions in natural numbers.

The problem was discussed in a number of publications. In 1960, the equation was among the questions on the William Lowell Putnam Competition, which prompted Alvin Hausner to extend results to algebraic number fields.

Positive real solutions

Main source:

Explicit form

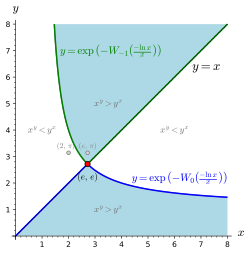
An infinite set of trivial solutions in positive real numbers is given by [math]\displaystyle{ x = y. }[/math] Nontrivial solutions can be written explicitly using the Lambert W function. The idea is to write the equation as [math]\displaystyle{ ae^b = c }[/math] and try to match [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math] by multiplying and raising both sides by the same value. Then apply the definition of the Lambert W function [math]\displaystyle{ a'e^{a'} = c' \Rightarrow a' = W(c') }[/math] to isolate the desired variable.

[math]\displaystyle{ \begin{align} y^x &= x^y = \exp\left(y\ln x\right) & \\ y^x \exp\left(-y\ln x\right) &= 1 & \left(\mbox{multiply by } \exp\left(-y\ln x\right)\right) \\ y\exp\left(-y\frac{\ln x}{x}\right) &= 1 & \left(\mbox{raise by } 1/x\right) \\ -y\frac{\ln x}{x}\exp\left(-y\frac{\ln x}{x}\right) &= \frac{-\ln x}{x} & \left(\mbox{multiply by } \frac{-\ln x}{x}\right) \end{align} }[/math]

[math]\displaystyle{ \Rightarrow -y\frac{\ln x}{x} = W\left(\frac{-\ln x}{x}\right) }[/math]

[math]\displaystyle{ \Rightarrow y = \frac{-x}{\ln x}\cdot W\left(\frac{-\ln x}{x}\right) = \exp\left(-W\left(\frac{-\ln x}{x}\right)\right) }[/math]

Where in the last step we used the identity [math]\displaystyle{ W(x)/x = \exp(-W(x)) }[/math].

Here we split the solution into the two branches of the Lambert W function and focus on each interval of interest, applying the identities:

[math]\displaystyle{ \begin{align} W_0\left(\frac{-\ln x}{x}\right) &= -\ln x \quad&\text{for } &0 \lt x \le e, \\ W_{-1}\left(\frac{-\ln x}{x}\right) &= -\ln x \quad&\text{for } &x \ge e. \end{align} }[/math]

• [math]\displaystyle{ 0 \lt x \le 1 }[/math]:

[math]\displaystyle{ \Rightarrow \frac{-\ln x}{x} \ge 0 }[/math]

[math]\displaystyle{ \begin{align}\Rightarrow y &= \exp\left(-W_0\left(\frac{-\ln x}{x}\right)\right) \\ &= \exp\left(-(-\ln x)\right) \\ &= x \end{align} }[/math]

• [math]\displaystyle{ 1 \lt x \lt e }[/math]:

[math]\displaystyle{ \Rightarrow \frac{-1}{e} \lt \frac{-\ln x}{x} \lt 0 }[/math]

[math]\displaystyle{ \Rightarrow y = \begin{cases} \exp\left(-W_0\left(\frac{-\ln x}{x}\right)\right) = x \\ \exp\left(-W_{-1}\left(\frac{-\ln x}{x}\right)\right) \end{cases} }[/math]

• [math]\displaystyle{ x = e }[/math]:

[math]\displaystyle{ \Rightarrow \frac{-\ln x}{x} = \frac{-1}{e} }[/math]

[math]\displaystyle{ \Rightarrow y = \begin{cases} \exp\left(-W_0\left(\frac{-\ln x}{x}\right)\right) = x \\ \exp\left(-W_{-1}\left(\frac{-\ln x}{x}\right)\right) = x \end{cases} }[/math]

• [math]\displaystyle{ x \gt e }[/math]:

[math]\displaystyle{ \Rightarrow \frac{-1}{e} \lt \frac{-\ln x}{x} \lt 0 }[/math]

[math]\displaystyle{ \Rightarrow y = \begin{cases} \exp\left(-W_0\left(\frac{-\ln x}{x}\right)\right) \\ \exp\left(-W_{-1}\left(\frac{-\ln x}{x}\right)\right) = x \end{cases} }[/math]

Hence the non-trivial solutions are:

[math]\displaystyle{ y = \begin{cases} \exp\left(-W_0\left(\frac{-\ln(x)}{x}\right)\right) \quad &\text{for } x \gt e,\\ \exp\left(-W_{-1}\left(\frac{-\ln x}{x}\right)\right) \quad &\text{for } 1 \lt x \lt e. \end{cases} }[/math]

Parametric form

Nontrivial solutions can be more easily found by assuming [math]\displaystyle{ x \ne y }[/math] and letting [math]\displaystyle{ y = vx. }[/math] Then

[math]\displaystyle{ (vx)^x = x^{vx} = (x^v)^x. }[/math]

Raising both sides to the power [math]\displaystyle{ \tfrac{1}{x} }[/math] and dividing by [math]\displaystyle{ x }[/math], we get

[math]\displaystyle{ v = x^{v-1}. }[/math]

Then nontrivial solutions in positive real numbers are expressed as the parametric equation

[math]\displaystyle{ \begin{align}x &= v^{1/(v-1)}, \\ y &= v^{v/(v-1)}.\end{align} }[/math]

The full solution thus is [math]\displaystyle{ (y=x) \cup \left(v^{1/(v-1)},v^{v/(v-1)}\right) \text{ for } v \gt 0, v \neq 1 . }[/math]

Based on the above solution, the derivative [math]\displaystyle{ dy/dx }[/math] is [math]\displaystyle{ 1 }[/math] for the [math]\displaystyle{ (x,y) }[/math] pairs on the line [math]\displaystyle{ y=x, }[/math] and for the other [math]\displaystyle{ (x,y) }[/math] pairs can be found by [math]\displaystyle{ (dy/dv)/(dx/dv), }[/math] which straightforward calculus gives as:

[math]\displaystyle{ \frac{dy}{dx} = v^2\left(\frac{v-1-\ln v}{v-1-v\ln v}\right) }[/math]

for [math]\displaystyle{ v \gt 0 }[/math] and [math]\displaystyle{ v \neq 1. }[/math]

Setting [math]\displaystyle{ v=2 }[/math] or [math]\displaystyle{ v=\tfrac{1}{2} }[/math] generates the nontrivial solution in positive integers, [math]\displaystyle{ 4^2=2^4. }[/math]

Other pairs consisting of algebraic numbers exist, such as [math]\displaystyle{ \sqrt 3 }[/math] and [math]\displaystyle{ 3\sqrt 3 }[/math], as well as [math]\displaystyle{ \sqrt[3]4 }[/math] and [math]\displaystyle{ 4\sqrt[3]4 }[/math].

The parameterization above leads to a geometric property of this curve. It can be shown that [math]\displaystyle{ x^y = y^x }[/math] describes the isocline curve where power functions of the form [math]\displaystyle{ x^v }[/math] have slope [math]\displaystyle{ v^2 }[/math] for some positive real choice of [math]\displaystyle{ v\neq 1 }[/math]. For example, [math]\displaystyle{ x^8=y }[/math] has a slope of [math]\displaystyle{ 8^2 }[/math] at [math]\displaystyle{ (\sqrt[7]{8}, \sqrt[7]{8}^8), }[/math] which is also a point on the curve [math]\displaystyle{ x^y=y^x. }[/math]

The trivial and non-trivial solutions intersect when [math]\displaystyle{ v = 1 }[/math]. The equations above cannot be evaluated directly at [math]\displaystyle{ v = 1 }[/math], but we can take the limit as [math]\displaystyle{ v\to 1 }[/math]. This is most conveniently done by substituting [math]\displaystyle{ v = 1 + 1/n }[/math] and letting [math]\displaystyle{ n\to\infty }[/math], so

[math]\displaystyle{ x = \lim_{v\to 1}v^{1/(v-1)} = \lim_{n\to\infty}\left(1+\frac 1n\right)^n = e. }[/math]

Thus, the line [math]\displaystyle{ y = x }[/math] and the curve for [math]\displaystyle{ x^y-y^x = 0,\,\, y \ne x }[/math] intersect at x = y = e.

As [math]\displaystyle{ x \to \infty }[/math], the nontrivial solution asymptotes to the line [math]\displaystyle{ y = 1 }[/math]. A more complete asymptotic form is

[math]\displaystyle{ y = 1 + \frac{\ln x}{x} + \frac{3}{2} \frac{(\ln x)^2}{x^2} + \cdots. }[/math]

Other real solutions

An infinite set of discrete real solutions with at least one of [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] negative also exist. These are provided by the above parameterization when the values generated are real. For example, [math]\displaystyle{ x=\frac{1}{\sqrt[3]{-2}} }[/math], [math]\displaystyle{ y=\frac{-2}{\sqrt[3]{-2}} }[/math] is a solution (using the real cube root of [math]\displaystyle{ -2 }[/math]). Similarly an infinite set of discrete solutions is given by the trivial solution [math]\displaystyle{ y=x }[/math] for [math]\displaystyle{ x\lt 0 }[/math] when [math]\displaystyle{ x^x }[/math] is real; for example [math]\displaystyle{ x=y=-1 }[/math].

Similar graphs

Equation ^x√y = ^y√x

The equation [math]\displaystyle{ \sqrt[x]y = \sqrt[y]x }[/math] produces a graph where the line and curve intersect at [math]\displaystyle{ 1/e }[/math]. The curve also terminates at (0, 1) and (1, 0), instead of continuing on to infinity.

The curved section can be written explicitly as

[math]\displaystyle{ y=e^{W_0(\ln(x^x))} \quad \mathrm{for} \quad 0\lt x\lt 1/e, }[/math]

[math]\displaystyle{ y=e^{W_{-1}(\ln(x^x))} \quad \mathrm{for} \quad 1/e\lt x\lt 1. }[/math]

This equation describes the isocline curve where power functions have slope 1, analogous to the geometric property of [math]\displaystyle{ x^y = y^x }[/math] described above.

The equation is equivalent to [math]\displaystyle{ y^y=x^x, }[/math] as can be seen by raising both sides to the power [math]\displaystyle{ xy. }[/math] Equivalently, this can also be shown to demonstrate that the equation [math]\displaystyle{ \sqrt[y]{y}=\sqrt[x]{x} }[/math] is equivalent to [math]\displaystyle{ x^y = y^x }[/math].

Equation log_x(y) = log_y(x)

The equation [math]\displaystyle{ \log_x(y) = \log_y(x) }[/math] produces a graph where the curve and line intersect at (1, 1). The curve becomes asymptotic to 0, as opposed to 1; it is, in fact, the positive section of y = 1/x.

External links

• "Rational Solutions to x^y = y^x". CTK Wiki Math. http://www.cut-the-knot.org/wiki-math/index.php?n=Algebra.RationalSolutionOfXYYX. 
• "x^y = y^x - commuting powers". Arithmetical and Analytical Puzzles. Torsten Sillke. https://www.math.uni-bielefeld.de/~sillke/PUZZLES/x%5Ey-x%5Ey. 
• dborkovitz (2012-01-29). "Parametric Graph of x^y=y^x". GeoGebra. http://www.geogebra.org/material/show/id/3940. 
• OEIS sequence A073084 (Decimal expansion of −x, where x is the negative solution to the equation 2^x = x^2)