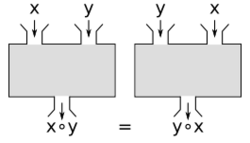
Commutative property
 | |
| Type | Property |
|---|---|
| Field | Algebra |
| Statement | A binary operation is commutative if changing the order of the operands does not change the result. |
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. "3 + 4 = 4 + 3" or "2 × 5 = 5 × 2", the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, "3 − 5 ≠ 5 − 3"); such operations are not commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many years implicitly assumed. Thus, this property was not named until the 19th century, when mathematics started to become formalized.[1][2] A similar property exists for binary relations; a binary relation is said to be symmetric if the relation applies regardless of the order of its operands; for example, equality is symmetric as two equal mathematical objects are equal regardless of their order.[3]
Mathematical definitions
A binary operation on a set S is called commutative if[4][5] In other words, an operation is commutative if every two elements commute. An operation that does not satisfy the above property is called noncommutative.
One says that x commutes with y or that x and y commute under if That is, a specific pair of elements may commute even if the operation is (strictly) noncommutative.
Examples
Commutative operations
- Addition and multiplication are commutative in most number systems, and, in particular, between natural numbers, integers, rational numbers, real numbers and complex numbers. This is also true in every field.
- Addition is commutative in every vector space and in every algebra.
- Union and intersection are commutative operations on sets.
- "And" and "or" are commutative logical operations.
Noncommutative operations
Some noncommutative binary operations:[6]
Division, subtraction, and exponentiation
Division is noncommutative, since .
Subtraction is noncommutative, since . However it is classified more precisely as anti-commutative, since .
Exponentiation is noncommutative, since . This property leads to two different "inverse" operations of exponentiation (namely, the nth-root operation and the logarithm operation), which is unlike the multiplication. [7]
Truth functions
Some truth functions are noncommutative, since the truth tables for the functions are different when one changes the order of the operands. For example, the truth tables for (A ⇒ B) = (¬A ∨ B) and (B ⇒ A) = (A ∨ ¬B) are
A B A ⇒ B B ⇒ A F F T T F T T F T F F T T T T T
Function composition of linear functions
Function composition of linear functions from the real numbers to the real numbers is almost always noncommutative. For example, let and . Then and This also applies more generally for linear and affine transformations from a vector space to itself (see below for the Matrix representation).
Matrix multiplication
Matrix multiplication of square matrices is almost always noncommutative, for example:
Vector product
The vector product (or cross product) of two vectors in three dimensions is anti-commutative; i.e., b × a = −(a × b).
History and etymology

Records of the implicit use of the commutative property go back to ancient times. The Egyptians used the commutative property of multiplication to simplify computing products.[8][9] Euclid is known to have assumed the commutative property of multiplication in his book Elements.[10] Formal uses of the commutative property arose in the late 18th and early 19th centuries, when mathematicians began to work on a theory of functions. Today the commutative property is a well-known and basic property used in most branches of mathematics.
The first recorded use of the term commutative was in a memoir by François Servois in 1814,[1][11] which used the word commutatives when describing functions that have what is now called the commutative property. The word is a combination of the French word commuter meaning "to substitute or switch" and the suffix -ative meaning "tending to" so the word literally means "tending to substitute or switch". The term then appeared in English in 1838.[2] in Duncan Farquharson Gregory's article entitled "On the real nature of symbolical algebra" published in 1840 in the Transactions of the Royal Society of Edinburgh.[12]
Propositional logic
| Transformation rules |
|---|
| Propositional calculus |
| Rules of inference |
| Rules of replacement |
| Predicate logic |
Rule of replacement
In truth-functional propositional logic, commutation,[13][14] or commutativity[15] refer to two valid rules of replacement. The rules allow one to transpose propositional variables within logical expressions in logical proofs. The rules are: and where "" is a metalogical symbol representing "can be replaced in a proof with".
Truth functional connectives
Commutativity is a property of some logical connectives of truth functional propositional logic. The following logical equivalences demonstrate that commutativity is a property of particular connectives. The following are truth-functional tautologies.
- Commutativity of conjunction
- Commutativity of disjunction
- Commutativity of implication (also called the law of permutation)
- Commutativity of equivalence (also called the complete commutative law of equivalence)
Set theory
In group and set theory, many algebraic structures are called commutative when certain operands satisfy the commutative property. In higher branches of mathematics, such as analysis and linear algebra the commutativity of well-known operations (such as addition and multiplication on real and complex numbers) is often used (or implicitly assumed) in proofs.[16][17][18]
Mathematical structures and commutativity
- A commutative semigroup is a set endowed with a total, associative and commutative operation.
- If the operation additionally has an identity element, we have a commutative monoid
- An abelian group, or commutative group is a group whose group operation is commutative.[17]
- A commutative ring is a ring whose multiplication is commutative. (Addition in a ring is always commutative.)[19]
- In a field both addition and multiplication are commutative.[20]
Related properties
Associativity
The associative property is closely related to the commutative property. The associative property of an expression containing two or more occurrences of the same operator states that the order operations are performed in does not affect the final result, as long as the order of terms does not change. In contrast, the commutative property states that the order of the terms does not affect the final result.
Most commutative operations encountered in practice are also associative. However, commutativity does not imply associativity. A counterexample is the function which is clearly commutative (interchanging x and y does not affect the result), but it is not associative (since, for example, but ). More such examples may be found in commutative non-associative magmas. Furthermore, associativity does not imply commutativity either – for example multiplication of quaternions or of matrices is always associative but not always commutative.
Distributive
Symmetry
Some forms of symmetry can be directly linked to commutativity. When a commutative operation is written as a binary function then this function is called a symmetric function, and its graph in three-dimensional space is symmetric across the plane . For example, if the function f is defined as then is a symmetric function.
For relations, a symmetric relation is analogous to a commutative operation, in that if a relation R is symmetric, then .
Non-commuting operators in quantum mechanics
In quantum mechanics as formulated by Schrödinger, physical variables are represented by linear operators such as (meaning multiply by ), and . These two operators do not commute as may be seen by considering the effect of their compositions and (also called products of operators) on a one-dimensional wave function :
According to the uncertainty principle of Heisenberg, if the two operators representing a pair of variables do not commute, then that pair of variables are mutually complementary, which means they cannot be simultaneously measured or known precisely. For example, the position and the linear momentum in the -direction of a particle are represented by the operators and , respectively (where is the reduced Planck constant). This is the same example except for the constant , so again the operators do not commute and the physical meaning is that the position and linear momentum in a given direction are complementary.
See also
- Anticommutative property
- Centralizer and normalizer (also called a commutant)
- Commutative diagram
- Commutative (neurophysiology)
- Commutator
- Parallelogram law
- Particle statistics (for commutativity in physics)
- Proof that Peano's axioms imply the commutativity of the addition of natural numbers
- Quasi-commutative property
- Trace monoid
- Commuting probability
Notes
- ↑ 1.0 1.1 Cabillón & Miller, Commutative and Distributive
- ↑ 2.0 2.1 Flood, Raymond; Rice, Adrian; Wilson, Robin, eds (2011). Mathematics in Victorian Britain. Oxford University Press. p. 4. ISBN 9780191627941. https://books.google.com/books?id=YruifIx88AQC&pg=PA4.
- ↑ Weisstein, Eric W.. "Symmetric Relation". http://mathworld.wolfram.com/SymmetricRelation.html.
- ↑ Krowne, p. 1
- ↑ Weisstein, Commute, p. 1
- ↑ Yark, p. 1
- ↑ "User MathematicalOrchid" (in en). https://math.stackexchange.com/users/29949/mathematicalorchid.
- ↑ Lumpkin 1997, p. 11
- ↑ Gay & Shute 1987
- ↑ O'Conner & Robertson Real Numbers
- ↑ O'Conner & Robertson, Servois
- ↑ Gregory, D. F. (1840). "On the real nature of symbolical algebra". Transactions of the Royal Society of Edinburgh 14: 208–216. https://archive.org/details/transactionsofro14royal.
- ↑ Moore and Parker
- ↑ Copi & Cohen 2005
- ↑ Hurley & Watson 2016
- ↑ Axler 1997, p. 2
- ↑ 17.0 17.1 Gallian 2006, p. 34
- ↑ Gallian 2006, pp. 26, 87
- ↑ Gallian 2006, p. 236
- ↑ Gallian 2006, p. 250
References
Books
- Axler, Sheldon (1997). Linear Algebra Done Right, 2e. Springer. ISBN 0-387-98258-2.
- Abstract algebra theory. Covers commutativity in that context. Uses property throughout book.
- Copi, Irving M.; Cohen, Carl (2005). Introduction to Logic (12th ed.). Prentice Hall. ISBN 9780131898349. https://archive.org/details/isbn_9780536179364.
- Gallian, Joseph (2006). Contemporary Abstract Algebra (6e ed.). Houghton Mifflin. ISBN 0-618-51471-6.
- Linear algebra theory. Explains commutativity in chapter 1, uses it throughout.
- Goodman, Frederick (2003). Algebra: Abstract and Concrete, Stressing Symmetry (2e ed.). Prentice Hall. ISBN 0-13-067342-0.
- Abstract algebra theory. Uses commutativity property throughout book.
- Hurley, Patrick J.; Watson, Lori (2016). A Concise Introduction to Logic (12th ed.). Cengage Learning. ISBN 978-1-337-51478-1. https://books.google.com/books?id=l-W5DQAAQBAJ&pg=PA675.
Articles
- Lumpkin, B. (1997). "The Mathematical Legacy of Ancient Egypt – A Response To Robert Palter". http://www.ethnomath.org/resources/lumpkin1997.pdf.
- Article describing the mathematical ability of ancient civilizations.
- Gay, Robins R.; Shute, Charles C. D. (1987). The Rhind Mathematical Papyrus: An Ancient Egyptian Text. British Museum. ISBN 0-7141-0944-4.
- Translation and interpretation of the Rhind Mathematical Papyrus.
Online resources
- Hazewinkel, Michiel, ed. (2001), "Commutativity", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=p/c023420
- Krowne, Aaron, Commutative at PlanetMath.org., Accessed 8 August 2007.
- Definition of commutativity and examples of commutative operations
- Weisstein, Eric W.. "Commute". http://mathworld.wolfram.com/Commute.html., Accessed 8 August 2007.
- Explanation of the term commute
- "Yark". http://planetmath.org/?op=getuser&id=2760. Examples of non-commutative operations at PlanetMath.org., Accessed 8 August 2007
- Examples proving some noncommutative operations
- O'Conner, J.J.; Robertson, E.F.. "History of real numbers". MacTutor. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Real_numbers_1.html.
- Article giving the history of the real numbers
- Cabillón, Julio; Miller, Jeff. "Earliest Known Uses of Mathematical Terms". http://jeff560.tripod.com/c.html.
- Page covering the earliest uses of mathematical terms
- O'Conner, J.J.; Robertson, E.F.. "biography of François Servois". MacTutor. http://www-groups.dcs.st-and.ac.uk/~history/Biographies/Servois.html.
- Biography of Francois Servois, who first used the term
 |
