Erdős–Mordell inequality

In Euclidean geometry, the Erdős–Mordell inequality states that for any triangle ABC and point P inside ABC, the sum of the distances from P to the sides is less than or equal to half of the sum of the distances from P to the vertices. It is named after Paul Erdős and Louis Mordell. (Erdős 1935) posed the problem of proving the inequality; a proof was provided two years later by Mordell and D. F. Barrow (1937). This solution was however not very elementary. Subsequent simpler proofs were then found by (Kazarinoff 1957), (Bankoff 1958), and (Alsina Nelsen). Barrow's inequality is a strengthened version of the Erdős–Mordell inequality in which the distances from P to the sides are replaced by the distances from P to the points where the angle bisectors of ∠APB, ∠BPC, and ∠CPA cross the sides. Although the replaced distances are longer, their sum is still less than or equal to half the sum of the distances to the vertices.

Statement

Erdős–Mordell inequality

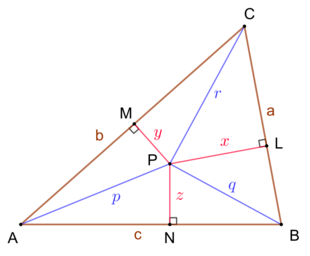
Let [math]\displaystyle{ P }[/math] be an arbitrary point P inside a given triangle [math]\displaystyle{ ABC }[/math], and let [math]\displaystyle{ PL }[/math], [math]\displaystyle{ PM }[/math], and [math]\displaystyle{ PN }[/math] be the perpendiculars from [math]\displaystyle{ P }[/math] to the sides of the triangles. (If the triangle is obtuse, one of these perpendiculars may cross through a different side of the triangle and end on the line supporting one of the sides.) Then the inequality states that

[math]\displaystyle{ PA+PB+PC\geq 2(PL+PM+PN) }[/math]

Proof

Let the sides of ABC be a opposite A, b opposite B, and c opposite C; also let PA = p, PB = q, PC = r, dist(P;BC) = x, dist(P;CA) = y, dist(P;AB) = z. First, we prove that

[math]\displaystyle{ cr\geq ax+by. }[/math]

This is equivalent to

[math]\displaystyle{ \frac{c(r+z)}2\geq \frac{ax+by+cz}2. }[/math]

The right side is the area of triangle ABC, but on the left side, r + z is at least the height of the triangle; consequently, the left side cannot be smaller than the right side. Now reflect P on the angle bisector at C. We find that cr ≥ ay + bx for P's reflection. Similarly, bq ≥ az + cx and ap ≥ bz + cy. We solve these inequalities for r, q, and p:

[math]\displaystyle{ r\geq (a/c)y+(b/c)x, }[/math]

[math]\displaystyle{ q\geq (a/b)z+(c/b)x, }[/math]

[math]\displaystyle{ p\geq (b/a)z+(c/a)y. }[/math]

Adding the three up, we get

[math]\displaystyle{ p + q + r \geq \left( \frac{b}{c} + \frac{c}{b} \right) x + \left( \frac{a}{c} + \frac{c}{a} \right) y + \left( \frac{a}{b} + \frac{b}{a} \right) z. }[/math]

Since the sum of a positive number and its reciprocal is at least 2 by AM–GM inequality, we are finished. Equality holds only for the equilateral triangle, where P is its centroid.

Another strengthened version

Let ABC be a triangle inscribed into a circle (O) and P be a point inside of ABC. Let D, E, F be the orthogonal projections of P onto BC, CA, AB. M, N, Q be the orthogonal projections of P onto tangents to (O) at A, B, C respectively, then:

[math]\displaystyle{ PM+PN+PQ \ge 2(PD+PE+PF) }[/math]

Equality hold if and only if triangle ABC is equilateral (Dao, Nguyen & Pham 2016; Marinescu & Monea 2017)

A generalization

Let [math]\displaystyle{ A_1A_2...A_n }[/math] be a convex polygon, and [math]\displaystyle{ P }[/math] be an interior point of [math]\displaystyle{ A_1A_2...A_n }[/math]. Let [math]\displaystyle{ R_i }[/math] be the distance from [math]\displaystyle{ P }[/math] to the vertex [math]\displaystyle{ A_i }[/math] , [math]\displaystyle{ r_i }[/math] the distance from [math]\displaystyle{ P }[/math] to the side [math]\displaystyle{ A_iA_{i+1} }[/math], [math]\displaystyle{ w_i }[/math] the segment of the bisector of the angle [math]\displaystyle{ A_iPA_{i+1} }[/math] from [math]\displaystyle{ P }[/math] to its intersection with the side [math]\displaystyle{ A_iA_{i+1} }[/math] then (Lenhard 1961):

[math]\displaystyle{ \sum_{i=1}^{n}R_i \ge \left(\sec{\frac{\pi}{n}}\right)\sum_{i=1}^{n} w_i \ge \left(\sec{\frac{\pi}{n}}\right)\sum_{i=1}^{n} r_i }[/math]

See also

• List of triangle inequalities

References

• Alsina, Claudi; Nelsen, Roger B. (2007), "A visual proof of the Erdős-Mordell inequality", Forum Geometricorum 7: 99–102, http://forumgeom.fau.edu/FG2007volume7/FG200711index.html .
• "An elementary proof of the Erdős-Mordell theorem", American Mathematical Monthly 65 (7): 521, 1958, doi:10.2307/2308580 .
• Dao, Thanh Oai; Nguyen, Tien Dung; Pham, Ngoc Mai (2016), "A strengthened version of the Erdős-Mordell inequality", Forum Geometricorum 16: 317–321, http://forumgeom.fau.edu/FG2016volume16/FG201638.pdf .
• "Problem 3740", American Mathematical Monthly 42: 396, 1935, doi:10.2307/2301373 .
• Kazarinoff, D. K. (1957), "A simple proof of the Erdős-Mordell inequality for triangles", Michigan Mathematical Journal 4 (2): 97–98, doi:10.1307/mmj/1028988998 .
• Lenhard, Hans-Christof (1961), "Verallgemeinerung und Verschärfung der Erdös-Mordellschen Ungleichung für Polygone", Archiv für Mathematische Logik und Grundlagenforschung 12: 311–314, doi:10.1007/BF01650566 .
• Marinescu, Dan Ștefan; Monea, Mihai (2017), "About a strengthened version of the Erdős-Mordell inequality", Forum Geometricorum 17: 197–202, http://forumgeom.fau.edu/FG2017volume17/FG201723.pdf .
• "Solution to 3740", American Mathematical Monthly 44: 252–254, 1937, doi:10.2307/2300713 .

External links

• Weisstein, Eric W.. "Erdős-Mordell Theorem". http://mathworld.wolfram.com/Erdos-MordellTheorem.html. 
• Alexander Bogomolny, "Erdös-Mordell Inequality", from Cut-the-Knot.