Inequality of arithmetic and geometric means

Short description: Arithmetic mean is greater than or equal to geometric mean

Visual proof that (x + y)² ≥ 4xy. Taking square roots and dividing by two gives the AM–GM inequality.

In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if every number in the list is the same (in which case they are both that number).

The simplest non-trivial case – i.e., with more than one variable – for two non-negative numbers x and y, is the statement that

[math]\displaystyle{ \frac{x+y}2 \ge \sqrt{xy} }[/math]

with equality if and only if x = y. This case can be seen from the fact that the square of a real number is always non-negative (greater than or equal to zero) and from the elementary case (a ± b)² = a² ± 2ab + b² of the binomial formula:

[math]\displaystyle{ \begin{align} 0 & \le (x-y)^2 \\ & = x^2-2xy+y^2 \\ & = x^2+2xy+y^2 - 4xy \\ & = (x+y)^2 - 4xy. \end{align} }[/math]

Hence (x + y)² ≥ 4xy, with equality precisely when (x − y)² = 0, i.e. x = y. The AM–GM inequality then follows from taking the positive square root of both sides and then dividing both sides by 2.

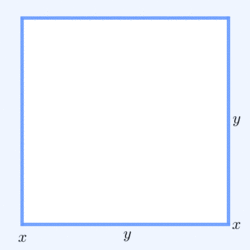
For a geometrical interpretation, consider a rectangle with sides of length x and y, hence it has perimeter 2x + 2y and area xy. Similarly, a square with all sides of length √xy has the perimeter 4√xy and the same area as the rectangle. The simplest non-trivial case of the AM–GM inequality implies for the perimeters that 2x + 2y ≥ 4√xy and that only the square has the smallest perimeter amongst all rectangles of equal area.

Extensions of the AM–GM inequality are available to include weights or generalized means.

Background

The arithmetic mean, or less precisely the average, of a list of n numbers x₁, x₂, . . . , x_n is the sum of the numbers divided by n:

[math]\displaystyle{ \frac{x_1 + x_2 + \cdots + x_n}{n}. }[/math]

The geometric mean is similar, except that it is only defined for a list of nonnegative real numbers, and uses multiplication and a root in place of addition and division:

[math]\displaystyle{ \sqrt[n]{x_1 \cdot x_2 \cdots x_n}. }[/math]

If x₁, x₂, . . . , x_n > 0, this is equal to the exponential of the arithmetic mean of the natural logarithms of the numbers:

[math]\displaystyle{ \exp \left( \frac{\ln {x_1} + \ln {x_2} + \cdots + \ln {x_n}}{n} \right). }[/math]

The inequality

Restating the inequality using mathematical notation, we have that for any list of n nonnegative real numbers x₁, x₂, . . . , x_n,

[math]\displaystyle{ \frac{x_1 + x_2 + \cdots + x_n}{n} \ge \sqrt[n]{x_1 \cdot x_2 \cdots x_n}\,, }[/math]

and that equality holds if and only if x₁ = x₂ = · · · = x_n.

Geometric interpretation

In two dimensions, 2x₁ + 2x₂ is the perimeter of a rectangle with sides of length x₁ and x₂. Similarly, 4√x₁x₂ is the perimeter of a square with the same area, x₁x₂, as that rectangle. Thus for n = 2 the AM–GM inequality states that a rectangle of a given area has the smallest perimeter if that rectangle is also a square.

The full inequality is an extension of this idea to n dimensions. Every vertex of an n-dimensional box is connected to n edges. If these edges' lengths are x₁, x₂, . . . , x_n, then x₁ + x₂ + · · · + x_n is the total length of edges incident to the vertex. There are 2ⁿ vertices, so we multiply this by 2ⁿ; since each edge, however, meets two vertices, every edge is counted twice. Therefore, we divide by 2 and conclude that there are 2ⁿ⁻¹n edges. There are equally many edges of each length and n lengths; hence there are 2ⁿ⁻¹ edges of each length and the total of all edge lengths is 2ⁿ⁻¹(x₁ + x₂ + · · · + x_n). On the other hand,

[math]\displaystyle{ 2^{n-1}(x_1+\ldots+x_n)= 2^{n-1} n \sqrt[n]{x_1 x_2 \cdots x_n} }[/math]

is the total length of edges connected to a vertex on an n-dimensional cube of equal volume, since in this case x₁=...=x_n. Since the inequality says

[math]\displaystyle{ {x_1 + x_2 +\cdots + x_n \over n} \ge \sqrt[n]{x_1 x_2\cdots x_n}, }[/math]

it can be restated by multiplying through by n2^n–1 to obtain

[math]\displaystyle{ 2^{n-1}(x_1 + x_2 + \cdots + x_n) \ge 2^{n-1} n \sqrt[n]{x_1 x_2\cdots x_n} }[/math]

with equality if and only if x₁ = x₂ = · · · = x_n.

Thus the AM–GM inequality states that only the n-cube has the smallest sum of lengths of edges connected to each vertex amongst all n-dimensional boxes with the same volume.

Examples

Example 1

If [math]\displaystyle{ a,b,c\gt 0 }[/math], then the A.M.-G.M. tells us that

[math]\displaystyle{ (1+a)(1+b)(1+c)\ge 8\sqrt{abc} }[/math]

Example 2

A simple upper bound for [math]\displaystyle{ n! }[/math] can be found. AM-GM tells us

[math]\displaystyle{ 1+2+\dots+n \ge n\sqrt[n]{n!} }[/math]

[math]\displaystyle{ \frac{n(n+1)}{2} \ge n\sqrt[n]{n!} }[/math]

and so

[math]\displaystyle{ \left(\frac{n+1}{2}\right)^n \ge n! }[/math]

with equality at [math]\displaystyle{ n=1 }[/math].

Equivalently,

[math]\displaystyle{ (n+1)^n \ge 2^nn! }[/math]

Example 3

Consider the function

[math]\displaystyle{ f(x,y,z) = \frac{x}{y} + \sqrt{\frac{y}{z}} + \sqrt[3]{\frac{z}{x}} }[/math]

for all positive real numbers x, y and z. Suppose we wish to find the minimal value of this function. It can be rewritten as:

[math]\displaystyle{ \begin{align} f(x,y,z) &= 6 \cdot \frac{ \frac{x}{y} + \frac{1}{2} \sqrt{\frac{y}{z}} + \frac{1}{2} \sqrt{\frac{y}{z}} + \frac{1}{3} \sqrt[3]{\frac{z}{x}} + \frac{1}{3} \sqrt[3]{\frac{z}{x}} + \frac{1}{3} \sqrt[3]{\frac{z}{x}} }{6}\\ &=6\cdot\frac{x_1+x_2+x_3+x_4+x_5+x_6}{6} \end{align} }[/math]

with

[math]\displaystyle{ x_1=\frac{x}{y},\qquad x_2=x_3=\frac{1}{2} \sqrt{\frac{y}{z}},\qquad x_4=x_5=x_6=\frac{1}{3} \sqrt[3]{\frac{z}{x}}. }[/math]

Applying the AM–GM inequality for n = 6, we get

[math]\displaystyle{ \begin{align} f(x,y,z) &\ge 6 \cdot \sqrt[6]{ \frac{x}{y} \cdot \frac{1}{2} \sqrt{\frac{y}{z}} \cdot \frac{1}{2} \sqrt{\frac{y}{z}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} \cdot \frac{1}{3} \sqrt[3]{\frac{z}{x}} }\\ &= 6 \cdot \sqrt[6]{ \frac{1}{2 \cdot 2 \cdot 3 \cdot 3 \cdot 3} \frac{x}{y} \frac{y}{z} \frac{z}{x} }\\ &= 2^{2/3} \cdot 3^{1/2}. \end{align} }[/math]

Further, we know that the two sides are equal exactly when all the terms of the mean are equal:

[math]\displaystyle{ f(x,y,z) = 2^{2/3} \cdot 3^{1/2} \quad \mbox{when} \quad \frac{x}{y} = \frac{1}{2} \sqrt{\frac{y}{z}} = \frac{1}{3} \sqrt[3]{\frac{z}{x}}. }[/math]

All the points (x, y, z) satisfying these conditions lie on a half-line starting at the origin and are given by

[math]\displaystyle{ (x,y,z)=\biggr(t,\sqrt[3]{2}\sqrt{3}\,t,\frac{3\sqrt{3}}{2}\,t\biggr)\quad\mbox{with}\quad t\gt 0. }[/math]

Applications

An important practical application in financial mathematics is to computing the rate of return: the annualized return, computed via the geometric mean, is less than the average annual return, computed by the arithmetic mean (or equal if all returns are equal). This is important in analyzing investments, as the average return overstates the cumulative effect.

Proofs of the AM–GM inequality

Proof using Jensen's inequality

Jensen's inequality states that the value of a concave function of an arithmetic mean is greater than or equal to the arithmetic mean of the function's values. Since the logarithm function is concave, we have

[math]\displaystyle{ \log \left(\frac { \sum_i x_i}{n} \right) \geq \sum \frac{1}{n} \log x_i = \sum \left( \log x_i^{1/n}\right) = \log \left( \prod x_i^{1/n}\right). }[/math]

Taking antilogs of the far left and far right sides, we have the AM–GM inequality.

Proof by successive replacement of elements

We have to show that

[math]\displaystyle{ \alpha = \frac{x_1+x_2+\cdots+x_n}{n} \ge \sqrt[n]{x_1x_2 \cdots x_n}=\beta }[/math]

with equality only when all numbers are equal.

If not all numbers are equal, then there exist [math]\displaystyle{ x_i,x_j }[/math] such that [math]\displaystyle{ x_i\lt \alpha\lt x_j }[/math]. Replacing x_i by [math]\displaystyle{ \alpha }[/math] and x_j by [math]\displaystyle{ (x_i+x_j-\alpha) }[/math] will leave the arithmetic mean of the numbers unchanged, but will increase the geometric mean because

[math]\displaystyle{ \alpha(x_j+x_i-\alpha)-x_ix_j=(\alpha-x_i)(x_j-\alpha)\gt 0 }[/math]

If the numbers are still not equal, we continue replacing numbers as above. After at most [math]\displaystyle{ (n-1) }[/math] such replacement steps all the numbers will have been replaced with [math]\displaystyle{ \alpha }[/math] while the geometric mean strictly increases at each step. After the last step, the geometric mean will be [math]\displaystyle{ \sqrt[n]{\alpha\alpha \cdots \alpha}=\alpha }[/math], proving the inequality.

It may be noted that the replacement strategy works just as well from the right hand side. If any of the numbers is 0 then so will the geometric mean thus proving the inequality trivially. Therefore we may suppose that all the numbers are positive. If they are not all equal, then there exist [math]\displaystyle{ x_i,x_j }[/math] such that [math]\displaystyle{ 0\lt x_i\lt \beta\lt x_j }[/math]. Replacing [math]\displaystyle{ x_i }[/math] by [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ x_j }[/math] by [math]\displaystyle{ \frac{x_ix_j}{\beta} }[/math]leaves the geometric mean unchanged but strictly decreases the arithmetic mean since

[math]\displaystyle{ x_i + x_j - \beta - \frac{x_i x_j}\beta = \frac{(\beta - x_i)(x_j - \beta)}\beta \gt 0 }[/math]. The proof then follows along similar lines as in the earlier replacement.

Induction proofs

Proof by induction #1

Of the non-negative real numbers x₁, . . . , x_n, the AM–GM statement is equivalent to

[math]\displaystyle{ \alpha^n\ge x_1 x_2 \cdots x_n }[/math]

with equality if and only if α = x_i for all i ∈ {1, . . . , n}.

For the following proof we apply mathematical induction and only well-known rules of arithmetic.

Induction basis: For n = 1 the statement is true with equality.

Induction hypothesis: Suppose that the AM–GM statement holds for all choices of n non-negative real numbers.

Induction step: Consider n + 1 non-negative real numbers x₁, . . . , x_n+1, . Their arithmetic mean α satisfies

[math]\displaystyle{ (n+1)\alpha=\ x_1 + \cdots + x_n + x_{n+1}. }[/math]

If all the x_i are equal to α, then we have equality in the AM–GM statement and we are done. In the case where some are not equal to α, there must exist one number that is greater than the arithmetic mean α, and one that is smaller than α. Without loss of generality, we can reorder our x_i in order to place these two particular elements at the end: x_n > α and x_n+1 < α. Then

[math]\displaystyle{ x_n - \alpha \gt 0\qquad \alpha-x_{n+1}\gt 0 }[/math]

[math]\displaystyle{ \implies (x_n-\alpha)(\alpha-x_{n+1})\gt 0\,.\qquad(*) }[/math]

Now define y with

[math]\displaystyle{ y:=x_n+x_{n+1}-\alpha\ge x_n-\alpha\gt 0\,, }[/math]

and consider the n numbers x₁, . . . , x_n–1, y which are all non-negative. Since

[math]\displaystyle{ (n+1)\alpha=x_1 + \cdots + x_{n-1} + x_n + x_{n+1} }[/math]

[math]\displaystyle{ n\alpha=x_1 + \cdots + x_{n-1} + \underbrace{x_n+x_{n+1}-\alpha}_{=\,y}, }[/math]

Thus, α is also the arithmetic mean of n numbers x₁, . . . , x_n–1, y and the induction hypothesis implies

[math]\displaystyle{ \alpha^{n+1}=\alpha^n\cdot\alpha\ge x_1x_2 \cdots x_{n-1} y\cdot\alpha.\qquad(**) }[/math]

Due to (*) we know that

[math]\displaystyle{ (\underbrace{x_n+x_{n+1}-\alpha}_{=\,y})\alpha-x_nx_{n+1}=(x_n-\alpha)(\alpha-x_{n+1})\gt 0, }[/math]

hence

[math]\displaystyle{ y\alpha\gt x_nx_{n+1}\,,\qquad({*}{*}{*}) }[/math]

in particular α > 0. Therefore, if at least one of the numbers x₁, . . . , x_n–1 is zero, then we already have strict inequality in (**). Otherwise the right-hand side of (**) is positive and strict inequality is obtained by using the estimate (***) to get a lower bound of the right-hand side of (**). Thus, in both cases we can substitute (***) into (**) to get

[math]\displaystyle{ \alpha^{n+1}\gt x_1x_2 \cdots x_{n-1} x_nx_{n+1}\,, }[/math]

which completes the proof.

Proof by induction #2

First of all we shall prove that for real numbers x₁ < 1 and x₂ > 1 there follows

[math]\displaystyle{ x_1 + x_2 \gt x_1x_2+1. }[/math]

Indeed, multiplying both sides of the inequality x₂ > 1 by 1 – x₁, gives

[math]\displaystyle{ x_2 - x_1x_2 \gt 1 - x_1, }[/math]

whence the required inequality is obtained immediately.

Now, we are going to prove that for positive real numbers x₁, . . . , x_n satisfying x₁ . . . x_n = 1, there holds

[math]\displaystyle{ x_1 + \cdots + x_n \ge n. }[/math]

The equality holds only if x₁ = ... = x_n = 1.

Induction basis: For n = 2 the statement is true because of the above property.

Induction hypothesis: Suppose that the statement is true for all natural numbers up to n – 1.

Induction step: Consider natural number n, i.e. for positive real numbers x₁, . . . , x_n, there holds x₁ . . . x_n = 1. There exists at least one x_k < 1, so there must be at least one x_j > 1. Without loss of generality, we let k =n – 1 and j = n.

Further, the equality x₁ . . . x_n = 1 we shall write in the form of (x₁ . . . x_n–2) (x_n–1 x_n) = 1. Then, the induction hypothesis implies

[math]\displaystyle{ (x_1 + \cdots + x_{n-2}) + (x_{n-1} x_n ) \gt n - 1. }[/math]

However, taking into account the induction basis, we have

[math]\displaystyle{ \begin{align} x_1 + \cdots + x_{n-2} + x_{n-1} + x_n & = (x_1 + \cdots + x_{n-2}) + (x_{n-1} + x_n ) \\ &\gt (x_1 + \cdots + x_{n-2}) + x_{n-1} x_n + 1 \\ & \gt n, \end{align} }[/math]

which completes the proof.

For positive real numbers a₁, . . . , a_n, let's denote

[math]\displaystyle{ x_1 = \frac{a_1}{\sqrt[n]{a_1\cdots a_n}}, . . ., x_n = \frac{a_n}{\sqrt[n]{a_1\cdots a_n}}. }[/math]

The numbers x₁, . . . , x_n satisfy the condition x₁ . . . x_n = 1. So we have

[math]\displaystyle{ \frac{a_1}{\sqrt[n]{a_1\cdots a_n}} + \cdots + \frac{a_n}{\sqrt[n]{a_1\cdots a_n}} \ge n, }[/math]

whence we obtain

[math]\displaystyle{ \frac{a_1 + \cdots + a_n}n \ge \sqrt[n]{a_1\cdots a_n}, }[/math]

with the equality holding only for a₁ = ... = a_n.

Proof by Cauchy using forward–backward induction

The following proof by cases relies directly on well-known rules of arithmetic but employs the rarely used technique of forward-backward-induction. It is essentially from Augustin Louis Cauchy and can be found in his Cours d'analyse.

The case where all the terms are equal

If all the terms are equal:

[math]\displaystyle{ x_1 = x_2 = \cdots = x_n, }[/math]

then their sum is nx₁, so their arithmetic mean is x₁; and their product is x₁ⁿ, so their geometric mean is x₁; therefore, the arithmetic mean and geometric mean are equal, as desired.

The case where not all the terms are equal

It remains to show that if not all the terms are equal, then the arithmetic mean is greater than the geometric mean. Clearly, this is only possible when n > 1.

This case is significantly more complex, and we divide it into subcases.

The subcase where n = 2

If n = 2, then we have two terms, x₁ and x₂, and since (by our assumption) not all terms are equal, we have:

[math]\displaystyle{ \begin{align} \Bigl(\frac{x_1+x_2}{2}\Bigr)^2-x_1x_2 &=\frac14(x_1^2+2x_1x_2+x_2^2)-x_1x_2\\ &=\frac14(x_1^2-2x_1x_2+x_2^2)\\ &=\Bigl(\frac{x_1-x_2}{2}\Bigr)^2\gt 0, \end{align} }[/math]

hence

[math]\displaystyle{ \frac{x_1 + x_2}{2} \ge \sqrt{x_1 x_2} }[/math]

as desired.

The subcase where n = 2^k

Consider the case where n = 2^k, where k is a positive integer. We proceed by mathematical induction.

In the base case, k = 1, so n = 2. We have already shown that the inequality holds when n = 2, so we are done.

Now, suppose that for a given k > 1, we have already shown that the inequality holds for n = 2^k−1, and we wish to show that it holds for n = 2^k. To do so, we apply the inequality twice for 2^k-1 numbers and once for 2 numbers to obtain:

[math]\displaystyle{ \begin{align} \frac{x_1 + x_2 + \cdots + x_{2^k}}{2^k} & {} =\frac{\frac{x_1 + x_2 + \cdots + x_{2^{k-1}}}{2^{k-1}} + \frac{x_{2^{k-1} + 1} + x_{2^{k-1} + 2} + \cdots + x_{2^k}}{2^{k-1}}}{2} \\[7pt] & \ge \frac{\sqrt[2^{k-1}]{x_1 x_2 \cdots x_{2^{k-1}}} + \sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} \cdots x_{2^k}}}{2} \\[7pt] & \ge \sqrt{\sqrt[2^{k-1}]{x_1 x_2 \cdots x_{2^{k-1}}} \sqrt[2^{k-1}]{x_{2^{k-1} + 1} x_{2^{k-1} + 2} \cdots x_{2^k}}} \\[7pt] & = \sqrt[2^k]{x_1 x_2 \cdots x_{2^k}} \end{align} }[/math]

where in the first inequality, the two sides are equal only if

[math]\displaystyle{ x_1 = x_2 = \cdots = x_{2^{k-1}} }[/math]

and

[math]\displaystyle{ x_{2^{k-1}+1} = x_{2^{k-1}+2} = \cdots = x_{2^k} }[/math]

(in which case the first arithmetic mean and first geometric mean are both equal to x₁, and similarly with the second arithmetic mean and second geometric mean); and in the second inequality, the two sides are only equal if the two geometric means are equal. Since not all 2^k numbers are equal, it is not possible for both inequalities to be equalities, so we know that:

[math]\displaystyle{ \frac{x_1 + x_2 + \cdots + x_{2^k}}{2^k} \ge \sqrt[2^k]{x_1 x_2 \cdots x_{2^k}} }[/math]

as desired.

The subcase where n < 2^k

If n is not a natural power of 2, then it is certainly less than some natural power of 2, since the sequence 2, 4, 8, . . . , 2^k, . . . is unbounded above. Therefore, without loss of generality, let m be some natural power of 2 that is greater than n.

So, if we have n terms, then let us denote their arithmetic mean by α, and expand our list of terms thus:

[math]\displaystyle{ x_{n+1} = x_{n+2} = \cdots = x_m = \alpha. }[/math]

We then have:

[math]\displaystyle{ \begin{align} \alpha & = \frac{x_1 + x_2 + \cdots + x_n}{n} \\[6pt] & = \frac{\frac{m}{n} \left( x_1 + x_2 + \cdots + x_n \right)}{m} \\[6pt] & = \frac{x_1 + x_2 + \cdots + x_n + \frac{(m-n)}{n} \left( x_1 + x_2 + \cdots + x_n \right)}{m} \\[6pt] & = \frac{x_1 + x_2 + \cdots + x_n + \left( m-n \right) \alpha}{m} \\[6pt] & = \frac{x_1 + x_2 + \cdots + x_n + x_{n+1} + \cdots + x_m}{m} \\[6pt] & \ge \sqrt[m]{x_1 x_2 \cdots x_n x_{n+1} \cdots x_m} \\[6pt] & = \sqrt[m]{x_1 x_2 \cdots x_n \alpha^{m-n}}\,, \end{align} }[/math]

so

[math]\displaystyle{ \alpha^m \ge x_1 x_2 \cdots x_n \alpha^{m-n} }[/math]

and

[math]\displaystyle{ \alpha \ge \sqrt[n]{x_1 x_2 \cdots x_n} }[/math]

as desired.

Proof by induction using basic calculus

The following proof uses mathematical induction and some basic differential calculus.

Induction basis: For n = 1 the statement is true with equality.

Induction hypothesis: Suppose that the AM–GM statement holds for all choices of n non-negative real numbers.

Induction step: In order to prove the statement for n + 1 non-negative real numbers x₁, . . . , x_n, x_n+1, we need to prove that

[math]\displaystyle{ \frac{x_1 + \cdots + x_n + x_{n+1}}{n+1} - ({x_1 \cdots x_n x_{n+1}})^{\frac{1}{n+1}}\ge0 }[/math]

with equality only if all the n + 1 numbers are equal.

If all numbers are zero, the inequality holds with equality. If some but not all numbers are zero, we have strict inequality. Therefore, we may assume in the following, that all n + 1 numbers are positive.

We consider the last number x_n+1 as a variable and define the function

[math]\displaystyle{ f(t)=\frac{x_1 + \cdots + x_n + t}{n+1} - ({x_1 \cdots x_n t})^{\frac{1}{n+1}},\qquad t\gt 0. }[/math]

Proving the induction step is equivalent to showing that f(t) ≥ 0 for all t > 0, with f(t) = 0 only if x₁, . . . , x_n and t are all equal. This can be done by analyzing the critical points of f using some basic calculus.

The first derivative of f is given by

[math]\displaystyle{ f'(t)=\frac{1}{n+1}-\frac{1}{n+1}({x_1 \cdots x_n})^{\frac{1}{n+1}}t^{-\frac{n}{n+1}},\qquad t\gt 0. }[/math]

A critical point t₀ has to satisfy f′(t₀) = 0, which means

[math]\displaystyle{ ({x_1 \cdots x_n})^{\frac{1}{n+1}}t_0^{-\frac{n}{n+1}}=1. }[/math]

After a small rearrangement we get

[math]\displaystyle{ t_0^{\frac{n}{n+1}}=({x_1 \cdots x_n})^{\frac{1}{n+1}}, }[/math]

and finally

[math]\displaystyle{ t_0=({x_1 \cdots x_n})^{\frac{1}n}, }[/math]

which is the geometric mean of x₁, . . . , x_n. This is the only critical point of f. Since f′′(t) > 0 for all t > 0, the function f is strictly convex and has a strict global minimum at t₀. Next we compute the value of the function at this global minimum:

[math]\displaystyle{ \begin{align} f(t_0) &= \frac{x_1 + \cdots + x_n + ({x_1 \cdots x_n})^{1/n}}{n+1} - ({x_1 \cdots x_n})^{\frac{1}{n+1}}({x_1 \cdots x_n})^{\frac{1}{n(n+1)}}\\ &= \frac{x_1 + \cdots + x_n}{n+1} + \frac{1}{n+1}({x_1 \cdots x_n})^{\frac{1}n} - ({x_1 \cdots x_n})^{\frac{1}n}\\ &= \frac{x_1 + \cdots + x_n}{n+1} - \frac{n}{n+1}({x_1 \cdots x_n})^{\frac{1}n}\\ &= \frac{n}{n+1}\Bigl(\frac{x_1 + \cdots + x_n}n - ({x_1 \cdots x_n})^{\frac{1}n}\Bigr) \\ &\ge0, \end{align} }[/math]

where the final inequality holds due to the induction hypothesis. The hypothesis also says that we can have equality only when x₁, . . . , x_n are all equal. In this case, their geometric mean  t₀ has the same value, Hence, unless x₁, . . . , x_n, x_n+1 are all equal, we have f(x_n+1) > 0. This completes the proof.

This technique can be used in the same manner to prove the generalized AM–GM inequality and Cauchy–Schwarz inequality in Euclidean space Rⁿ.

Proof by Pólya using the exponential function

George Pólya provided a proof similar to what follows. Let f(x) = e^x–1 – x for all real x, with first derivative f′(x) = e^x–1 – 1 and second derivative f′′(x) = e^x–1. Observe that f(1) = 0, f′(1) = 0 and f′′(x) > 0 for all real x, hence f is strictly convex with the absolute minimum at x = 1. Hence x ≤ e^x–1 for all real x with equality only for x = 1.

Consider a list of non-negative real numbers x₁, x₂, . . . , x_n. If they are all zero, then the AM–GM inequality holds with equality. Hence we may assume in the following for their arithmetic mean α > 0. By n-fold application of the above inequality, we obtain that

[math]\displaystyle{ \begin{align}{ \frac{x_1}{\alpha} \frac{x_2}{\alpha} \cdots \frac{x_n}{\alpha} } &\le { e^{\frac{x_1}{\alpha} - 1} e^{\frac{x_2}{\alpha} - 1} \cdots e^{\frac{x_n}{\alpha} - 1} }\\ & = \exp \Bigl( \frac{x_1}{\alpha} - 1 + \frac{x_2}{\alpha} - 1 + \cdots + \frac{x_n}{\alpha} - 1 \Bigr), \qquad (*) \end{align} }[/math]

with equality if and only if x_i = α for every i ∈ {1, . . . , n}. The argument of the exponential function can be simplified:

[math]\displaystyle{ \begin{align} \frac{x_1}{\alpha} - 1 + \frac{x_2}{\alpha} - 1 + \cdots + \frac{x_n}{\alpha} - 1 & = \frac{x_1 + x_2 + \cdots + x_n}{\alpha} - n \\ & = \frac{n \alpha}{\alpha} - n \\ & = 0. \end{align} }[/math]

Returning to (*),

[math]\displaystyle{ \frac{x_1 x_2 \cdots x_n}{\alpha^n} \le e^0 = 1, }[/math]

which produces x₁ x₂ · · · x_n ≤ αⁿ, hence the result

[math]\displaystyle{ \sqrt[n]{x_1 x_2 \cdots x_n} \le \alpha. }[/math]

Proof by Lagrangian multipliers

If any of the [math]\displaystyle{ x_i }[/math] are [math]\displaystyle{ 0 }[/math], then there is nothing to prove. So we may assume all the [math]\displaystyle{ x_i }[/math] are strictly positive.

Because the arithmetic and geometric means are homogeneous of degree 1, without loss of generality assume that [math]\displaystyle{ \prod_{i=1}^n x_i = 1 }[/math]. Set [math]\displaystyle{ G(x_1,x_2,\ldots,x_n)=\prod_{i=1}^n x_i }[/math], and [math]\displaystyle{ F(x_1,x_2,\ldots,x_n) = \frac{1}{n}\sum_{i=1}^n x_i }[/math]. The inequality will be proved (together with the equality case) if we can show that the minimum of [math]\displaystyle{ F(x_1,x_2,...,x_n), }[/math] subject to the constraint [math]\displaystyle{ G(x_1,x_2,\ldots,x_n) = 1, }[/math] is equal to [math]\displaystyle{ 1 }[/math], and the minimum is only achieved when [math]\displaystyle{ x_1 = x_2 = \cdots = x_n = 1 }[/math]. Let us first show that the constrained minimization problem has a global minimum.

Set [math]\displaystyle{ K = \{(x_1,x_2,\ldots,x_n) \colon 0 \leq x_1,x_2,\ldots,x_n \leq n\} }[/math]. Since the intersection [math]\displaystyle{ K \cap \{G = 1\} }[/math] is compact, the extreme value theorem guarantees that the minimum of [math]\displaystyle{ F(x_1,x_2,...,x_n) }[/math] subject to the constraints [math]\displaystyle{ G(x_1,x_2,\ldots,x_n) = 1 }[/math] and [math]\displaystyle{ (x_1,x_2,\ldots,x_n) \in K }[/math] is attained at some point inside [math]\displaystyle{ K }[/math]. On the other hand, observe that if any of the [math]\displaystyle{ x_i \gt n }[/math], then [math]\displaystyle{ F(x_1,x_2,\ldots,x_n) \gt 1 }[/math], while [math]\displaystyle{ F(1,1,\ldots,1) = 1 }[/math], and [math]\displaystyle{ (1,1,\ldots,1) \in K \cap \{G = 1\} }[/math]. This means that the minimum inside [math]\displaystyle{ K \cap \{G = 1\} }[/math] is in fact a global minimum, since the value of [math]\displaystyle{ F }[/math] at any point inside [math]\displaystyle{ K \cap \{G = 1\} }[/math] is certainly no smaller than the minimum, and the value of [math]\displaystyle{ F }[/math] at any point [math]\displaystyle{ (y_1,y_2,\ldots, y_n) }[/math] not inside [math]\displaystyle{ K }[/math] is strictly bigger than the value at [math]\displaystyle{ (1,1,\ldots,1) }[/math], which is no smaller than the minimum.

The method of Lagrange multipliers says that the global minimum is attained at a point [math]\displaystyle{ (x_1,x_2,\ldots,x_n) }[/math] where the gradient of [math]\displaystyle{ F(x_1,x_2,\ldots,x_n) }[/math] is [math]\displaystyle{ \lambda }[/math] times the gradient of [math]\displaystyle{ G(x_1,x_2,\ldots,x_n) }[/math], for some [math]\displaystyle{ \lambda }[/math]. We will show that the only point at which this happens is when [math]\displaystyle{ x_1 = x_2 = \cdots = x_n = 1 }[/math] and [math]\displaystyle{ F(x_1,x_2,...,x_n) = 1. }[/math]

Compute [math]\displaystyle{ \frac{\partial F}{\partial x_i} = \frac{1}{n} }[/math] and

[math]\displaystyle{ \frac{\partial G}{\partial x_i} = \prod_{j \neq i}x_j = \frac{G(x_1,x_2,\ldots,x_n)}{x_i} = \frac{1}{x_i} }[/math]

along the constraint. Setting the gradients proportional to one another therefore gives for each [math]\displaystyle{ i }[/math] that [math]\displaystyle{ \frac{1}{n} = \frac{\lambda}{x_i}, }[/math] and so [math]\displaystyle{ n\lambda= x_i. }[/math] Since the left-hand side does not depend on [math]\displaystyle{ i }[/math], it follows that [math]\displaystyle{ x_1 = x_2 = \cdots = x_n }[/math], and since [math]\displaystyle{ G(x_1,x_2,\ldots, x_n) = 1 }[/math], it follows that [math]\displaystyle{ x_1 = x_2 = \cdots = x_n = 1 }[/math] and [math]\displaystyle{ F(x_1,x_2,\ldots,x_n) = 1 }[/math], as desired.

Generalizations

Weighted AM–GM inequality

There is a similar inequality for the weighted arithmetic mean and weighted geometric mean. Specifically, let the nonnegative numbers x₁, x₂, . . . , x_n and the nonnegative weights w₁, w₂, . . . , w_n be given. Set w = w₁ + w₂ + · · · + w_n. If w > 0, then the inequality

[math]\displaystyle{ \frac{w_1 x_1 + w_2 x_2 + \cdots + w_n x_n}{w} \ge \sqrt[w]{x_1^{w_1} x_2^{w_2} \cdots x_n^{w_n}} }[/math]

holds with equality if and only if all the x_k with w_k > 0 are equal. Here the convention 0⁰ = 1 is used.

If all w_k = 1, this reduces to the above inequality of arithmetic and geometric means.

One stronger version of this, which also gives strengthened version of the unweighted version, is due to Aldaz. In particular, There is a similar inequality for the weighted arithmetic mean and weighted geometric mean. Specifically, let the nonnegative numbers x₁, x₂, . . . , x_n and the nonnegative weights w₁, w₂, . . . , w_n be given. Assume further that the sum of the weights is 1. Then [math]\displaystyle{ \sum_{i=1}^n w_ix_i \geq \prod_{i=1}^n x_i^{w_i} + \sum_{i=1}^n w_i\left(x_i^{\frac{1}{2}} -\sum_{i=1}^n w_ix_i^{\frac{1}{2}} \right)^2 }[/math].

Proof using Jensen's inequality

Using the finite form of Jensen's inequality for the natural logarithm, we can prove the inequality between the weighted arithmetic mean and the weighted geometric mean stated above.

Since an x_k with weight w_k = 0 has no influence on the inequality, we may assume in the following that all weights are positive. If all x_k are equal, then equality holds. Therefore, it remains to prove strict inequality if they are not all equal, which we will assume in the following, too. If at least one x_k is zero (but not all), then the weighted geometric mean is zero, while the weighted arithmetic mean is positive, hence strict inequality holds. Therefore, we may assume also that all x_k are positive.

Since the natural logarithm is strictly concave, the finite form of Jensen's inequality and the functional equations of the natural logarithm imply

[math]\displaystyle{ \begin{align} \ln\Bigl(\frac{w_1x_1+\cdots+w_nx_n}w\Bigr) & \gt \frac{w_1}w\ln x_1+\cdots+\frac{w_n}w\ln x_n \\ & =\ln \sqrt[w]{x_1^{w_1} x_2^{w_2} \cdots x_n^{w_n}}. \end{align} }[/math]

Since the natural logarithm is strictly increasing,

[math]\displaystyle{ \frac{w_1x_1+\cdots+w_nx_n}w \gt \sqrt[w]{x_1^{w_1} x_2^{w_2} \cdots x_n^{w_n}}. }[/math]

Matrix arithmetic–geometric mean inequality

Most matrix generalizations of the arithmetic geometric mean inequality apply on the level of unitarily invariant norms, owing to the fact that even if the matrices [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] are positive semi-definite the matrix [math]\displaystyle{ A B }[/math] may not be positive semi-definite and hence may not have a canonical square root. In Bhatia and Kittaneh proved that for any unitarily invariant norm [math]\displaystyle{ |||\cdot||| }[/math] and positive semi-definite matrices [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] it is the case that

[math]\displaystyle{ |||AB|||\leq \frac{1}{2}|||A^2 + B^2||| }[/math]

Later, in the same authors proved the stronger inequality that

[math]\displaystyle{ |||AB||| \leq \frac{1}{4}|||(A+B)^2||| }[/math]

Finally, it is known for dimension [math]\displaystyle{ n=2 }[/math] that the following strongest possible matrix generalization of the arithmetic-geometric mean inequality holds, and it is conjectured to hold for all [math]\displaystyle{ n }[/math]

[math]\displaystyle{ |||(AB)^{\frac{1}{2}}|||\leq \frac{1}{2}|||A+B||| }[/math]

This conjectured inequality was shown by Stephen Drury in 2012. Indeed, he proved

[math]\displaystyle{ \sqrt{\sigma_j(AB)}\leq \frac{1}{2}\lambda_j(A+B), \ j=1, \ldots, n. }[/math]

Other generalizations

Other generalizations of the inequality of arithmetic and geometric means include:

• Muirhead's inequality,
• Maclaurin's inequality,
• Generalized mean inequality,
• Means of complex numbers.

See also

• Hoffman's packing puzzle
• Ky Fan inequality
• Young's inequality for products

External links

• Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format. http://www.mediafire.com/file/1mw1tkgozzu.