Evolving networks
Evolving Networks are networks that change as a function of time. They are a natural extension of network science since almost all real world networks evolve over time, either by adding or removing nodes or links over time. Often all of these processes occur simultaneously, such as in social networks where people make and lose friends over time, thereby creating and destroying edges, and some people become part of new social networks or leave their networks, changing the nodes in the network. Evolving network concepts build on established network theory and are now being introduced into studying networks in many diverse fields.
Network theory background
The study of networks traces its foundations to the development of graph theory, which was first analyzed by Leonhard Euler in 1736 when he wrote the famous Seven Bridges of Königsberg paper. Probabilistic network theory then developed with the help of eight famous papers studying random graphs written by Paul Erdős and Alfréd Rényi. The Erdős-Rényi model (ER) supposes that a graph is composed of N labeled nodes where each pair of nodes is connected by a preset probability p.
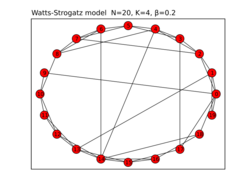
While the ER model's simplicity has helped it find many applications, it does not accurately describe many real world networks. The ER model fails to generate local clustering and triadic closures as often as they are found in real world networks. Therefore, the Watts and Strogatz model was proposed, whereby a network is constructed as a regular ring lattice, and then nodes are rewired according to some probability β.[1] This produces a locally clustered network and dramatically reduces the average path length, creating networks which represent the small world phenomenon observed in many real world networks.[2]
Despite this achievement, both the ER and the Watts and Storgatz models fail to account for the formulation of hubs as observed in many real world networks. The degree distribution in the ER model follows a Poisson distribution, while the Watts and Strogatz model produces graphs that are homogeneous in degree. Many networks are instead scale free, meaning that their degree distribution follows a power law of the form:
- [math]\displaystyle{ P\left(k\right)\sim k^{-\gamma} }[/math]
This exponent turns out to be approximately 3 for many real world networks, however, it is not a universal constant and depends continuously on the network's parameters [3]
First evolving network model - scale free networks
The Barabási–Albert (BA) model was the first widely accepted model to produce scale-free networks. This was accomplished by incorporating preferential attachment and growth, where nodes are added to the network over time and are more likely to link to other nodes with high degree distributions. The BA model was first applied to degree distributions on the web, where both of these effects can be clearly seen. New web pages are added over time, and each new page is more likely to link to highly visible hubs like Google which have high degree distributions than to nodes with only a few links. Formally this preferential attachment is:
- [math]\displaystyle{ p_i = \frac{k_i}{\displaystyle\sum_j k_j}, }[/math]
Additions to BA model
The BA model was the first model to derive the network topology from the way the network was constructed with nodes and links being added over time. However, the model makes only the simplest assumptions necessary for a scale-free network to emerge, namely that there is linear growth and linear preferential attachment. This minimal model does not capture variations in the shape of the degree distribution, variations in the degree exponent, or the size independent clustering coefficient. Therefore, the original model has since been modified[by whom?] to more fully capture the properties of evolving networks by introducing a few new properties.
Fitness
One concern with the BA model is that the degree distributions of each nodes experience strong positive feedback whereby the earliest nodes with high degree distributions continue to dominate the network indefinitely. However, this can be alleviated by introducing a fitness for each node, which modifies the probability of new links being created with that node or even of links to that node being removed.[4]
In order to preserve the preferential attachment from the BA model, this fitness is then multiplied by the preferential attachment based on degree distribution to give the true probability that a link is created which connects to node i.
- [math]\displaystyle{ \Pi(k_i) = \frac{\eta_i k_i}{\displaystyle\sum_j \eta_j k_j}, }[/math]
Where [math]\displaystyle{ \eta }[/math] is the fitness, which may also depend on time. A decay of fitness with respect to time may occur and can be formalized by:
[math]\displaystyle{ \Pi(k_i) \propto k_i(t-t_i)^{-\nu}, }[/math]
Where [math]\displaystyle{ \gamma }[/math] increases with [math]\displaystyle{ \nu }[/math]
Removing nodes and rewiring links
Further complications arise because nodes may be removed from the network with some probability. Additionally, existing links may be destroyed and new links between existing nodes may be created. The probability of these actions occurring may depend on time and may also be related to the node's fitness. Probabilities can be assigned to these events by studying the characteristics of the network in question in order to grow a model network with identical properties. This growth would take place with one of the following actions occurring at each time step:
Prob p: add an internal link.
Prob q: delete a link.
Prob r: delete a node.
Prob 1-p-q-r: add a node.
Other ways of characterizing evolving networks
In addition to growing network models as described above, there may be times when other methods are more useful or convenient for characterizing certain properties of evolving networks.
Convergence towards Equilibria
In networked systems where competitive decision making takes place, game theory is often used to model system dynamics, and convergence towards equilibria can be considered as a driver of topological evolution. For example, Kasthurirathna and Piraveenan [5] have shown that when individuals in a system display varying levels of rationality, improving the overall system rationality might be an evolutionary reason for the emergence of scale-free networks. They demonstrated this by applying evolutionary pressure on an initially random network which simulates a range of classic games, so that the network converges towards Nash equilibria while being allowed to re-wire. The networks become increasingly scale-free during this process.
Treat evolving networks as successive snapshots of a static network
The most common way to view evolving networks is by considering them as successive static networks. This could be conceptualized as the individual still images which compose a motion picture. Many simple parameters exist to describe a static network (number of nodes, edges, path length, connected components), or to describe specific nodes in the graph such as the number of links or the clustering coefficient. These properties can then individually be studied as a time series using signal processing notions.Cite error: Closing </ref> missing for <ref> tag Other similar properties can be defined and then it is possible to instead track these properties through the evolution of a network and visualize them directly.
Another issue with using successive snapshots is that only slight changes in network topology can have large effects on the outcome of algorithms designed to find communities. Therefore, it is necessary to use a non classical definition of communities which permits following the evolution of the community through a set of rules such as birth, death, merge, split, growth, and contraction.[6][7]
Applications
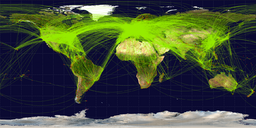
Almost all real world networks are evolving networks since they are constructed over time. By varying the respective probabilities described above, it is possible to use the expanded BA model to construct a network with nearly identical properties as many observed networks.[8] Moreover, the concept of scale free networks shows us that time evolution is a necessary part of understanding the network's properties, and that it is difficult to model an existing network as having been created instantaneously. Real evolving networks which are currently being studied include social networks, communications networks, the internet, the movie actor network, the world wide web, and transportation networks.
Further reading
- "Understanding Network Science," https://web.archive.org/web/20110718151116/http://www.zangani.com/blog/2007-1030-networkingscience
- "Linked: The New Science of Networks", A.-L. Barabási Perseus Publishing, Cambridge.
References
- ↑ Watts, D.J.; Strogatz, S.H. (1998). "Collective dynamics of 'small-world' networks". Nature 393 (6684): 409–10. doi:10.1038/30918. PMID 9623998. Bibcode: 1998Natur.393..440W. http://www.nature.com/nature/journal/v393/n6684/abs/393440a0.html. Retrieved 2014-01-31.
- ↑ Travers Jeffrey; Milgram Stanley (1969). "An Experimental Study of the Small World Problem". Sociometry 32 (4): 425–443. doi:10.2307/2786545.
- ↑ R. Albert; A.-L. Barabási (2000). "Topology of Evolving Networks: Local Events and Universality". Physical Review Letters 85: 5234–5237. doi:10.1103/PhysRevLett.85.5234. PMID 11102229. Bibcode: 2000PhRvL..85.5234A. http://nd.edu/~networks/Publication%20Categories/03%20Journal%20Articles/Physics/Universality_Physical%20Rev%20Ltrs%2085,%205234%20(2000).pdf.
- ↑ Albert R. and Barabási A.-L., "Statistical mechanics of complex networks", Reviews of Modern Physics 74, 47 (2002)
- ↑ Kasthurirathna, Dharshana; Piraveenan, Mahendra. (2015). "Emergence of scale-free characteristics in socioecological systems with bounded rationality". Scientific Reports In Press.
- ↑ Y. Chi, S. Zhu; X. Song; J. Tatemura; B.L. Tseng (2007). "Structural and temporal analysis of the blogosphere through community factorization". KDD ’07: Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining: 163–172. http://portal.acm.org/ft_gateway.cfm?id=1281213&type=pdf.
- ↑ I. Farkas et al. (2002). "Networks in life: scaling properties and eigenvalue spectra". Physica 314: 25–34. doi:10.1016/S0378-4371(02)01181-0. Bibcode: 2002PhyA..314...25F. http://www.barabasilab.com/pubs/CCNR-ALB_Publications/200211-01_PhysA-NetworksInLife/200211-01_PhysA-NetworksInLife.pdf.
 |
