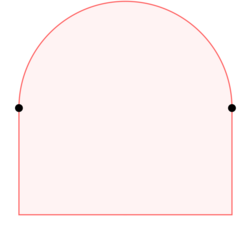
Exposed point

The two distinguished points are examples of extreme points of a convex set that are not exposed

In mathematics, an exposed point of a convex set [math]\displaystyle{ C }[/math] is a point [math]\displaystyle{ x\in C }[/math] at which some continuous linear functional attains its strict maximum over [math]\displaystyle{ C }[/math]. Such a functional is then said to expose [math]\displaystyle{ x }[/math]. There can be many exposing functionals for [math]\displaystyle{ x }[/math]. The set of exposed points of [math]\displaystyle{ C }[/math] is usually denoted [math]\displaystyle{ \exp(C) }[/math].

A stronger notion is that of strongly exposed point of [math]\displaystyle{ C }[/math] which is an exposed point [math]\displaystyle{ x \in C }[/math] such that some exposing functional [math]\displaystyle{ f }[/math] of [math]\displaystyle{ x }[/math] attains its strong maximum over [math]\displaystyle{ C }[/math] at [math]\displaystyle{ x }[/math], i.e. for each sequence [math]\displaystyle{ (x_n) \subset C }[/math] we have the following implication: [math]\displaystyle{ f(x_n) \to \max f(C) \Longrightarrow \|x_n -x\| \to 0 }[/math]. The set of all strongly exposed points of [math]\displaystyle{ C }[/math] is usually denoted [math]\displaystyle{ \operatorname{str}\exp(C) }[/math].

There are two weaker notions, that of extreme point and that of support point of [math]\displaystyle{ C }[/math].