Extreme set

The two distinguished points are examples of extreme points of a convex set that are not exposed points. Therefore, not every convex face of a convex set is an exposed face.

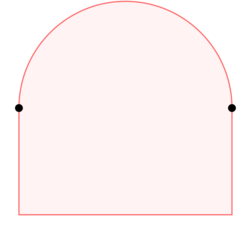
In mathematics, most commonly in convex geometry, an extreme set or face of a set $C\subseteq V$ in a vector space $V$ is a subset $F\subseteq C$ with the property that if for any two points $x,y\in C$ some in-between point $z=\theta x+(1-\theta )y,\theta \in [0,1]$ lies in $F$, then we must have had $x,y\in F$.

An extreme point of $C$ is a point $p\in C$ for which $\{p\}$ is a face.

An exposed face of $C$ is the subset of points of $C$ where a linear functional achieves its minimum on $C$. Thus, if $f$ is a linear functional on $V$ and $\alpha =\inf \{f(c):c\in C\}>-\mathrm{\infty }$, then $\{c\in C:f(c)=\alpha \}$ is an exposed face of $C$.

An exposed point of $C$ is a point $p\in C$ such that $\{p\}$ is an exposed face. That is, $f(p)>f(c)$ for all $c\in C\setminus \{p\}$.

An exposed face is a face, but the converse is not true (see the figure). An exposed face of $C$ is convex if $C$ is convex. If $F$ is a face of $C\subseteq V$, then $E\subseteq F$ is a face of $F$ if and only if $E$ is a face of $C$.

Competing definitions

Some authors do not include $C$ and/or $\varnothing$ among the (exposed) faces. Some authors require $F$ and/or $C$ to be convex (else the boundary of a disc is a face of the disc, as well as any subset of the boundary) or closed. Some authors require the functional $f$ to be continuous in a given vector topology.

See also

• Face (geometry)

Bibliography

• Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834. 

External links

• TOPOLOGICAL VECTOR SPACES AND CONTINUOUS LINEAR FUNCTIONALS, Chapter III of FUNCTIONAL ANALYSIS, Lawrence Baggett, University of Colorado Boulder.
• Functional Analysis, Peter Philip, Ludwig-Maximilians-universität München, 2024