Fabius function

Short description: Nowhere analytic, infinitely differentiable function

Graph of the Fabius function on the interval [0,1].

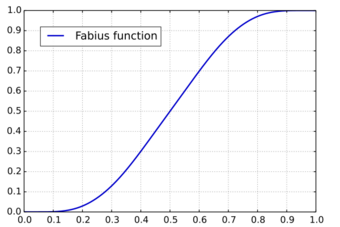
In mathematics, the Fabius function is an example of an infinitely differentiable function that is nowhere analytic, found by Jaap Fabius (1966).

This function satisfies the initial condition $f(0)=0$, the symmetry condition $f(1-x)=1-f(x)$ for $0\le x\le 1,$ and the functional differential equation

$f^{\prime }(x)=2f(2x)$

for $0\le x\le 1/2.$ It follows that $f(x)$ is monotone increasing for $0\le x\le 1,$ with $f(1/2)=1/2$ and $f(1)=1$ and $f^{\prime }(1-x)=f^{\prime }(x)$ and $f^{\prime }(x)+f^{\prime }(\frac{1}{2}-x)=2.$

It was also written down as the Fourier transform of

$\hat{f}(z)=\prod _{m=1}^{\mathrm{\infty }}{(\cos \frac{\pi z}{2^m})}^m$

by Børge Jessen and Aurel Wintner (1935).

The Fabius function is defined on the unit interval, and is given by the cumulative distribution function of

$\sum _{n=1}^{\mathrm{\infty }}{2}^{-n}{\xi }_n,$

where the ξ_n are independent uniformly distributed random variables on the unit interval. That distribution has an expectation of $\frac{1}{2}$ and a variance of $\frac{1}{36}$.

Extension of the function to the nonnegative real numbers.

There is a unique extension of f to the real numbers that satisfies the same differential equation for all x. This extension can be defined by f (x) = 0 for x ≤ 0, f (x + 1) = 1 − f (x) for 0 ≤ x ≤ 1, and f (x + 2^r) = −f (x) for 0 ≤ x ≤ 2^r with r a positive integer. The sequence of intervals within which this function is positive or negative follows the same pattern as the Thue–Morse sequence.

The Rvachëv up function is closely related: $$u(t)=\{\begin{array}{l}F(t+1),|t|<1\\ 0,|t|\ge 1\end{array}$$ which fulfills the Delay differential equation $$\frac{d}{dt}u(t)=2u(2t+1)-2u(2t-1).$$ (see Another example).

Values

The Fabius function is constant zero for all non-positive arguments, and assumes rational values at positive dyadic rational arguments. For example:

• $f(1)=1$
• $f(\frac{1}{2})=\frac{1}{2}$
• $f(\frac{1}{4})=\frac{5}{72}$
• $f(\frac{1}{8})=\frac{1}{288}$
• $f(\frac{1}{16})=\frac{143}{2073600}$
• $f(\frac{1}{32})=\frac{19}{33177600}$
• $f(\frac{1}{64})=\frac{1153}{561842749440}$
• $f(\frac{1}{128})=\frac{583}{179789679820800}$

with the numerators listed in OEIS: A272755 and denominators in OEIS: A272757.

Asymptotic

$\begin{array}{rl}\log f(x)& =-\frac{{\log }^{2}x}{2\log 2}+\frac{\log x\cdot \log (-\log x)}{\log 2}-(\frac{1}{2}+\frac{1+\log \log 2}{\log 2})\log x-\frac{{\log }^2(-\log x)}{2\log 2}+\frac{\log \log 2\cdot \log (-\log x)}{\log 2}\\ & +(\frac{6{\gamma }^2+12{\gamma }_1-{\pi }^2-6{\log }^2\log 2}{12\log 2}-\frac{7\log 2}{12}-\frac{\log \pi }{2})+\frac{{\log }^2(-\log x)}{2\log 2\cdot \log x}-\frac{\log \log 2\cdot \log (-\log x)}{\log 2\cdot \log x}+O\left(\frac{1}{\log x}\right)\end{array}$

for $x\to 0^{+},$ where $\gamma$ is Euler's constant, and ${\gamma }_1$ is the Stieltjes constant. Equivalently,

$\log f\left(2^{-n}\right)=-\frac{n^2\log 2}{2}-n\log n+(1+\frac{\log 2}{2})n-\frac{{\log }^{2}n}{2\log 2}+(\frac{6{\gamma }^2+12{\gamma }_1-{\pi }^2}{12\log 2}-\frac{7\log 2}{12}-\frac{\log \pi }{2})-\frac{{\log }^{2}n}{2n{\log }^{2}2}+O\left(\frac{1}{n}\right)$

for $n\to \mathrm{\infty }.$

References

• Fabius, J. (1966), "A probabilistic example of a nowhere analytic C ^∞-function", Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 5 (2): 173–174, doi:10.1007/bf00536652 
• Jessen, Børge; Wintner, Aurel (1935), "Distribution functions and the Riemann zeta function", Trans. Amer. Math. Soc. 38: 48–88, doi:10.1090/S0002-9947-1935-1501802-5 
• Dimitrov, Youri (2006). Polynomially-divided solutions of bipartite self-differential functional equations (Thesis).
• Arias de Reyna, Juan (2017). "Arithmetic of the Fabius function". arXiv:1702.06487 [math.NT].
• Arias de Reyna, Juan (2017). "An infinitely differentiable function with compact support: Definition and properties". arXiv:1702.05442 [math.CA]. (an English translation of the author's paper published in Spanish in 1982)
• Alkauskas, Giedrius (2001), "Dirichlet series associated with Thue-Morse sequence", preprint.
• Rvachev, V. L., Rvachev, V. A., "Non-classical methods of the approximation theory in boundary value problems", Naukova Dumka, Kiev (1979) (in Russian).