Fast multipole method

The fast multipole method (FMM) is a numerical technique that was developed to speed up the calculation of long-ranged forces in the n-body problem. It does this by expanding the system Green's function using a multipole expansion, which allows one to group sources that lie close together and treat them as if they are a single source.

The FMM has also been applied in accelerating the iterative solver in the method of moments (MOM) as applied to computational electromagnetics problems. The FMM was first introduced in this manner by Leslie Greengard and Vladimir Rokhlin Jr. and is based on the multipole expansion of the vector Helmholtz equation. By treating the interactions between far-away basis functions using the FMM, the corresponding matrix elements do not need to be explicitly stored, resulting in a significant reduction in required memory. If the FMM is then applied in a hierarchical manner, it can improve the complexity of matrix-vector products in an iterative solver from [math]\displaystyle{ \mathcal{O}(N^2) }[/math] to [math]\displaystyle{ \mathcal{O}(N) }[/math] in finite arithmetic, i.e., given a tolerance [math]\displaystyle{ \varepsilon }[/math], the matrix-vector product is guaranteed to be within a tolerance [math]\displaystyle{ \varepsilon. }[/math] The dependence of the complexity on the tolerance [math]\displaystyle{ \varepsilon }[/math] is [math]\displaystyle{ \mathcal{O}(\log(1/\varepsilon)) }[/math], i.e., the complexity of FMM is [math]\displaystyle{ \mathcal{O}(N\log(1/\varepsilon)) }[/math]. This has expanded the area of applicability of the MOM to far greater problems than were previously possible.

The FMM, introduced by Rokhlin Jr. and Greengard has been said to be one of the top ten algorithms of the 20th century. The FMM algorithm reduces the complexity of matrix-vector multiplication involving a certain type of dense matrix which can arise out of many physical systems.

The FMM has also been applied for efficiently treating the Coulomb interaction in the Hartree–Fock method and density functional theory calculations in quantum chemistry.

Sketch of the Algorithm

Fast Multipole Method - interpolation of a pole at x=3 with an order-5 Chebyshev polynomial

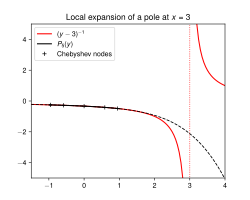
In its simplest form, the fast multipole method seeks to evaluate the following function:

[math]\displaystyle{ f(y) = \sum_{\alpha=1}^N \frac{\phi_\alpha}{y - x_\alpha} }[/math],

where [math]\displaystyle{ x_\alpha \in [-1, 1] }[/math] are a set of poles and [math]\displaystyle{ \phi_\alpha\in\mathbb C }[/math] are the corresponding pole weights on a set of points [math]\displaystyle{ \{y_1,\ldots,y_M\} }[/math] with [math]\displaystyle{ y_\beta \in [-1, 1] }[/math]. This is the one-dimensional form of the problem, but the algorithm can be easily generalized to multiple dimensions and kernels other than [math]\displaystyle{ (y - x)^{-1} }[/math].

Naively, evaluating [math]\displaystyle{ f(y) }[/math] on [math]\displaystyle{ M }[/math] points requires [math]\displaystyle{ \mathcal O(MN) }[/math] operations. The crucial observation behind the fast multipole method is that if the distance between [math]\displaystyle{ y }[/math] and [math]\displaystyle{ x }[/math] is large enough, then [math]\displaystyle{ (y - x)^{-1} }[/math] is well-approximated by a polynomial. Specifically, let [math]\displaystyle{ -1 \lt t_1 \lt \ldots \lt t_p \lt 1 }[/math] be the Chebyshev nodes of order [math]\displaystyle{ p \ge 2 }[/math] and let [math]\displaystyle{ u_1(y), \ldots, u_p(y) }[/math] be the corresponding Lagrange basis polynomials. One can show that the interpolating polynomial:

[math]\displaystyle{ \frac{1}{y-x} = \sum_{i=1}^p \frac{1}{t_i - x} u_i(y) + \epsilon_p(y) }[/math]

converges quickly with polynomial order, [math]\displaystyle{ |\epsilon_{p(y)}| \lt 5^{-p} }[/math], provided that the pole is far enough away from the region of interpolation, [math]\displaystyle{ |x| \ge 3 }[/math] and [math]\displaystyle{ |y| \lt 1 }[/math]. This is known as the "local expansion".

The speed-up of the fast multipole method derives from this interpolation: provided that all the poles are "far away", we evaluate the sum only on the Chebyshev nodes at a cost of [math]\displaystyle{ \mathcal O(N p) }[/math], and then interpolate it onto all the desired points at a cost of [math]\displaystyle{ \mathcal O(M p) }[/math]:

[math]\displaystyle{ \sum_{\alpha=1}^N \frac{\phi_\alpha}{y_\beta - x_\alpha} = \sum_{i=1}^p u_i(y_\beta) \sum_{\alpha=1}^N \frac{1}{t_p - x_\alpha} \phi_\alpha }[/math]

Since [math]\displaystyle{ p = -\log_5\epsilon }[/math], where [math]\displaystyle{ \epsilon }[/math] is the numerical tolerance, the total cost is [math]\displaystyle{ \mathcal O((M + N) \log(1/\epsilon)) }[/math].

To ensure that the poles are indeed well-separated, one recursively subdivides the unit interval such that only [math]\displaystyle{ \mathcal O(p) }[/math] poles end up in each interval. One then uses the explicit formula within each interval and interpolation for all intervals that are well-separated. This does not spoil the scaling, since one needs at most [math]\displaystyle{ \log(1/\epsilon) }[/math] levels within the given tolerance.

See also

• Barnes–Hut simulation
• Multipole expansion
• n-body simulation

External links

• Gibson, Walton C. The Method of Moments in Electromagnetics (3rd ed.), Chapman & Hall/CRC, 2021. ISBN:9780367365066.
• Abstract of Greengard and Rokhlin's original paper
• A short course on fast multipole methods by Rick Beatson and Leslie Greengard.
• JAVA Animation of the Fast Multipole Method Nice animation of the Fast Multipole Method with different adaptations.

Free software

• Puma-EM A high performance, parallelized, open source Method of Moments / Multilevel Fast Multipole Method electromagnetics code.
• KIFMM3d The Kernel-Independent Fast Multipole 3d Method (kifmm3d) is a new FMM implementation which does not require the explicit multipole expansions of the underlying kernel, and it is based on kernel evaluations.
• PVFMM A optimized parallel implementation of KIFMM for computing potentials from particle and volume sources.
• FastBEM Free fast multipole boundary element programs for solving 2D/3D potential, elasticity, stokes flow and acoustic problems.
• FastFieldSolvers maintains the distribution of the tools, called FastHenry and FastCap, developed at M.I.T. for the solution of Maxwell equations and extraction of circuit parasites (inductance and capacitance) using the FMM.
• ExaFMM ExaFMM is a CPU/GPU capable 3D FMM code for Laplace/Helmholtz kernels that focuses on parallel scalability.
• ScalFMM ScalFMM is a C++ software library developed at Inria Bordeaux with high emphasis on genericity and parallelization (using OpenMP/MPI).
• DASHMM DASHMM is a C++ Software library developed at Indiana University using Asynchronous Multi-Tasking HPX-5 runtime system. It provides a unified execution on shared and distributed memory computers and provides 3D Laplace, Yukawa, and Helmholtz kernels.
• RECFMM Adaptive FMM with dynamic parallelism on multicores.