Chebyshev nodes

The Chebyshev nodes are equivalent to the x coordinates of n equally spaced points on a unit semicircle (here, n=10).

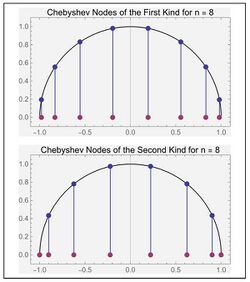
In numerical analysis, Chebyshev nodes are specific real algebraic numbers, namely the roots of the Chebyshev polynomials of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the effect of Runge's phenomenon.

Definition

Zeros of the first 50 Chebyshev polynomials of the first kind

For a given positive integer n the Chebyshev nodes in the interval (−1, 1) are

[math]\displaystyle{ x_k = \cos\left(\frac{2k-1}{2n}\pi\right), \quad k = 1, \ldots, n. }[/math]

These are the roots of the Chebyshev polynomial of the first kind of degree n. For nodes over an arbitrary interval [a, b] an affine transformation can be used:

[math]\displaystyle{ x_k = \frac{1}{2} (a + b) + \frac{1}{2} (b - a) \cos\left(\frac{2k-1}{2n}\pi\right), \quad k = 1, \ldots, n. }[/math]

Approximation

The Chebyshev nodes are important in approximation theory because they form a particularly good set of nodes for polynomial interpolation. Given a function ƒ on the interval [math]\displaystyle{ [-1,+1] }[/math] and [math]\displaystyle{ n }[/math] points [math]\displaystyle{ x_1, x_2, \ldots , x_n, }[/math] in that interval, the interpolation polynomial is that unique polynomial [math]\displaystyle{ P_{n-1} }[/math] of degree at most [math]\displaystyle{ n-1 }[/math] which has value [math]\displaystyle{ f(x_i) }[/math] at each point [math]\displaystyle{ x_i }[/math]. The interpolation error at [math]\displaystyle{ x }[/math] is

[math]\displaystyle{ f(x) - P_{n-1}(x) = \frac{f^{(n)}(\xi)}{n!} \prod_{i=1}^n (x-x_i) }[/math]

for some [math]\displaystyle{ \xi }[/math] (depending on x) in [−1, 1]. So it is logical to try to minimize

[math]\displaystyle{ \max_{x \in [-1,1]} \left| \prod_{i=1}^n (x-x_i) \right|. }[/math]

This product is a monic polynomial of degree n. It may be shown that the maximum absolute value (maximum norm) of any such polynomial is bounded from below by 2¹⁻ⁿ. This bound is attained by the scaled Chebyshev polynomials 2¹⁻ⁿ T_n, which are also monic. (Recall that |T_n(x)| ≤ 1 for x ∈ [−1, 1].) Therefore, when the interpolation nodes x_i are the roots of T_n, the error satisfies

[math]\displaystyle{ \left|f(x) - P_{n-1}(x)\right| \le \frac{1}{2^{n - 1}n!} \max_{\xi \in [-1,1]} \left|f^{(n)} (\xi)\right|. }[/math]

For an arbitrary interval [a, b] a change of variable shows that

[math]\displaystyle{ \left|f(x) - P_{n-1}(x)\right| \le \frac{1}{2^{n - 1}n!} \left(\frac{b-a}{2}\right)^n \max_{\xi \in [a,b]} \left|f^{(n)} (\xi)\right|. }[/math]

References

• Stewart, Gilbert W. (1996), Afternotes on Numerical Analysis, SIAM, ISBN 978-0-89871-362-6 .

Further reading

• Burden, Richard L.; Faires, J. Douglas: Numerical Analysis, 8th ed., pages 503–512, ISBN:0-534-39200-8.