Fish curve

The fish curve with scale parameter a = 1

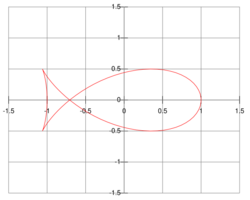
A fish curve is an ellipse negative pedal curve that is shaped like a fish. In a fish curve, the pedal point is at the focus for the special case of the squared eccentricity [math]\displaystyle{ e^2=\tfrac{1}{2} }[/math]. The parametric equations for a fish curve correspond to those of the associated ellipse.

Equations

For an ellipse with the parametric equations

[math]\displaystyle{ \textstyle {x=a\cos(t), \qquad y=\frac {a\sin(t)}{\sqrt {2}}}, }[/math]

the corresponding fish curve has parametric equations

[math]\displaystyle{ \textstyle {x=a\cos(t)-\frac {a\sin^2 (t)}{\sqrt 2}, \qquad y=a\cos(t)\sin(t)}. }[/math]

When the origin is translated to the node (the crossing point), the Cartesian equation can be written as:

[math]\displaystyle{ \left(2x^2+y^2\right)^2-2 \sqrt {2} ax\left(2x^2-3y^2\right)+2a^2\left(y^2-x^2\right)=0. }[/math]

Area

The area of a fish curve is given by:

[math]\displaystyle{ A=\frac {1}{2}\left|\int{\left(xy'-yx'\right)dt}\right| }[/math]

[math]\displaystyle{ =\frac {1}{8}a^2\left|\int{\left[3\cos(t)+\cos(3t)+2\sqrt {2}\sin^2(t)\right]dt}\right| }[/math],

so the area of the tail and head are given by:

[math]\displaystyle{ A_{\mathrm{Tail}}=\left(\frac {2}{3}-\frac {\pi}{4\sqrt {2}}\right)a^2 }[/math]

[math]\displaystyle{ A_{\mathrm{Head}}=\left(\frac {2}{3}+\frac {\pi}{4\sqrt {2}}\right)a^2 }[/math]

giving the overall area for the fish as:

[math]\displaystyle{ A=\frac {4}{3}a^2 }[/math].

Curvature, arc length, and tangential angle

The arc length of the curve is given by [math]\displaystyle{ a\sqrt {2}\left(\frac {1}{2}\pi+3\right) }[/math].

The curvature of a fish curve is given by:

[math]\displaystyle{ K(t)=\frac {2\sqrt {2}+3\cos(t)-\cos(3t)}{2a\left[\cos^4 t+\sin^2 t+\sin^4 t+\sqrt {2}\sin(t)\sin(2t)\right]^\frac {3}{2}} }[/math],

and the tangential angle is given by:

[math]\displaystyle{ \phi(t)=\pi-\arg\left(\sqrt {2}-1-\frac {2}{\left(1+\sqrt {2}\right)e^{it} -1}\right) }[/math]

where [math]\displaystyle{ \arg(z) }[/math] is the complex argument.