Negative pedal curve
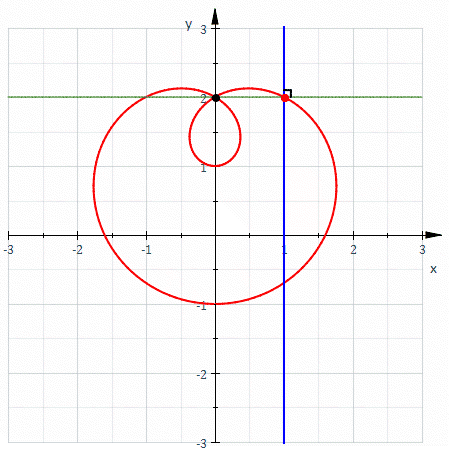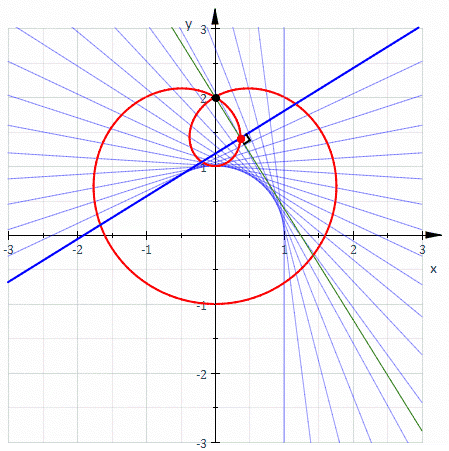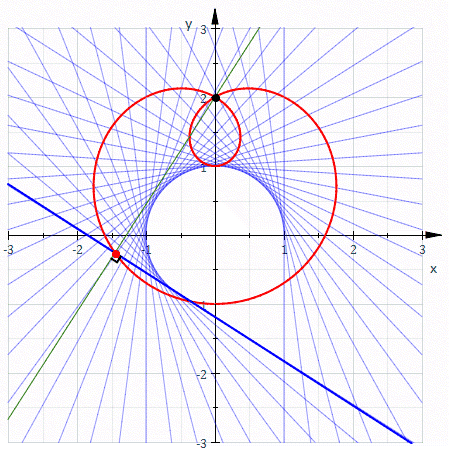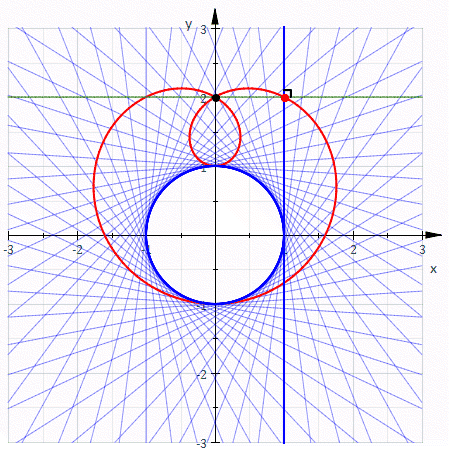
In geometry, a negative pedal curve is a plane curve that can be constructed from another plane curve C and a fixed point P on that curve. For each point X ≠ P on the curve C, the negative pedal curve has a tangent that passes through X and is perpendicular to line XP. Constructing the negative pedal curve is the inverse operation to constructing a pedal curve.
Definition
In the plane, for every point X other than P there is a unique line through X perpendicular to XP. For a given curve in the plane and a given fixed point P, called the pedal point, the negative pedal curve is the envelope of the lines XP for which X lies on the given curve.
Parameterization
For a parametrically defined curve, its negative pedal curve with pedal point (0; 0) is defined as
- [math]\displaystyle{ X[x,y]=\frac{(y^2-x^2)y'+2xyx'}{xy'-yx'} }[/math]
- [math]\displaystyle{ Y[x,y]=\frac{(x^2-y^2)x'+2xyy'}{xy'-yx'} }[/math]
Properties
The negative pedal curve of a pedal curve with the same pedal point is the original curve.
See also
- Fish curve, the negative pedal curve of an ellipse with squared eccentricity 1/2
External links
 |  |
