Fleischner's theorem

From HandWiki
Short description: Theorem on Hamiltonian graphs
A 2-vertex-connected graph, its square, and a Hamiltonian cycle in the square

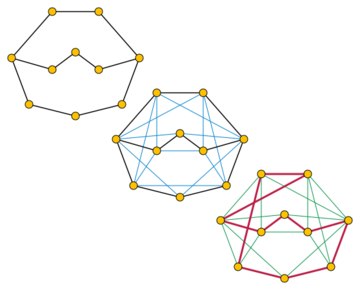
In graph theory, a branch of mathematics, Fleischner's theorem gives a sufficient condition for a graph to contain a Hamiltonian cycle. It states that, if [math]\displaystyle{ G }[/math] is a 2-vertex-connected graph, then the square of [math]\displaystyle{ G }[/math] is Hamiltonian. It is named after Herbert Fleischner, who published its proof in 1974.

Definitions and statement

An undirected graph [math]\displaystyle{ G }[/math] is Hamiltonian if it contains a cycle that touches each of its vertices exactly once. It is 2-vertex-connected if it does not have an articulation vertex, a vertex whose deletion would leave the remaining graph disconnected. Not every 2-vertex-connected graph is Hamiltonian; counterexamples include the Petersen graph and the complete bipartite graph [math]\displaystyle{ K_{2,3} }[/math].

The square of [math]\displaystyle{ G }[/math] is a graph [math]\displaystyle{ G^2 }[/math] that has the same vertex set as [math]\displaystyle{ G }[/math], and in which two vertices are adjacent if and only if they have distance at most two in [math]\displaystyle{ G }[/math]. Fleischner's theorem states that the square of a finite 2-vertex-connected graph with at least three vertices must always be Hamiltonian. Equivalently, the vertices of every 2-vertex-connected graph [math]\displaystyle{ G }[/math] may be arranged into a cyclic order such that adjacent vertices in this order are at distance at most two from each other in [math]\displaystyle{ G }[/math].

Extensions

In Fleischner's theorem, it is possible to constrain the Hamiltonian cycle in [math]\displaystyle{ G^2 }[/math] so that for given vertices [math]\displaystyle{ v }[/math] and [math]\displaystyle{ w }[/math] of [math]\displaystyle{ G }[/math] it includes two edges of [math]\displaystyle{ G }[/math] incident with [math]\displaystyle{ v }[/math] and one edge of [math]\displaystyle{ G }[/math] incident with [math]\displaystyle{ w }[/math]. Moreover, if [math]\displaystyle{ v }[/math] and [math]\displaystyle{ w }[/math] are adjacent in [math]\displaystyle{ G }[/math], then these are three different edges of [math]\displaystyle{ G }[/math].[1]

In addition to having a Hamiltonian cycle, the square of a 2-vertex-connected graph [math]\displaystyle{ G }[/math] must also be Hamiltonian connected (meaning that it has a Hamiltonian path starting and ending at any two designated vertices) and 1-Hamiltonian (meaning that if any vertex is deleted, the remaining graph still has a Hamiltonian cycle).[2] It must also be vertex pancyclic, meaning that for every vertex [math]\displaystyle{ v }[/math] and every integer [math]\displaystyle{ k }[/math] with [math]\displaystyle{ 3\le k\le|V(G) }[/math], there exists a cycle of length [math]\displaystyle{ k }[/math] containing [math]\displaystyle{ v }[/math].[3]

If a graph [math]\displaystyle{ G }[/math] is not 2-vertex-connected, then its square may or may not have a Hamiltonian cycle, and determining whether it does have one is NP-complete.[4]

An infinite graph cannot have a Hamiltonian cycle, because every cycle is finite, but Carsten Thomassen proved that if [math]\displaystyle{ G }[/math] is an infinite locally finite 2-vertex-connected graph with a single end then [math]\displaystyle{ G^2 }[/math] necessarily has a doubly infinite Hamiltonian path.[5] More generally, if [math]\displaystyle{ G }[/math] is locally finite, 2-vertex-connected, and has any number of ends, then [math]\displaystyle{ G^2 }[/math] has a Hamiltonian circle. In a compact topological space formed by viewing the graph as a simplicial complex and adding an extra point at infinity to each of its ends, a Hamiltonian circle is defined to be a subspace that is homeomorphic to a Euclidean circle and covers every vertex.[6]

Algorithms

The Hamiltonian cycle in the square of an [math]\displaystyle{ n }[/math]-vertex 2-connected graph can be found in linear time,[7] improving over the first algorithmic solution by Lau[8] of running time [math]\displaystyle{ O(n^2) }[/math]. Fleischner's theorem can be used to provide a 2-approximation to the bottleneck traveling salesman problem in metric spaces.[9]

History

A proof of Fleischner's theorem was announced by Herbert Fleischner in 1971 and published by him in 1974, solving a 1966 conjecture of Crispin Nash-Williams also made independently by L. W. Beineke and Michael D. Plummer.[10] In his review of Fleischner's paper, Nash-Williams wrote that it had solved "a well known problem which has for several years defeated the ingenuity of other graph-theorists".[11]

Fleischner's original proof was complicated. Václav Chvátal, in the work in which he invented graph toughness, observed that the square of a [math]\displaystyle{ k }[/math]-vertex-connected graph is necessarily [math]\displaystyle{ k }[/math]-tough; he conjectured that 2-tough graphs are Hamiltonian, from which another proof of Fleischner's theorem would have followed.[12] Counterexamples to this conjecture were later discovered,[13] but the possibility that a finite bound on toughness might imply Hamiltonicity remains an important open problem in graph theory. A simpler proof both of Fleischner's theorem, and of its extensions by (Chartrand Hobbs), was given by (Říha 1991),[14] and another simplified proof of the theorem was given by (Georgakopoulos 2009a).[15]

References

Notes

  1. ↑ (Fleischner 1976); (Müttel Rautenbach).
  2. ↑ (Chartrand Hobbs); (Chartrand Lesniak)
  3. ↑ (Hobbs 1976), answering a conjecture of (Bondy 1971).
  4. ↑ (Underground 1978); (Bondy 1995).
  5. ↑ Thomassen (1978).
  6. ↑ (Georgakopoulos 2009b); (Diestel 2012).
  7. ↑ (Alstrup Georgakopoulos)
  8. ↑ (Lau 1980); (Parker Rardin).
  9. ↑ (Parker Rardin); (Hochbaum Shmoys).
  10. ↑ (Fleischner 1974). For the earlier conjectures see Fleischner and (Chartrand Lesniak).
  11. ↑ MR0332573.
  12. ↑ (Chvátal 1973); (Bondy 1995).
  13. ↑ Bauer, Broersma & Veldman (2000).
  14. ↑ (Bondy 1995); (Chartrand Lesniak).
  15. ↑ (Chartrand Lesniak); (Diestel 2012).

Primary sources

Secondary sources



Retrieved from "https://handwiki.org/wiki/index.php?title=Fleischner%27s_theorem&oldid=3385237"