Focus recovery based on the linear canonical transform
Focus recovery from a defocused image is an ill-posed problem since it loses the component of high frequency. Most of the methods for focus recovery are based on depth estimation theory.[1] The Linear canonical transform (LCT) gives a scalable kernel to fit many well-known optical effects. Using LCTs to approximate an optical system for imaging and inverting this system, theoretically permits recovery of a defocused image.
Depth of field and perceptual focus
In photography, depth of field (DOF) means an effective focal length. It is usually used for stressing an object and deemphasizing the background (and/or the foreground). The important measure related to DOF is the lens aperture. Decreasing the diameter of aperture increases focus and lowers resolution and vice versa.
The Huygens–Fresnel principle and DOF
The Huygens–Fresnel principle describes diffraction of wave propagation between two fields. It belongs to Fourier optics rather than geometric optics.The disturbance of diffraction depends on two circumstance parameters, the size of aperture and the interfield distance.
Consider a source field and a destination field, field 1 and field 0, respectively. P1(x1,y1) is the position in the source field, P0(x0,y0) is the position in the destination field. The Huygens–Fresnel principle gives the diffraction formula for two fields U(x0,y0), U(x1,y1) as following:
- [math]\displaystyle{ \mathbf U(x_0,y_0) = \frac{1}{j\lambda}\int\!\int \mathbf U(x_1,y_1) \frac{e^{jkr_{01}}}{r_{01}}\cos\theta dx_1 dy_1 }[/math]
where θ denotes the angle between [math]\displaystyle{ r_{01} }[/math] and [math]\displaystyle{ z }[/math]. Replace cosθ by [math]\displaystyle{ \frac{r_{01}}{z} }[/math] and [math]\displaystyle{ r_{01} }[/math] by
[math]\displaystyle{ [(x_0-x_1)^2+(y_0-y_1)^2+z^2]^{1/2} }[/math]
we get
- [math]\displaystyle{ \mathbf U(x_0,y_0) = \frac{1}{j\lambda z}\int\!\int \mathbf U(x_1,y_1) \frac{\exp(jkz[1+(\frac{x_0-x_1}{z})^2+(\frac{y_0-y_1}{z})^2]^{1/2})}{1+(\frac{x_0-x_1}{z})^2+(\frac{y_0-y_1}{z})^2}dx_1 dy_1 }[/math]
The further distance z or the smaller aperture (x1,y1) causes a greater diffraction. A larger DOF can lead to a more effective focused wave distribution. This seems to be a conflict. Here are the notations:
- Diffraction
- In a real imaging environment, the depths of objects comparing to the aperture are usually not enough to lead to serious diffraction.
- However, a long enough depth of the object can truly blurs the image.
- Effective Focus
- Small aperture, small blurring radius, few wave information.
- Loses details in comparing to a large aperture.
In conclusion, diffraction explains a micro behavior whereas DOF shows a macro behavior. Both of them are related to aperture size.
Linear canonical transform
As the meaning of "canonical", the linear canonical transform (LCT) is a scalable transform that connects to lots of important kernels such as the Fresnel transform, Fraunhofer transform and the fractional Fourier transform. It can be easily controlled by its four parameters, a, b, c, d (3 degrees of freedom). The definition:
- [math]\displaystyle{ L_M(f(u))=\int L_M(u,u')f(u')du' }[/math]
where
- [math]\displaystyle{ L_M(u,u')=\begin{cases} \sqrt\frac{1}{b}e^{-j\pi/4}e^{[j\pi(\frac {d}{b}u^2)-2\frac{1}{b}uu'+\frac{a}{b}u'^2]}, &\mbox{if } b\ne 0 \\ \sqrt{d}e^{\frac{j}{2}cdu^2}\delta(u'-du) ,&\mbox{if } b=0 \end{cases} }[/math]
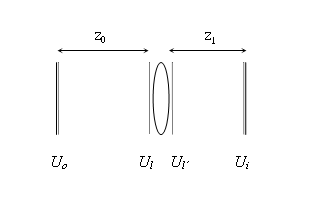
Consider a general imaging system with object distance z0, focal length of the thin lens f and an imaging distance z1. The effect of the propagation in freespace acts as nearly a chirp convolution, that is, the formula of diffraction. Besides, the effect of the propagation in thin lens acts as a chirp multiplication. The parameters are all simplified as paraxial approximations while meeting the freespace propagation. It does not consider aperture size.
From the properties of the LCT, it is possible to obtain those 4 parameters for this optical system as:
- [math]\displaystyle{ \begin{bmatrix} 1-\frac{z_1}{f} \quad &\lambda z_0-\frac{\lambda z_0 z_1}{f}+\lambda z_1 \\ -\frac{1}{\lambda f} \quad &1-\frac{z_0}{f} \end{bmatrix} }[/math]
Once the values of z1, z0 and f are known, the LCT can simulate any optical system.
Notes
- ↑ Most depth recovery methods are simply based on camera focus and defocus. Among those approaches, they usually fall in a depth discontinuity problem.
References
- Haldun M. Ozaktas, Zeev Zalevsky and M. Alper Kutay (2001). The fractional Fourier transform with applications in optics and signal processing. New York: John Wiley & Sons. ISBN 978-0-471-96346-2.
- M. Sorel and J. Flusser, "Space-variant restoration of images degraded by camera motion blur", IEEE Transactions on Image Processing, vol. 17, pp. 105–116, Feb. 2008.
- "The way a zoom lens works". Jos. Schneider Optische Werke GmbH. February 2008. Archived from the original on 2012-05-08. https://web.archive.org/web/20120508065349/http://www.schneiderkreuznach.com/knowhow/zoom_e.htm.
- B. Barshan, M. Alper Kutay and H. M. Ozaktas, "Optimal filtering with linear ca-nonical transformations", Optics Communications, vol. 135, pp. 32–36, Feb. 1997.