Folkman graph

Short description: Bipartite 4-regular graph with 20 nodes and 40 edges

Folkman graph
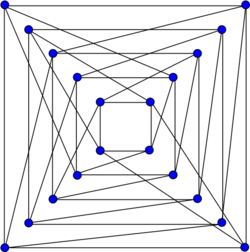Drawing following (Folkman 1967), Figure 1
Named after	Jon Folkman
Vertices	20
Edges	40
Radius	3
Diameter	4
Girth	4
Automorphisms	5! · 25 = 3840
Chromatic number	2
Chromatic index	4
Genus	3
Book thickness	3
Queue number	2
Properties	Bipartite Eulerian Hamiltonian Regular Semi-symmetric
Table of graphs and parameters

In the mathematical field of graph theory, the Folkman graph is a 4-regular graph with 20 vertices and 40 edges. It is a regular bipartite graph with symmetries taking every edge to every other edge, but the two sides of its bipartition are not symmetric with each other, making it the smallest possible semi-symmetric graph. It is named after Jon Folkman, who constructed it for this property in 1967.

The Folkman graph can be constructed either using modular arithmetic or as the subdivided double of the five-vertex complete graph. Beyond the investigation of its symmetry, it has also been investigated as a counterexample for certain questions of graph embedding.

Construction

Semi-symmetric graphs are defined as regular graphs (that is, graphs in which all vertices touch equally many edges) in which each two edges are symmetric to each other, but some two vertices are not symmetric. Jon Folkman was inspired to define and research these graphs in a 1967 paper, after seeing an unpublished manuscript by E. Dauber and Frank Harary which gave examples of graphs meeting the symmetry condition but not the regularity condition. Folkman's original construction of this graph was a special case of a more general construction of semi-symmetric graphs using modular arithmetic, based on a prime number [math]\displaystyle{ p }[/math] congruent to 1 mod 4. For each such prime, there is a number [math]\displaystyle{ r }[/math] such that [math]\displaystyle{ r^2=-1 }[/math] mod [math]\displaystyle{ p }[/math], and Folkman uses modular arithmetic to construct a semi-symmetric graph with [math]\displaystyle{ 2pr }[/math] vertices. The Folkman graph is the result of this construction for [math]\displaystyle{ p=5 }[/math] and [math]\displaystyle{ r=2 }[/math].

Construction of the Folkman graph from the complete graph [math]\displaystyle{ K_5 }[/math]. The green vertices subdivide each edge of [math]\displaystyle{ K_5 }[/math], and the red pairs of vertices are the result of doubling the five vertices of [math]\displaystyle{ K_5 }[/math].

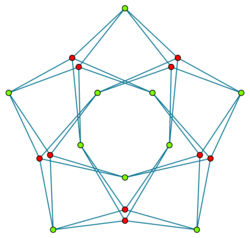
Another construction for the Folkman graph begins with the complete graph on five vertices, [math]\displaystyle{ K_5 }[/math]. A new vertex is placed on each of the ten edges of [math]\displaystyle{ K_5 }[/math], subdividing each edge into a two-edge path. Then, each of the five original vertices of [math]\displaystyle{ K_5 }[/math] is doubled, replacing it by two vertices with the same neighbors. The ten subdivision vertices form one side of the bipartition of the Folkman graph, and the ten vertices in twin pairs coming from the doubled vertices of [math]\displaystyle{ K_5 }[/math] form the other side of the bipartition.

Because each edge of the result comes from a doubled half of an edge of [math]\displaystyle{ K_5 }[/math], and because [math]\displaystyle{ K_5 }[/math] has symmetries taking every half-edge to every other half-edge, the result is edge-transitive. It is not vertex-transitive, because the subdivision vertices are not twins with any other vertex, making them different from the doubled vertices coming from [math]\displaystyle{ K_5 }[/math]. Every 4-regular semi-symmetric graph in which some two vertices have the same neighborhood can be constructed in the same way, by subdividing and then doubling a 4-regular symmetric graph such as [math]\displaystyle{ K_5 }[/math] or the graph of the octahedron. However, there also exist larger 4-regular semi-symmetric graphs that do not have any twin vertices.

Algebraic properties

The automorphism group of the Folkman graph (its group of symmetries) combines the [math]\displaystyle{ 5! }[/math] symmetries of [math]\displaystyle{ K_5 }[/math] with the [math]\displaystyle{ 2^5 }[/math] ways of swapping some pairs of doubled vertices, for a total of [math]\displaystyle{ 5!\cdot 2^5=3840 }[/math] symmetries. This group acts transitively on the Folkman graph's edges (it includes a symmetry taking any edge to any other edge) but not on its vertices. The Folkman graph is the smallest undirected graph that is edge-transitive and regular, but not vertex-transitive. Such graphs are called semi-symmetric graphs and were first studied by Folkman in 1967 who discovered the graph on 20 vertices that now is named after him.

Like all semi-symmetric graphs, the Folkman graph is bipartite. Its automorphism group includes symmetries taking any vertex to any other vertex that is on the same side of the bipartition, but none that take a vertex to the other side of the bipartition. Although one can argue directly that the Folkman graph is not vertex-transitive, this can also be explained group-theoretically: its symmetries act primitively on the vertices constructed as subdivision points of [math]\displaystyle{ K_5 }[/math], but imprimitively on the vertices constructed by doubling the vertices of [math]\displaystyle{ K_5 }[/math]. Every symmetry maps a doubled pair of vertices to another doubled pair of vertices, but there is no grouping of the subdivision vertices that is preserved by the symmetries.

The characteristic polynomial of the Folkman graph is [math]\displaystyle{ (x-4) x^{10} (x+4) (x^2-6)^4 }[/math].

Other properties

The Folkman graph with its vertices arranged in a Hamiltonian cycle. The edges that are not used in this cycle form the second Hamiltonian cycle of a Hamiltonian decomposition.

The Folkman graph has a Hamiltonian cycle, and more strongly a Hamiltonian decomposition into two Hamiltonian cycles. Like every bipartite graph, its chromatic number is two, and its chromatic index (the minimum number of colors needed to color its edges so that no two edges of the same color meet at a vertex) equals its maximum degree, which in this case is four. For instance, such a coloring can be obtained by using two colors in alternation for each cycle of a Hamiltonian decomposition.

Its radius is 3 and its diameter is 4. If [math]\displaystyle{ v }[/math] is one of the doubled vertices of the [math]\displaystyle{ K_5 }[/math] construction, then all other vertices are at most three steps away from [math]\displaystyle{ v }[/math]. However, there are pairs of subdivision vertices from the construction (coming from disjoint edges of [math]\displaystyle{ K_5 }[/math]) that are four steps apart from each other. Because the graph contains many 4-cycles, its girth is 4, the minimum possible for a bipartite graph. It is also 4-vertex-connected and 4-edge-connected. Its treewidth and clique-width are both 5.

The Folkman graph has genus 3: it can be embedded on a triple torus, but not on any simpler oriented surface. It has book thickness 3, but requires five pages for a "dispersable" book embedding in which each page is a matching, disproving a conjecture of Frank Bernhart and Paul Kainen that dispersable book embeddings of regular graphs need only a number of pages equal to their degree.